
20.(本小题满分14分)
已知椭圆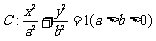 的左、右焦点分别为
的左、右焦点分别为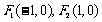 ,且经过点
,且经过点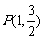 .M为椭圆上的动点,以M为圆心,
.M为椭圆上的动点,以M为圆心,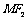 为半径作圆M.
为半径作圆M.
(Ⅰ)求椭圆C的方程;
(Ⅱ)若圆M与y轴有两个交点,求点M横坐标的取值范围;
(Ⅲ)是否存在定圆N,使得圆N与圆M恒相切?若存在,求出圆N的方程;若不存在,请说明理由.
19.(本小题满分14分)
已知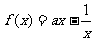 ,
,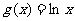 ,
, ,
,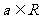 是常数.
是常数.
(Ⅰ)求曲线 在点
在点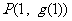 处的切线
处的切线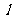 .
.
(Ⅱ)如果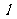 也是曲线
也是曲线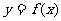 的一条切线,求
的一条切线,求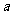 的值;
的值;
(Ⅲ)设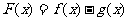 ,讨论函数
,讨论函数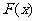 的单调性.
的单调性.
18.(本小题满分14分)
已知四棱锥P-ABCD的三视图如右图。该棱锥中,PA=AB=1,
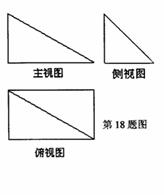 PD与平面ABCD所成角是30°,点F是PB的中点,点E在
PD与平面ABCD所成角是30°,点F是PB的中点,点E在
棱BC上移动.
(I)画出该棱锥的直观图并证明:无论点E在棱BC的何处,总有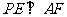 ;
;
(II)连接DE,设G为DE上一动点,当三棱锥P-AGE的体积为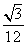 时,试确定G在DE上的位置.
时,试确定G在DE上的位置.
17.(本小题满分12分)
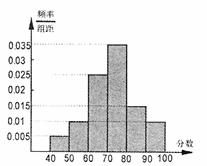 某市教育行政部门为了对2010届高毕业生学业水平进行评价,从该市高中毕业生抽取1000名学生学业水平考试数学成绩为样本进行统计,已知该样本中的每个值都是[40,100]中整数,且在
某市教育行政部门为了对2010届高毕业生学业水平进行评价,从该市高中毕业生抽取1000名学生学业水平考试数学成绩为样本进行统计,已知该样本中的每个值都是[40,100]中整数,且在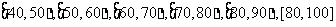 上的频率分布直方图如右图所示。记这1000名学生学业水平考试数学平均成绩的最小可能值为
上的频率分布直方图如右图所示。记这1000名学生学业水平考试数学平均成绩的最小可能值为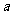 ,最大可能值为
,最大可能值为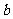 .
.
(I)求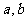 的值;
的值;
(II)从这1000名学生中任取1人,试根据直方图
估计其成绩位于[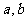 ]中的概率(假设各小组
]中的概率(假设各小组
数据平均分布在相应区间内的所有整数上.)
16.(本小题满分12分)
已知向量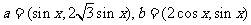 ,定义
,定义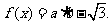
(I)求函数 的单调递减区间;
的单调递减区间;
(II)若函数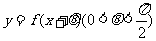 为偶函数,求
为偶函数,求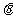 的值.
的值.
(二)选做题(14、15题,考生只能从中选做一题)
14.(坐标系与参数方程选做题)在极坐标系中,过点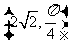 作圆
作圆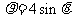 的切线,则切线的极坐标方程是
.
的切线,则切线的极坐标方程是
.
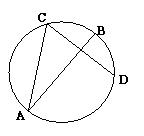
15. (几何证明选讲)如图,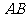 、
、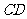 是圆
是圆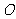 的两条弦,且AB是线段CD的中垂线,已知AB=6,CD=
的两条弦,且AB是线段CD的中垂线,已知AB=6,CD=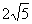 ,则线段AC的长度为 .
,则线段AC的长度为 .
(一)必做题(11-13题)
11.在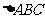 中,
中,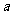 、
、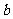 、
、 分别是角A、B、C所对的边,
分别是角A、B、C所对的边,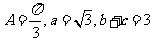 ,则
,则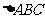 的面积S=
.
的面积S=
.
12.已知P是直线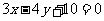 上的动点,PA、PB是圆
上的动点,PA、PB是圆 的两条切线,A、B是切点,C是圆心,那么四边形PACB面积的最小值为 .
的两条切线,A、B是切点,C是圆心,那么四边形PACB面积的最小值为 .
13. 设奇函数
设奇函数 在
在 上是增函数,若
上是增函数,若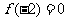 ,则不等式
,则不等式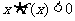 的解集是
.
的解集是
.
10.已知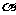 、
、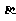 是三次函数
是三次函数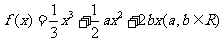 的两个极值点,且
的两个极值点,且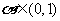 ,
,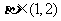 ,则
,则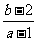 的取值范围是
的取值范围是
A. B.
B. C.
C.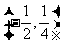 D.
D.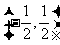
9.等比数列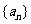 的前
的前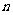 项和为
项和为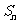 ,若
,若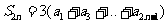 ,
,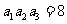 ,则
,则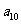 等于
等于
A.-512 B.1024 C.-1024 D.512
8.分别写1,2,3,4的四张卡中随机取出两张,则取出的两张卡片上的数字之和为奇数的概率是
A.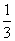 B.
B.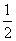 C.
C.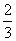 D.
D.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com