
22.(本小题满分14分)
已知函数g(x)=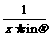 +lnx在[1,+∞)上为增函数,且
+lnx在[1,+∞)上为增函数,且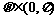 ,f(x)=mx-
,f(x)=mx-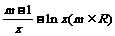
(1)求 的值;¥高#考#资%源*网¥
的值;¥高#考#资%源*网¥
(2)若f(x)-g(x)在[1,+∞)上为单调递增函数,求m的取值范围;
(3)设h(x)=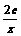 (m>0),若在[1,e]上至少存在一个x0,使得f(x0)-g(x0)>h(x0)成立,求m的取值范围.
(m>0),若在[1,e]上至少存在一个x0,使得f(x0)-g(x0)>h(x0)成立,求m的取值范围.
21.(本小题满分12分)
设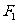 、
、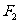 分别是椭圆
分别是椭圆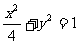 的左、右焦点.
的左、右焦点.
(1)若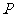 是该椭圆上的一个动点,求向量乘积
是该椭圆上的一个动点,求向量乘积
 的取值范围;
的取值范围;
(2)设过定点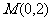 的直线
的直线 与椭圆交于不同的两点M、N,且∠
与椭圆交于不同的两点M、N,且∠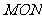 为锐角(其中
为锐角(其中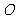 为坐标原点),求直线
为坐标原点),求直线 的斜率
的斜率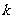 的取值范围. K^S*5U.C#O
的取值范围. K^S*5U.C#O
(3)设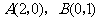 是它的两个顶点,直线
是它的两个顶点,直线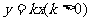 与AB相交于点D,与椭圆相交于E、F两点.求四边形
与AB相交于点D,与椭圆相交于E、F两点.求四边形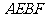 面积的最大值.
面积的最大值.
20.(本小题满分12分)
如图所示,在一条海防警戒线上的点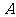 、
、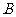 、
、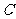 处各有一个水声监测点,
处各有一个水声监测点,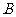 、
、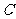 两点到点
两点到点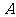 的距离分别为
的距离分别为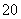 千米和
千米和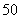 千米.某时刻,
千米.某时刻,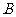 收到发自静止目标
收到发自静止目标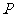 的一个声波信号,8秒后
的一个声波信号,8秒后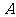 、
、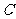 同时接收到该声波信号,已知声波在水中的传播速度是
同时接收到该声波信号,已知声波在水中的传播速度是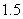 千米/秒.
千米/秒.
(1)设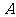 到
到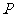 的距离为
的距离为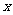 千米,用
千米,用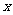 表示
表示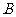 ,
,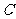 到
到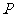 的距离,并求
的距离,并求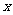 的值;
的值;
(2)求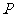 到海防警戒线
到海防警戒线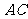 的距离.
的距离.

19.(本小题满分12分)
在数列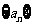 中,
中,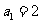 ,
,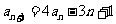 ,
,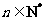 .
.
(1)证明数列 是等比数列;
是等比数列;
(2)设数列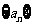 的前
的前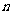 项和
项和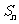 ,求
,求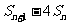 的最大值。
的最大值。
18.(本小题满分12分)
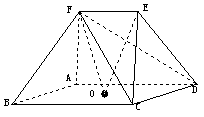 如图,在五面体ABCDEF中,点O是矩形ABCD的对角线的交点,面CDE是等边三角形,棱
如图,在五面体ABCDEF中,点O是矩形ABCD的对角线的交点,面CDE是等边三角形,棱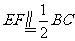

(1)证明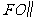 平面
平面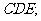
(2)设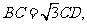 证明
证明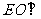 平面
平面
17.(本小题满分12分)
在甲、乙两个盒子中分别装有标号为1、2、3、4的四个球,现从甲、乙两个盒子中各取出1个球,每个小球被取出的可能性相等。K^S*5U.C#O
(1)求取出的两个球上标号为相邻整数的概率;
(2)求取出的两个球上标号之和能被3整除的概率.
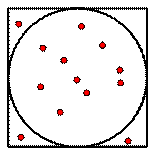
16.小F同学热爱数学,一天,他动手做实验:《用随机模拟的方法估计圆周率的值》,在左下图的正方形中随机撒豆子,每个豆子落在正方形内任何一点是等可能的,他随机地撒50粒,100粒,200粒……分别记录落在圆内的豆子数。若他在撒50粒的实验中统计得到落在圆内的豆子数为35粒,则由此估计出的圆周率 的值为
。(精确到0.01)
的值为
。(精确到0.01)

15.在空间,到定点的距离为定长的点的集合称为球面.定点叫做球心,定长叫做球面 的半径.平面内,以点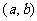 为圆心,以
为圆心,以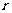 为半径的圆的方程为
为半径的圆的方程为 ,类似的在空间以点
,类似的在空间以点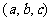 为球心,以
为球心,以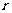 为半径的球面方程为
.
为半径的球面方程为
.
14.已知函数y=f(x)的图象在点M(1,f(1))处的切线方程为y=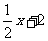 则
则
f(1)+f′(1)= .
13.抛物线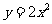 的焦点坐标是________________.¥高#考#资%源*网¥
的焦点坐标是________________.¥高#考#资%源*网¥
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com