
15. A[命题意图]本小题主要考查分类计数原理、组合知识,以及分类讨论的数学思想.
[解析1]:可分以下2种情况:(1)A类选修课选1门,B类选修课选2门,有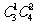 种不同的选法;(2)A类选修课选2门,B类选修课选1门,有
种不同的选法;(2)A类选修课选2门,B类选修课选1门,有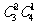 种不同的选法.所以不同的选法共有
种不同的选法.所以不同的选法共有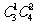 +
+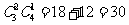 种.
种.
[解析2]: 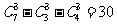
(2010四川文数)(13)(x-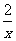 )4的展开式中的常数项为______________(用数字作答)
)4的展开式中的常数项为______________(用数字作答)
解析:展开式的通项公式为Tr+1=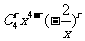
取r=2得常数项为C42(-2)2=24

 w_w w. k#s5_
w_w w. k#s5_
答案:24
14.(2010江西理数)将6位志愿者分成4组,其中两个各2人,另两个组各1人,分赴世博会的四个不同场馆服务,不同的分配方案有 种(用数字作答)。
[答案] 1080
[解析]考查概率、平均分组分配问题等知识,重点考查化归转化和应用知识的意识。先分组,考虑到有2个是平均分组,得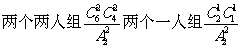 ,再全排列得:
,再全排列得:
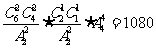
(2010四川理数)(13)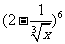 的展开式中的第四项是
. w_w_w.k*s 5*
的展开式中的第四项是
. w_w_w.k*s 5*
解析:T4= w_w_w.k*s 5*
w_w_w.k*s 5*
答案:-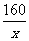
(2010天津理数)(11)甲、乙两人在10天中每天加工零件的个数用茎叶图表示如下图,中间一列的数字表示零件个数的十位数,两边的数字表示零件个数的个位数,则这10天甲、乙两人日加工零件的平均数分别为 和 。
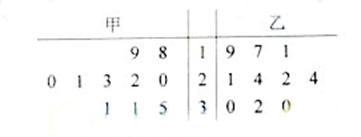
[答案]24,23
[解析]本题主要考查茎叶图的应用,属于容易题。
甲加工零件个数的平均数为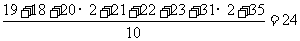
乙加工零件个数的平均数为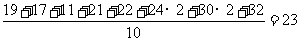
[温馨提示]茎叶图中共同的数字是数字的十位,这事解决本题的突破口。
(2010全国卷1文数)(15)某学校开设A类选修课3门,B类选修课4门,一位同学从中共选3门,若要求两类课程中各至少选一门,则不同的选法共有 种.(用数字作答)
5.(2010上海文数)将一个总数为 、
、 、
、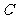 三层,其个体数之比为5:3:2。若用分层抽样方法抽取容量为100的样本,则应从
三层,其个体数之比为5:3:2。若用分层抽样方法抽取容量为100的样本,则应从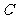 中抽取 20 个个体。
中抽取 20 个个体。
解析:考查分层抽样应从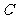 中抽取
中抽取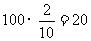
(2010浙江理数)(17)有4位同学在同一天的上、下午参加“身高与体重”、“立定跳远”、“肺活量”、“握力”、“台阶”五个项目的测试,每位同学上、下午各测试一个项目,且不重复. 若上午不测“握力”项目,下午不测“台阶”项目,其余项目上、下午都各测试一人. 则不同的安排方式共有______________种(用数字作答).
解析:本题主要考察了排列与组合的相关知识点,突出对分类讨论思想和数学思维能力的考察,属较难题
(2010全国卷2理数)(14)若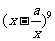 的展开式中
的展开式中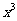 的系数是
的系数是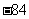 ,则
,则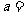 .
.
[答案]1
[命题意图]本试题主要考查二项展开式的通项公式和求指定项系数的方法.
[解析]展开式中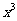 的系数是
的系数是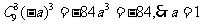 .
.
(2010辽宁理数)(13)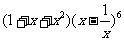 的展开式中的常数项为_________.
的展开式中的常数项为_________.
[答案]-5
[命题立意]本题考查了二项展开式的通项,考查了二项式常数项的求解方法
[解析]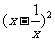 的展开式的通项为
的展开式的通项为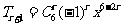 ,当r=3时,
,当r=3时,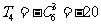 ,当r=4时,
,当r=4时, ,因此常数项为-20+15=-5
,因此常数项为-20+15=-5
(2010全国卷2文数)(14)(x+1/x)9的展开式中,x3的系数是_________
[解析]84:本题考查了二项展开式定理的基础知识
∵  ,∴
,∴ 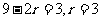 ,∴
,∴ 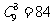
12.(2010上海文数)在 行
行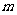 列矩阵
列矩阵 中,
中,
记位于第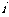 行第
行第 列的数为
列的数为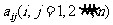 。当
。当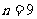 时,
时,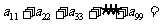 45 。
45 。
解析: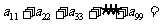 1+3+5+7+9+2+4+6+8=45
1+3+5+7+9+2+4+6+8=45
11.(2010上海文数) 2010年上海世博会园区每天9:00开园,20:00停止入园。在右边的框图中,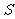 表示上海世博会官方网站在每个整点报道的入园总人数,
表示上海世博会官方网站在每个整点报道的入园总人数,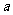 表示整点报道前1个小时内入园人数,则空白的执行框内应填入 S←S+a 。
表示整点报道前1个小时内入园人数,则空白的执行框内应填入 S←S+a 。
解析:考查算法
8.[答案]B
[解析]分类讨论:若有2人从事司机工作,则方案有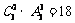 ;若有1人从事司机工作,则方案有
;若有1人从事司机工作,则方案有 种,所以共有18+108=126种,故B正确
种,所以共有18+108=126种,故B正确
8、(2010湖北理数)现安排甲、乙、丙、丁、戌5名同学参加上海世博会志愿者服务活动,每人从事翻译、导游、礼仪、司机四项工作之一,每项工作至少有一人参加。甲、乙不会开车但能从事其他三项工作,丙丁戌都能胜任四项工作,则不同安排方案的种数是
A.152 B.126 C.90 D.54
7、(2010湖南理数)在某种信息传输过程中,用4个数字的一个排列(数字允许重复)表示一个信息,不同排列表示不同信息,若所用数字只有0和1,则与信息0110至多有两个对应位置上的数字相同的信息个数为
A.10 B.11 C.12 D.15

6.(2010湖北文数)现有名同学支听同时进行的个课外知识讲座,名每同学可自由选择其中的一个讲座,不同选法的种数是
A.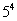 B.
B.
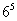 C.
C.
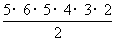 D.
D.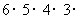
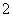

5.A. [命题意图]本小题主要考查了考生对二项式定理的掌握情况,尤其是展开式的通项公式的灵活应用,以及能否区分展开式中项的系数与其二项式系数,同时也考查了考生的一些基本运算能力.
[解析]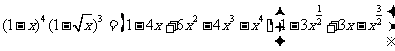
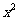 的系数是 -12+6=-6
的系数是 -12+6=-6
(2010全国卷1理数)(6)某校开设A类选修课3门,B类选择课4门,一位同学从中共选3门.若要求两类课程中各至少选一门,则不同的选法共有
(A) 30种 (B)35种 (C)42种 (D)48种

(2010全国卷1理数)(5)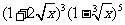 的展开式中x的系数是
的展开式中x的系数是
(A) -4 (B) -2 (C) 2 (D) 4

(2010四川文数)(9)由1、2、3、4、5组成没有重复数字且1、2都不与5相邻的五位数的个数是
(A)36 (B)32 (C)28 (D)24
解析:如果5在两端,则1、2有三个位置可选,排法为2×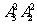 =24种
=24种
如果5不在两端,则1、2只有两个位置可选,3×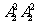 =12种
=12种
共计12+24=36种
答案:A

 w_w w. k#s5_
w_w w. k#s5_
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com