
(9)在复平面内,复数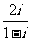 对应的点的坐标为
。
对应的点的坐标为
。
9,(-1,1).
解析: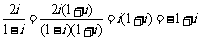
(10)在△ABC中,若b = 1,c = ,
,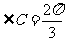 ,则a =
。
,则a =
。
10, 1。
解析: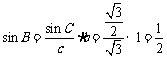 ,因此
,因此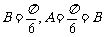 ,故
,故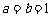
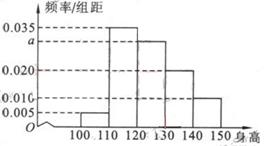 (11)从某小学随机抽取100名同学,将他们的身高(单位:厘米)数据绘制成频率分布直方图(如图)。由图中数据可知a=
。若要从身高在[ 120 , 130),[130 ,140) , [140 , 150]三组内的学生中,用分层抽样的方法选取18人参加一项活动,则从身高在[140 ,150]内的学生中选取的人数应为
。
(11)从某小学随机抽取100名同学,将他们的身高(单位:厘米)数据绘制成频率分布直方图(如图)。由图中数据可知a=
。若要从身高在[ 120 , 130),[130 ,140) , [140 , 150]三组内的学生中,用分层抽样的方法选取18人参加一项活动,则从身高在[140 ,150]内的学生中选取的人数应为
。
11,0.030, 3
解析:由所有小矩形面积为1不难得到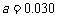 ,而三组身高区间的人数比为3:2:1,由分层抽样的原理不难得到140-150区间内的人数为3人。
,而三组身高区间的人数比为3:2:1,由分层抽样的原理不难得到140-150区间内的人数为3人。
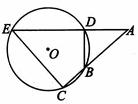
(12)如图, 的弦ED,CB的延长线交于点A。若BD
的弦ED,CB的延长线交于点A。若BD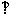 AE,AB=4, BC=2, AD=3,则DE=
;CE=
。
AE,AB=4, BC=2, AD=3,则DE=
;CE=
。
12,5,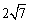
解析:首先由割线定理不难知道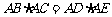 ,于是
,于是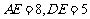 ,又
,又 ,故
,故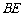 为直径,因此
为直径,因此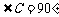 ,由勾股定理可知
,由勾股定理可知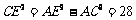 ,故
,故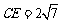
(13)已知双曲线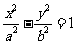 的离心率为2,焦点与椭圆
的离心率为2,焦点与椭圆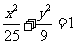 的焦点相同,那么双曲线的焦点坐标为 ;渐近线方程为
。
的焦点相同,那么双曲线的焦点坐标为 ;渐近线方程为
。
13,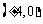 ,
,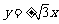
解析:双曲线焦点即为椭圆焦点,不难算出为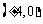 ,又双曲线离心率为2,即
,又双曲线离心率为2,即 ,故
,故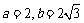 ,渐近线为
,渐近线为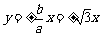
 (14)如图放置的边长为1的正方形PABC沿
(14)如图放置的边长为1的正方形PABC沿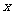 轴滚动。
轴滚动。
设顶点P(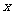 ,y)的轨迹方程是
,y)的轨迹方程是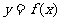 ,则
,则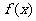 的最小正周期为
;
的最小正周期为
;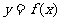 在其两个相邻零点间的图像与
在其两个相邻零点间的图像与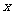 轴
轴
所围区域的面积为 。
说明:“正方形PABC沿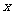 轴滚动”包括沿
轴滚动”包括沿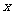 轴正方向和沿
轴正方向和沿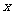 轴负方向滚动。沿
轴负方向滚动。沿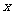 轴正方向滚动指的是先以顶点A为中心顺时针旋转,当顶点B落在
轴正方向滚动指的是先以顶点A为中心顺时针旋转,当顶点B落在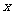 轴上时,再以顶点B为中心顺时针旋转,如此继续。类似地,正方形PABC可以沿
轴上时,再以顶点B为中心顺时针旋转,如此继续。类似地,正方形PABC可以沿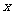 轴负方向滚动。
轴负方向滚动。
14, 4,
解析:不难想象,从某一个顶点(比如A)落在x轴上的时候开始计算,到下一次A点落在x轴上,这个过程中四个顶点依次落在了x轴上,而每两个顶点间距离为正方形的边长1,因此该函数的周期为4。下面考察P点的运动轨迹,不妨考察正方形向右滚动,P点从x轴上开始运动的时候,首先是围绕A点运动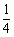 个圆,该圆半径为1,然后以B点为中心,滚动到C点落地,其间是以BP为半径,旋转90°,然后以C为圆心,再旋转90°,这时候以CP为半径,因此最终构成图象如下:
个圆,该圆半径为1,然后以B点为中心,滚动到C点落地,其间是以BP为半径,旋转90°,然后以C为圆心,再旋转90°,这时候以CP为半径,因此最终构成图象如下:
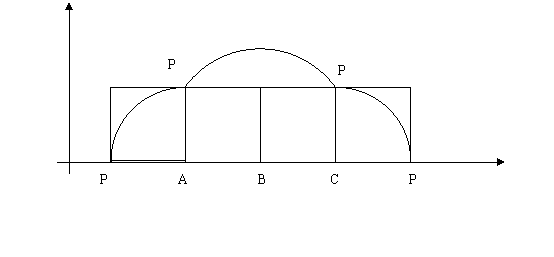

因此不难算出这块的面积为
(1) 集合 ,则
,则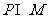 =
=
(A) {1,2} (B) {0,1,2} (C){x|0≤x<3} (D) {x|0≤x≤3}
1,B.
解析: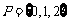 ,
,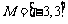 ,因此
,因此
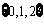
(2)在等比数列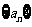 中,
中,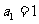 ,公比
,公比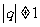 .若
.若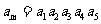 ,则m=
,则m=
 (A)9 (B)10 (C)11
(D)12
(A)9 (B)10 (C)11
(D)12
2,C.
解析: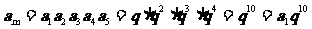 ,因此有
,因此有
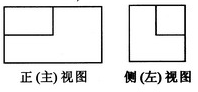
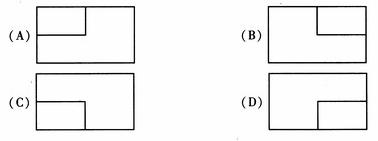
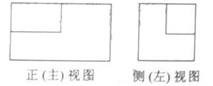
(3)一个长方体去掉一个小长方体,所得几何体的正(主)视图与侧(左)视图分别如右图所示,则该几何体的俯视图为
3,C.
解析:很容易看出这是一个面向我们的左上角缺了一小块长方体的图形,不难选出答案。
(4)8名学生和2位第师站成一排合影,2位老师不相邻的排法种数为
(A)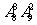 (B)
(B)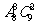 (C)
(C)
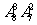 (D)
(D)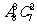
4,A.
解析:基本的插空法解决的排列组合问题,将所有学生先排列,有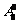 种排法,然后将两位老师插入9个空中,共有
种排法,然后将两位老师插入9个空中,共有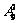 种排法,因此一共有
种排法,因此一共有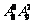 种排法。
种排法。
(5)极坐标方程( -1)(
-1)( )=0(
)=0(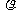
 0)表示的图形是
0)表示的图形是
(A)两个圆 (B)两条直线
(C)一个圆和一条射线 (D)一条直线和一条射线
5,C.
解析:原方程等价于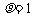 或
或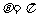 ,前者是半径为1的圆,后者是一条射线。
,前者是半径为1的圆,后者是一条射线。
(6)若 ,
,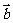 是非零向量,“
是非零向量,“ ⊥
⊥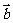 ”是“函数
”是“函数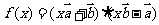 为一次函数”的
为一次函数”的
(A)充分而不必要条件 (B)必要不充分条件
(C)充分必要条件 (D)既不充分也不必要条件
6,B.
解析: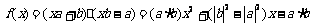 ,如
,如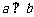 ,则有
,则有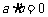 ,如果同时有
,如果同时有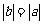 ,则函数恒为0,不是一次函数,因此不充分,而如果
,则函数恒为0,不是一次函数,因此不充分,而如果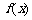 为一次函数,则
为一次函数,则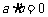 ,因此可得
,因此可得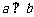 ,故该条件必要。
,故该条件必要。
(7)设不等式组 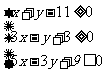 表示的平面区域为D,若指数函数y=
表示的平面区域为D,若指数函数y= 的图像上
的图像上
存在区域D上的点,则a 的取值范围是
(A)(1,3]
(B )[2,3] (C )
(1,2]
(D )[ 3,  ]
]
7,A.
解析:这是一道略微灵活的线性规划问题,作出区域D的图象,联系指数函数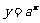 的图象,能够看出,当图象经过区域的边界点(2,9)时,a可以取到最大值3,而显然只要a大于1,图象必然经过区域内的点。
的图象,能够看出,当图象经过区域的边界点(2,9)时,a可以取到最大值3,而显然只要a大于1,图象必然经过区域内的点。
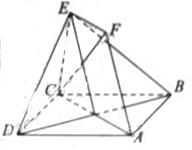
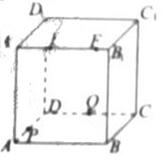
 (8)如图,正方体ABCD-
(8)如图,正方体ABCD-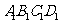 的棱长为2,动点E、F在棱
的棱长为2,动点E、F在棱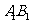 上,动点P,Q分别在棱AD,CD上,若EF=1,
上,动点P,Q分别在棱AD,CD上,若EF=1,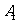 E=x,DQ=y,DP=z(x,y,z大于零),则四面体PEFQ的体积
E=x,DQ=y,DP=z(x,y,z大于零),则四面体PEFQ的体积
(A)与x,y,z都有关
(B)与x有关,与y,z无关
(C)与y有关,与x,z无关
(D)与z有关,与x,y无关
8,D.
解析:这道题目延续了北京高考近年8,14,20的风格,即在变化中寻找不变,从图中可以分析出,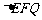 的面积永远不变,为面
的面积永远不变,为面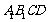 面积的
面积的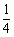 ,而当
,而当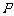 点变化时,它到面
点变化时,它到面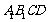 的距离是变化的,因此会导致四面体体积的变化。
的距离是变化的,因此会导致四面体体积的变化。
第II卷(共110分)
(15)(本小题共13分)
 已知函数
已知函数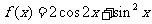
(Ⅰ)求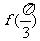 的值;
的值;
(Ⅱ)求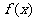 的最大值和最小值
的最大值和最小值

 (16)(本小题共13分)
(16)(本小题共13分)
已知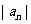 为等差数列,且
为等差数列,且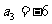 ,
,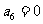 。
。
(Ⅰ)求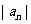 的通项公式;
的通项公式;
(Ⅱ)若等差数列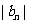 满足
满足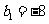 ,
,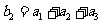 ,求
,求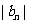 的前n项和公式
的前n项和公式
⒃ 答案(共13分)

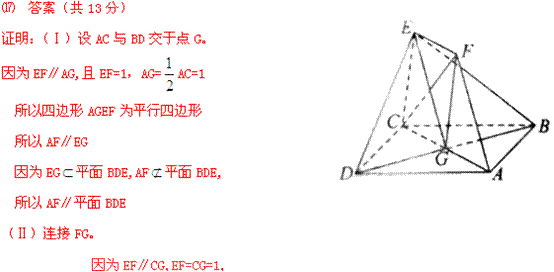
 (17)(本小题共13分)
(17)(本小题共13分)
如图,正方形ABCD和四边形ACEF所在的平面互相垂直。
 EF//AC,AB=
EF//AC,AB=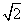 ,CE=EF=1
,CE=EF=1
(Ⅰ)求证:AF//平面BDE;
(Ⅱ)求证:CF⊥平面BDF;



(18) (本小题共14分)
设定函数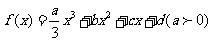 ,且方程
,且方程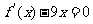 的两个根分别为1,4。
的两个根分别为1,4。
(Ⅰ)当a=3且曲线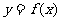 过原点时,求
过原点时,求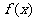 的解析式;
的解析式;
(Ⅱ)若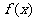 在
在 无极值点,求a的取值范围。
无极值点,求a的取值范围。



 (19)(本小题共14分)
(19)(本小题共14分)
已知椭圆C的左、右焦点坐标分别是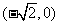 ,
,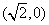 ,离心率是
,离心率是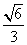 ,直线y=t椭圆C交与不同的两点M,N,以线段MN为直径作圆P,圆心为P。
,直线y=t椭圆C交与不同的两点M,N,以线段MN为直径作圆P,圆心为P。
(Ⅰ)求椭圆C的方程;
(Ⅱ)若圆P与x轴相切,求圆心P的坐标;
(Ⅲ)设Q(x,y)是圆P上的动点,当t变化时,求y的最大值。
(19)答案(共14分)
解:(Ⅰ)因为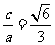 ,且
,且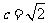 ,
,
所以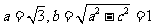
所以椭圆C的方程为


19.[命题意图]本题考查了椭圆方程、直线与圆的位置关系以及应用参数法求最值等问题.问题的设置由浅入深,符合学生的思维能力的生成过程,问题的设置也兼顾考查了应用代数的思想解决几何问题的能力.
[点评]圆锥曲线问题是每年的必考题型,其试题的难度会有所增加,但是其试题一般都是有梯度的,且此类问题的设置时基于对基础知识、基本能力的考查基础上能力的拔高.求解此类问题往往要应用到代数的方法和思想来求解,故此在平时的学习中要注意对圆锥曲线的标准方程、参数关系、基本方法、基本题型的掌握和熟练.
(20)(本小题共13分)
已知集合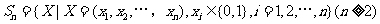 对于
对于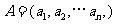 ,
, ,定义A与B的差为
,定义A与B的差为
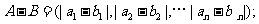
A与B之间的距离为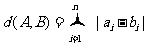
(Ⅰ)当n=5时,设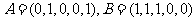 ,求
,求 ,
,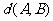 ;
;
(Ⅱ)证明: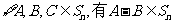 ,且
,且 ;
;
(Ⅲ) 证明: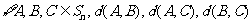 三个数中至少有一个是偶数
三个数中至少有一个是偶数
(20)答案(共13分)
(Ⅰ)解: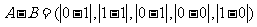 =(1,0,1,0,1)
=(1,0,1,0,1)


设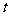 是使
是使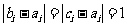 成立的
成立的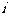 的个数。则
的个数。则


(9)已知函数 右图表示的是给
右图表示的是给
定x的值,求其对应的函数值y的程序框图,
①处应填写 ;②处应填写 。

 (10)在
(10)在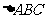 中。若
中。若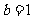 ,
,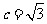 ,
,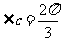 ,则a= 。
,则a= 。

 (11)若点p(m,3)到直线
(11)若点p(m,3)到直线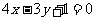 的距离为4,且点p在不等式
的距离为4,且点p在不等式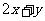 <3表示的平面区域内,则m=
。
<3表示的平面区域内,则m=
。

 (12)从某小学随机抽取100名同学,将他们身高
(12)从某小学随机抽取100名同学,将他们身高
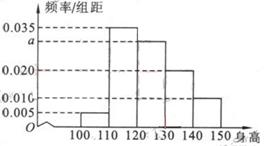 (单位:厘米)数据绘制成频率分布直方图(如图)。
(单位:厘米)数据绘制成频率分布直方图(如图)。
由图中数据可知a= 。若要从身高在
[120,130﹚,[130,140﹚,[140,150]三组内的
学生中,用分层抽样的方法选取18人参加一项活动
,则从身高在[140,150]内的学生中选取的人数
应为 。

 所以在身高在[140,150]范围内抽取的学生人数为
所以在身高在[140,150]范围内抽取的学生人数为 人.
人.
(13)已知双曲线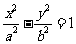 的离心率为2,焦点与椭圆
的离心率为2,焦点与椭圆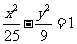 的焦点相同,那么双曲线的焦点坐标为
;渐近线方程为
。
的焦点相同,那么双曲线的焦点坐标为
;渐近线方程为
。
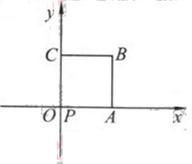

 (14)如图放置的边长为1的正方形PABC沿x轴滚动。
(14)如图放置的边长为1的正方形PABC沿x轴滚动。
设顶点p(x,y)的纵坐标与横坐标的函数关系是
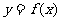 ,则
,则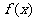 的最小正周期为
;
的最小正周期为
;
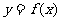 在其两个相邻零点间的图像与x轴
在其两个相邻零点间的图像与x轴
所围区域的面积为 。
说明:“正方形PABC沿x轴滚动”包含沿x轴正方向和沿x轴负方向滚动。沿x轴正方向滚动是指以顶点A为中心顺时针旋转,当顶点B落在x轴上时,再以顶点B为中心顺时针旋转,如此继续,类似地,正方形PABC可以沿着x轴负方向滚动。


⑴ 集合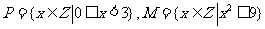 ,则
,则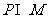 =
=
(A) {1,2} (B) {0,1,2} (C){1,2,3} (D){0,1,2,3}

⑵在复平面内,复数6+5i, -2+3i 对应的点分别为A,B.若C为线段AB的中点,则点C对应的复数是
(A)4+8i (B)8+2i (C)2+4i (D)4+i
(2)答案C
[命题意图]本题考查复平面的基本知识及中点坐标公式.求解此类问题要能够灵活准确的对复平面内的点的坐标与复数进行相互转化.
[解析]两个复数对应的点的坐标分别为A(6,5),B(-2,3),则其中点的坐标为C(2,4),故
其对应的复数为2+4i.
⑶从{1,2,3,4,5}中随机选取一个数为a,从{1,2,3}中随机选取一个数为b,则b>a的概率是
(A)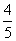 (B)
(B)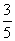 (C)
(C) (D)
(D)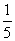
 ⑷若a,b是非零向量,且
⑷若a,b是非零向量,且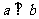 ,
,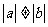 ,则函数
,则函数 是
是
(A)一次函数且是奇函数 (B)一次函数但不是奇函数
(C)二次函数且是偶函数 (D)二次函数但不是偶函数

 (5)一个长方体去掉一个小长方体,所得几何体的
(5)一个长方体去掉一个小长方体,所得几何体的
正视图与侧(左)视图分别如右图所示,则该集合体
的俯视图为:
 (6)给定函数①
(6)给定函数①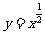 ,②
,②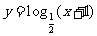 ,③
,③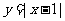 ,④
,④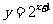 ,期中在区间(0,1)上单调递减的函数序号是
,期中在区间(0,1)上单调递减的函数序号是
(A)①② (B)②③ (C)③④ (D)①④


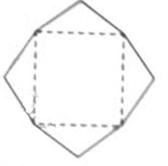 (7)某班设计了一个八边形的班徽(如图),它由腰长为1,
(7)某班设计了一个八边形的班徽(如图),它由腰长为1,
顶角为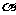 的四个等腰三角形,及其底边构成的正方形所组成,
的四个等腰三角形,及其底边构成的正方形所组成,
该八边形的面积为
(A)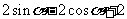 ;
(B)
;
(B)
(C)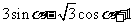 (D)
(D)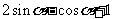
7. 答案A
[命题意图]本题考查了三角面积公式的应用和余弦定理的应用
 (8)如图,正方体
(8)如图,正方体 的棱长为2,
的棱长为2,
动点E、F在棱 上。点Q是CD的中点,动点
上。点Q是CD的中点,动点
P在棱AD上,若EF=1,DP=x,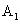 E=y(x,y大于零),
E=y(x,y大于零),
则三棱锥P-EFQ的体积:
(A)与x,y都有关; (B)与x,y都无关;
(C)与x有关,与y无关; (D)与y有关,与x无关;

 第Ⅱ卷(共110分)
第Ⅱ卷(共110分)
22、 1959年,美国国家展览会在莫斯科举办。对于榨汁机和洗碗机等展品。赫鲁晓夫表示工人阶级决不会购买这些无用的小器具,当场引起了美国副总统尼克松的反对。这反映了当时 A . 美苏冷战的重点从军事领域转向经济领域 B . 美国霸主地位动摇,急需打开苏联市场 C . 苏联轻工业发达,不需要进口这些器具 D . 经济文化交流没有改变两国意识形态的对立
题眼:时间“1959年”,“榨汁机和洗碗机等展品”,“赫鲁晓夫表示……尼克松的反对。”
考点:冷战时期的苏美历史状况
解析:1959年,正值美苏争霸时期,从材料中两位总统的言辞可以看出,展览会上经济文

19、“我们不把任何未经验证的意见接受作为真理,而是遵照必要的次序,从一步推演到下一步……不论多么深奥,最终都能发现。”与这句话的理念一致的说法是
A. “信仰即可得救”
 21、《新编剑桥世界近代史》中有这样的评述:“两个学说都发现了变化的原因在于斗争--生存竞争和阶级斗争。”这两个学说最终形成于
A. 17世纪初期 B.18世纪中期 C.19世纪中期
D.20世纪初期
21、《新编剑桥世界近代史》中有这样的评述:“两个学说都发现了变化的原因在于斗争--生存竞争和阶级斗争。”这两个学说最终形成于
A. 17世纪初期 B.18世纪中期 C.19世纪中期
D.20世纪初期
题眼:生存竞争和阶级斗争(学说)。
考点:马克思主义学说与达尔文进化论
解析:阐述“生存竞争和阶级斗争”的两个学说分别是1859年《物种起源》和1848年《共产党宣言》的发表。因此这两个学说最终形成于19世纪中期。
答案:C。
18、下表是我国某时期的国际邮件资费表(部分),从中可推出的符合史实的结论是
|
邮件种类 |
计费单位(每10克) |
邮资(元) |
|
航空 |
亚洲各国 |
0.32[ |
|
苏联及东欧民主国家 |
0.48 |
|
|
西欧各国(捷克转) |
0.48 |
|
|
西欧各国(香港转) |
0.80 |
|
|
其他各洲 |
0.80 |
A.香港已经回归,成为中国与西欧交往的重要桥梁 B.改革开放前,中国没有与西方国家建立外交关系 C.捷克已加入欧盟,成为中国往西欧各国邮件的中转地 D.新中国外交史上,苏联及东欧民主国家曾有特殊地位
题眼:国际邮件资费表数据
考点:新中国外交
解析:从国际邮件资费表可以看出,该时段为两大阵营对峙(冷战)时期,新中国外交史上,苏联及东欧民主国家曾有特殊地位。香港1997年回归,A说法不正确;B项明显可以排除;捷克2005年才加入欧盟,C不正确。
答案:D。
13.北魏均田制实行后,文献中出现了“庄园”一词,被指圈占的成片土地。唐代均田制实行后,“庄园”一词的使用更普遍。这反映了均田制实行后 A.井田制得以恢复 B.不存在土地私有现象 C.仍存在土地集中现象 D.庄园由中央集中管理
题眼:均田制实行后,“庄园”一次的使用更普遍的原因。
考点:均田制与“庄园”的关系--土地兼并
解析:庄园是一个自给自足程度相当高的经济、政治、文化单位。 唐代均田制实行后,“庄园”一词的使用更普遍。这反映了均田制实行后,地主依旧圈占的成片土地,存在土地集中现象。
答案:C.


湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com