
7.设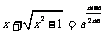 ,求
,求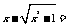 .
.
6.计算.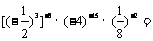 .
.
5.设函数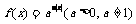 ,f(2)=4,则( )
,f(2)=4,则( )
A.f(-2)>f(-1) B.f(-1)>f(-2) C.f(1)>f(2) D.f(-2)>f(2)
4.把函数y=f(x)的图象向左、向下分别平移2个单位长度,得到函数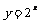 的图象,则( )
的图象,则( )
A.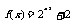 B.
B.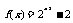 C.
C. D.
D.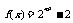
3.下列函数中,图象与函数y=4x的图象关于y轴对称的是( )
A.y=-4x B.y=4-x C.y=-4-x D.y=4x+4-x
2.要使代数式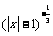 有意义,则x的取值范围是( )
有意义,则x的取值范围是( )
A.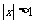 B.
B.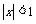 C.
C.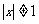 D.一切实数
D.一切实数
1.数 的大小关系是( )
的大小关系是( )
A.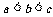 B.
B.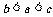 C.
C.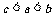 D.
D.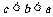
20.记函数f(x)的定义域为D,若存在x0∈D,使f(x0)=x0成立,则称以(x0,y0)为坐标的点是函数f(x)的图象上的“稳定点”.
(1)若函数f(x)=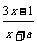 的图象上有且只有两个相异的“稳定点”,试求实数a的取值范围;
的图象上有且只有两个相异的“稳定点”,试求实数a的取值范围;
(2)已知定义在实数集R上的奇函数f(x)存在有限个“稳定点”,求证:f(x)必有奇数个“稳定点”.
 必修1
第2章 函数概念与基本初等函数Ⅰ
必修1
第2章 函数概念与基本初等函数Ⅰ
§2.2指数函数
重难点:对分数指数幂的含义的理解,学会根式与分数指数幂的互化并掌握有理指数幂的运算性质;指数函数的性质的理解与应用,能将讨论复杂函数的单调性、奇偶性问题转化为讨论比较简单的函数的有关问题.
考纲要求:①了解指数函数模型的实际背景;
②理解有理指数幂的含义,了解实数指数幂的意义,掌握幂的运算;
③理解指数函数的概念,并理解指数函数的单调性与函数图像通过的特殊点;
④知道指数函数是一类重要的函数模型.
经典例题:求函数y=3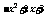 的单调区间和值域.
的单调区间和值域.
当堂练习:
19.定义在(-1,1)上的函数f(x)满足:对任意x、y∈(-1,1)都有f(x)+f(y)=f(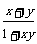 ).
).
(1)求证:函数f(x)是奇函数;
(2)如果当x∈(-1,0)时,有f(x)>0,求证:f(x)在(-1,1)上是单调递减函数;
18.定义在R上的函数f(x)满足:如果对任意x1,x2∈R,都有f(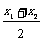 )≤
)≤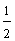 [f(x1)+f(x2)],则称函数f(x)是R上的凹函数.已知函数f(x)=ax2+x(a∈R且a≠0),求证:当a>0时,函数f(x)是凹函数;
[f(x1)+f(x2)],则称函数f(x)是R上的凹函数.已知函数f(x)=ax2+x(a∈R且a≠0),求证:当a>0时,函数f(x)是凹函数;
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com