
3.函数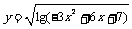 的值域是( )
的值域是( )
A.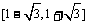 B.[0,1] C.[0,
B.[0,1] C.[0, D.{0}
D.{0}
2.设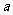 表示
表示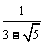 的小数部分,则
的小数部分,则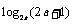 的值是( )
的值是( )
A.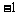 B.
B.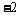 C.0 D.
C.0 D.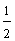
1.若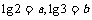 ,则
,则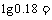 ( )
( )
A.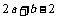 B.
B.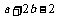 C.
C.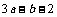 D.
D.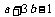
14.已知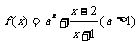
(1)证明函数f(x)在 上为增函数;(2)证明方程
上为增函数;(2)证明方程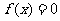 没有负数解.
没有负数解.
 必修1
第2章 函数概念与基本初等函数Ⅰ
必修1
第2章 函数概念与基本初等函数Ⅰ
§2.3对数函数
重难点:理解并掌握对数的概念以及对数式和指数式的相互转化,能应用对数运算性质及换底公式灵活地求值、化简;理解对数函数的定义、图象和性质,能利用对数函数单调性比较同底对数大小,了解对数函数的特性以及函数的通性在解决有关问题中的灵活应用.
考纲要求:①理解对数的概念及其运算性质,知道用换底公式能将一般对数转化成自然对数或常用对数;了解对数在简化运算中的作用;
②理解对数函数的概念;理解对数函数的单调性,掌握函数图像通过的特殊点;
③知道对数函数是一类重要的函数模型;
④了解指数函数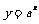 与对数函数
与对数函数 互为反函数
互为反函数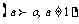 .
.
经典例题:已知f(logax)=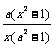 ,其中a>0,且a≠1.
,其中a>0,且a≠1.
(1)求f(x); (2)求证:f(x)是奇函数; (3)求证:f(x)在R上为增函数.
当堂练习:
13.求下列函数的单调区间及值域:
(1)  ; (2)
; (2)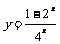 ; (3)求函数
; (3)求函数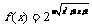 的递增区间.
的递增区间.
12.(1)已知x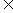 [-3,2],求f(x)=
[-3,2],求f(x)=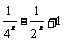 的最小值与最大值.
的最小值与最大值.
(2)已知函数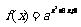 在[0,2]上有最大值8,求正数a的值.
在[0,2]上有最大值8,求正数a的值.
(3)已知函数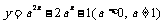 在区间[-1,1]上的最大值是14,求a的值.
在区间[-1,1]上的最大值是14,求a的值.
11.先化简,再求值: (1)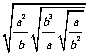 ,其中
,其中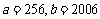 ;
;
(2) 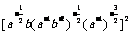 ,其中
,其中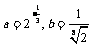 .
.
10.若函数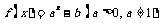 的图象不经过第二象限,则
的图象不经过第二象限,则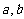 满足的条件是
.
满足的条件是
.
9.函数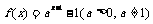 的图象恒过定点
.
的图象恒过定点
.
8.已知 是奇函数,则
是奇函数,则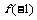 =
.
=
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com