
5.如果把函数y=f(x)在x=a及x=b之间的一段图象近似的看作直线的一段,设a≤c≤b,那么f(c)的近似值可表示为( )
A.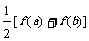 B.
B.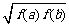 C.f(a)+
C.f(a)+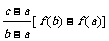 D.f(a)-
D.f(a)-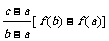
4. 设方程2x+2x=10的根为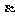 ,则
,则 ( )
( )
A.(0,1) B.(1,2) C.(2,3) D.(3,4)
3.对于任意k∈[-1,1],函数f(x)=x2+(k-4)x-2k+4的值恒大于零,则x的取值范围是
A.x<0 B.x>4 C.x<1或x>3 D.x<1
2.已知f(x)=1-(x-a)(x-b),并且m,n是方程f(x)=0的两根,则实数a,b,m,n的大小关系可能是( )
A. m<a<b<n B.a<m<n<b C.a<m<b<n D.m<a<n<b
1.如果抛物线f(x)= x2+bx+c的图象与x轴交于两点(-1,0)和(3,0),则f(x)>0的解集是( )
A. (-1,3) B.[-1,3] C.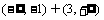 D.
D. 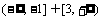
20.已知: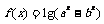 (a>1>b>0).
(a>1>b>0).
(1)求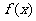 的定义域;(2)判断
的定义域;(2)判断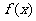 在其定义域内的单调性;
在其定义域内的单调性;
(3)若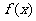 在(1,+∞)内恒为正,试比较a-b与1的大小.
在(1,+∞)内恒为正,试比较a-b与1的大小.
 必修1
第2章 函数概念与基本初等函数Ⅰ
必修1
第2章 函数概念与基本初等函数Ⅰ
§2.5函数与方程
重难点:理解根据二次函数的图象与x轴的交点的个数判断一元二次方程的根的个数及函数零点的概念,对“在函数的零点两侧函数值乘积小于0”的理解;通过用“二分法”求方程的近似解,使学生体会函数的零点与方程根之间的关系,初步形成用函数观点处理问题的意识.
考纲要求:①结合二次函数的图像,了解函数的零点与方程根的联系,判断一元二次方程根的存在性及根的个数;
②根据具体函数的图像,能够用二分法求相应方程的近似解.
经典例题:研究方程|x2-2x-3|=a(a≥0)的不同实根的个数.
当堂练习:
19. 已知f (x)=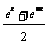 且x∈[0, +∞ )
且x∈[0, +∞ )
(1) 判断f (x)的奇偶性; (2) 判断f (x)的单调性,并用定义证明;(3) 求y=f (x)的反函数的解析式.
18.已知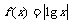 ,若当
,若当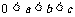 时,
时, ,试证:
,试证: 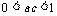
17.已知f (x)=lg(x2+1), 求满足f (100x-10x+1)-f (24)=0的x的值
16.化简与求值: (1)已知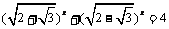 ,求x的值;
,求x的值;
(2)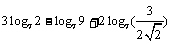 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com