
3、我国是手机生产大国,可是拥有自主知识产权的手机企业并不多。一些企业“只顾贴牌,不顾创新”,在别人知识产权包围下的危机业已显现。这启示我们
A.要坚持以经济建设为中心,一心一意谋发展
B.要深化改革,调整生产关系中与生产力不相适应的部分
C.必须大力推进科技进步和自主创新
D.要积极发展对外经济技术交流与合作
2、国务院常务会议决定,加快推进电信网、广播电视网和互联网三网融合。网络新业务与新体验不断涌现,使得公众对多业务的综合需求日益强烈。这说明
A.生产决定消费 B.消费对生产具有反作用
C.消费决定生产 D.消费是生产的目的和动力
1、小黄在网上购得《2012》电影票,去电影院观赏了影视作品,从经济活动的角度看,小黄的行为属于
A.生产活动与交换活动 B.交换活动与分配活动
C.分配活动与消费活动 D.交换活动与消费活动
22.(本小题满分14分)
正实数数列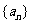 中,
中,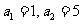 ,且
,且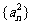 成等差数列.
成等差数列.
(1) 证明数列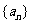 中有无穷多项为无理数;
中有无穷多项为无理数;
(2)当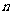 为何值时,
为何值时,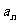 为整数,并求出使
为整数,并求出使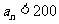 的所有整数项的和.
的所有整数项的和.
[解析]考查等差数列及数列分组求和知识
证明:(1)由已知有: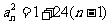 ,从而
,从而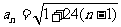 ,
,
方法一:取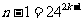 ,则
,则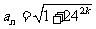 (
(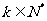 )
)
用反证法证明这些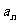 都是无理数.
都是无理数.
假设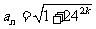 为有理数,则
为有理数,则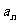 必为正整数,且
必为正整数,且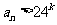 ,
,
故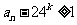 .
.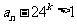 ,与
,与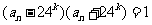 矛盾,
矛盾,
所以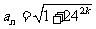 (
(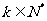 )都是无理数,即数列
)都是无理数,即数列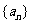 中有无穷多项为无理数;
中有无穷多项为无理数;
方法二:因为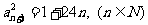 ,当
,当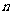 的末位数字是
的末位数字是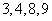 时,
时,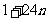 的末位数字是
的末位数字是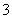 和
和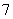 ,它不是整数的平方,也不是既约分数的平方,故此时
,它不是整数的平方,也不是既约分数的平方,故此时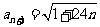 不是有理数,因这种
不是有理数,因这种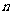 有无穷多,故这种无理项
有无穷多,故这种无理项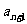 也有无穷多.
也有无穷多.
(2) 要使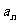 为整数,由
为整数,由 可知:
可知:
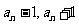 同为偶数,且其中一个必为3的倍数,所以有
同为偶数,且其中一个必为3的倍数,所以有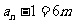 或
或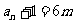
当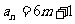 时,有
时,有 (
(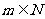 )
)
又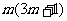 必为偶数,所以
必为偶数,所以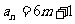 (
(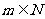 )满足
)满足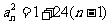
即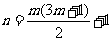 (
(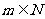 )时,
)时,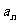 为整数;
为整数;
同理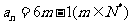 有
有 (
(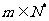 )
)
也满足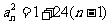 ,即
,即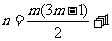 (
(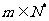 )时,
)时,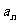 为整数;
为整数;
显然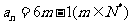 和
和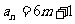 (
(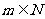 )是数列中的不同项;
)是数列中的不同项;
所以当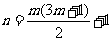 (
(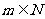 )和
)和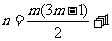 (
(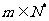 )时,
)时,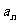 为整数;
为整数;
由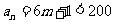 (
(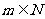 )有
)有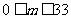 ,
,
由 (
(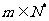 )有
)有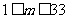 .
.
设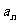 中满足
中满足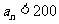 的所有整数项的和为
的所有整数项的和为 ,则
,则

绝密★启用前 秘密★启用后
2010年普通高等学校招生全国统一考试(江西卷)
21.(本小题满分12分)
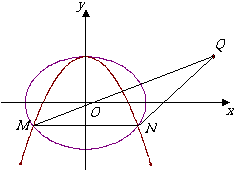 已知抛物线
已知抛物线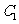 :
: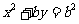 经过椭圆
经过椭圆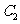 :
: 的两个焦点.
的两个焦点.
(1) 求椭圆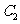 的离心率;
的离心率;
(2) 设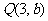 ,又
,又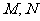 为
为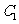 与
与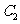 不在
不在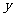 轴上的两个交点,若
轴上的两个交点,若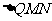 的重心在抛物线
的重心在抛物线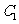 上,求
上,求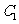 和
和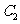 的方程.
的方程.
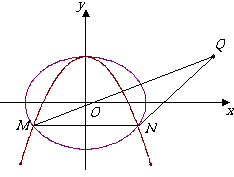 [解析]考查椭圆和抛物线的定义、基本量,通过交点三角形来确认方程。
[解析]考查椭圆和抛物线的定义、基本量,通过交点三角形来确认方程。
解:(1)因为抛物线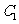 经过椭圆
经过椭圆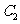 的两个焦点
的两个焦点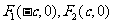 ,
,
所以 ,即
,即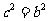 ,由
,由 得椭圆
得椭圆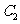 的离心率
的离心率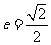 .
.
(2)由(1)可知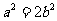 ,椭圆
,椭圆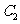 的方程为:
的方程为:
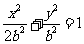
联立抛物线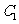 的方程
的方程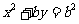 得:
得: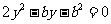 ,
,
解得: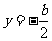 或
或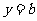 (舍去),所以
(舍去),所以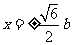 ,
,
即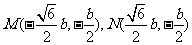 ,所以
,所以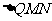 的重心坐标为
的重心坐标为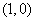 .
.
因为重心在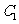 上,所以
上,所以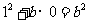 ,得
,得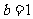 .所以
.所以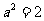 .
.
所以抛物线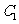 的方程为:
的方程为: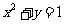 ,
,
椭圆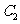 的方程为:
的方程为: .
.
20.(本小题满分12分)
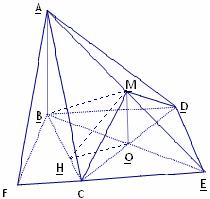
 如图,
如图,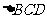 与
与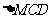 都是边长为2的正三角形,平面
都是边长为2的正三角形,平面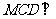 平面
平面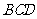 ,
,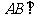 平面
平面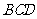 ,
,
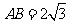 .
.
(1)求直线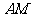 与平面
与平面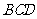 所成的角的大小;
所成的角的大小;
(2)求平面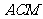 与平面
与平面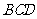 所成的二面角的正弦值.
所成的二面角的正弦值.
 [解析]本题主要考查了考查立体图形的空间感、线面角、二面角、空间向量、二面角平面角的判断有关知识,同时也考查了空间想象能力和推理能力
[解析]本题主要考查了考查立体图形的空间感、线面角、二面角、空间向量、二面角平面角的判断有关知识,同时也考查了空间想象能力和推理能力
解法一:(1)取CD中点O,连OB,OM,则OB⊥CD,OM⊥CD.
又平面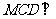 平面
平面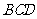 ,则MO⊥平面
,则MO⊥平面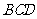 ,所以MO∥AB,A、B、O、M共面.延长AM、BO相交于E,则∠AEB就是AM与平面BCD所成的角.
,所以MO∥AB,A、B、O、M共面.延长AM、BO相交于E,则∠AEB就是AM与平面BCD所成的角.
 OB=MO=
OB=MO=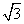 ,MO∥AB,则
,MO∥AB,则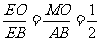 ,
,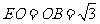 ,所以
,所以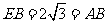 ,故
,故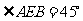 .
.
(2)CE是平面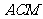 与平面
与平面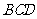 的交线.
的交线.
由(1)知,O是BE的中点,则BCED是菱形.
作BF⊥EC于F,连AF,则AF⊥EC,∠AFB就是二面角A-EC-B的平面角,设为 .
.
因为∠BCE=120°,所以∠BCF=60°.
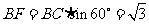 ,
,
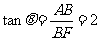 ,
,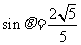
所以,所求二面角的正弦值是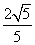 .
.
 解法二:取CD中点O,连OB,OM,则OB⊥CD,OM⊥CD,又平面
解法二:取CD中点O,连OB,OM,则OB⊥CD,OM⊥CD,又平面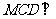 平面
平面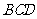 ,则MO⊥平面
,则MO⊥平面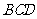 .
.
以O为原点,直线OC、BO、OM为x轴,y轴,z轴,建立空间直角坐标系如图.
OB=OM=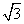 ,则各点坐标分别为O(0,0,0),C(1,0,0),M(0,0,
,则各点坐标分别为O(0,0,0),C(1,0,0),M(0,0,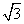 ),B(0,-
),B(0,-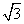 ,0),A(0,-
,0),A(0,-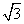 ,2
,2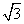 ),
),
(1)设直线AM与平面BCD所成的角为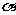 .
.
因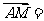 (0,
(0,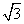 ,
,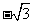 ),平面
),平面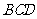 的法向量为
的法向量为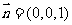 .则有
.则有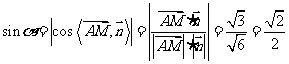 ,所以
,所以 .
.
(2)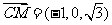 ,
,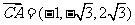 .
.
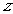 设平面ACM的法向量为
设平面ACM的法向量为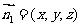 ,由
,由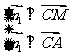 得
得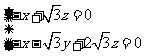 .解得
.解得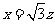 ,
,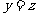 ,取
,取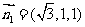 .又平面BCD的法向量为
.又平面BCD的法向量为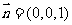 ,则
,则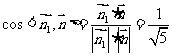
设所求二面角为 ,则
,则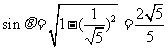 .
.
19.(本小题满分12分)
已知函数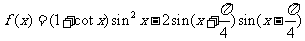 .
.
(1)若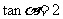 ,求
,求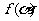 ;
;
(2)若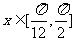 ,求
,求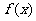 的取值范围.
的取值范围.
[解析]考查三角函数的化简、三角函数的图像和性质、三角函数值域问题。依托三角函数化简,考查函数值域,作为基本的知识交汇问题,考查基本三角函数变换,属于中等题.
解:(1)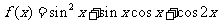
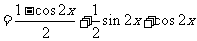
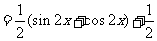
由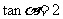 得
得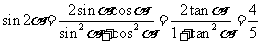 ,
,
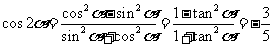 ,
,
所以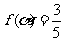 .
.
(2)由(1)得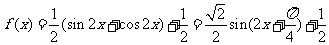
由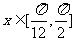 得
得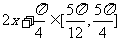 ,所以
,所以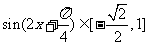
从而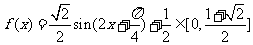 .
.
18.(本小题满分12分)
某迷宫有三个通道,进入迷宫的每个人都要经过一扇智能门。首次到达此门,系统会随机(即等可能)为你打开一个通道.若是1号通道,则需要1小时走出迷宫;若是2号、3号通道,则分别需要2小时、3小时返回智能门.再次到达智能门时,系统会随机打开一个你未到过的通道,直至走出迷宫为止.
(1)求走出迷宫时恰好用了1小时的概率;
(2)求走出迷宫的时间超过3小时的概率.
[解析]考查数学知识的实际背景,重点考查相互独立事件的概率乘法公式计算事件的概率、随机事件的数学特征和对思维能力、运算能力、实践能力的考查。
解:(1)设A表示走出迷宫时恰好用了1小时这一事件,则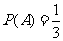 .
.
(2) 设B表示走出迷宫的时间超过3小时这一事件,则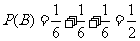 .
.
17.(本小题满分12分)
设函数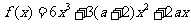 .
.
(1)若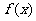 的两个极值点为
的两个极值点为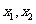 ,且
,且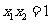 ,求实数
,求实数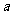 的值;
的值;
(2)是否存在实数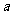 ,使得
,使得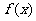 是
是 上的单调函数?若存在,求出
上的单调函数?若存在,求出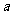 的值;若不存在,说明理由.
的值;若不存在,说明理由.
[解析]考查函数利用导数处理函数极值单调性等知识
解: 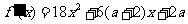
(1)由已知有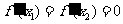 ,从而
,从而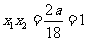 ,所以
,所以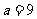 ;
;
(2)由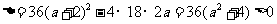 ,
,
所以不存在实数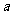 ,使得
,使得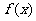 是
是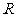 上的单调函数.
上的单调函数.
16.长方体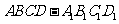 的顶点均在同一个球面上,
的顶点均在同一个球面上,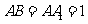 ,
,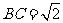 ,则
,则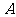 ,
,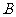 两点间的球面距离为
.
两点间的球面距离为
.
[答案]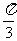
[解析]考查球面距离,可先利用长方体三边长求出球半径,在三角形中求出球心角,再利用球面距离公式得出答案
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com