
7.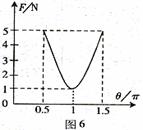 在研究两个共点力合成的实验中得到如图6所示的合力F与两个分力的夹角的关系图。问:(1)两个分力的大小各是多少?(2)合力的变化范围是多少?
在研究两个共点力合成的实验中得到如图6所示的合力F与两个分力的夹角的关系图。问:(1)两个分力的大小各是多少?(2)合力的变化范围是多少?
解析:(1)由图6得,当或时,合力F为5N,即
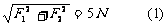
当时,合力为1N,即: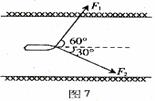
由(1)、(2)解得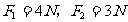
(2)合力的变化范围是
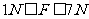
6、在例2中,如果保持A、O位置不变,当B点逐渐向上移动到O点的正上方时,AO、BO绳的拉力大小是如何变化的?
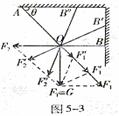 解析:由上题分析得,OC绳的拉力效果有两个,一是沿AO绳拉紧AO的效果,另一个是沿BO绳使BO绳拉紧的效果。根据OC绳拉力的效果,用平行四边形定则,作出OC绳的拉力和两个分力在OB绳方向变化时的几个平行四边形,如图5-3所示。由图可知,当B点位置逐渐变化到B’、B’’的过程中,表示大小的线段的长度在逐渐减小。故在不断减小;表示大小的线段
解析:由上题分析得,OC绳的拉力效果有两个,一是沿AO绳拉紧AO的效果,另一个是沿BO绳使BO绳拉紧的效果。根据OC绳拉力的效果,用平行四边形定则,作出OC绳的拉力和两个分力在OB绳方向变化时的几个平行四边形,如图5-3所示。由图可知,当B点位置逐渐变化到B’、B’’的过程中,表示大小的线段的长度在逐渐减小。故在不断减小;表示大小的线段 的长度先减小后增大,故是先减小后增大。
的长度先减小后增大,故是先减小后增大。
说明:在分析分力如何变化时,一般采用图解法来分析比较容易和方便。
5.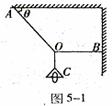 如图5-1所示,电灯的重力为,AO绳与顶板间的夹角为,BO绳水平,则AO绳所受的拉力和BO绳所受的拉力分别为多少?
如图5-1所示,电灯的重力为,AO绳与顶板间的夹角为,BO绳水平,则AO绳所受的拉力和BO绳所受的拉力分别为多少?
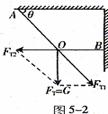 解析;先分析物理现象,为什么绳AO、BO受到拉力呢?原因是OC绳受到电灯的拉力使绳张紧产生的,因此OC绳的拉力产生了两个效果,一是沿AO向下的拉竖AO的分力,另一个是沿BO绳向左的拉紧BO绳的分力。画出平行四边形,如图5-2所示。因为OC绳的拉力等于电灯的重力,因此由几何关系得
解析;先分析物理现象,为什么绳AO、BO受到拉力呢?原因是OC绳受到电灯的拉力使绳张紧产生的,因此OC绳的拉力产生了两个效果,一是沿AO向下的拉竖AO的分力,另一个是沿BO绳向左的拉紧BO绳的分力。画出平行四边形,如图5-2所示。因为OC绳的拉力等于电灯的重力,因此由几何关系得
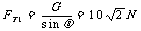
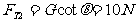
其方向分别为沿AO方向和沿BO方向(如图5-2所示)。
4、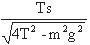 两根长度相等的轻绳,下端悬挂一质量为m的物体,上端分别固定在水平天花板上的M、N点,M、N两点间的距离为s,如图所示。已知两绳所能经受的最大拉力均为T,则每根绳的长度不得短于_______。
两根长度相等的轻绳,下端悬挂一质量为m的物体,上端分别固定在水平天花板上的M、N点,M、N两点间的距离为s,如图所示。已知两绳所能经受的最大拉力均为T,则每根绳的长度不得短于_______。
3. 如图所示,固定在水平面上的光滑半球,球心O的正上方固定一个小定滑轮,细绳一端拴一小球,小球置于半球面上的A点,另一端绕过定滑轮.今缓慢拉绳使小球从A点滑到半球顶点,则此过程中,小球对半球的压力N及细绳的拉力F大小变化情况是(C)
如图所示,固定在水平面上的光滑半球,球心O的正上方固定一个小定滑轮,细绳一端拴一小球,小球置于半球面上的A点,另一端绕过定滑轮.今缓慢拉绳使小球从A点滑到半球顶点,则此过程中,小球对半球的压力N及细绳的拉力F大小变化情况是(C)
A.N变大,F变大 B. N变小,F变大
C.N不变,F变小 D. N变大,F变小
2.如图所示,A、B两物体的质量分别为mA和mB,且mA>mB,整个系统处于静止状态,滑轮的质量和一切摩擦均不计.如果绳一端由Q点缓慢地向左移到P点,整个系统
 重新平衡后,物体A的高度和两滑轮间绳与水平方向的夹角θ如何变化?(C)
重新平衡后,物体A的高度和两滑轮间绳与水平方向的夹角θ如何变化?(C)
A.物体A的高度升高,θ角变大 B.物体A的高度降低,θ角变小
C.物体A的高度升高,θ角不变 D.物体A的高度不变,θ角变小
1. 如图所示,用一根长为L的细绳一端固定在O点,另一端悬挂质量为m的小球A,为使细绳与竖直方向夹300角且绷紧,小球A处于静止,则需对小球施加的最小力等于( C )
如图所示,用一根长为L的细绳一端固定在O点,另一端悬挂质量为m的小球A,为使细绳与竖直方向夹300角且绷紧,小球A处于静止,则需对小球施加的最小力等于( C )
A.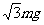 B.
B.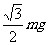 C.
C.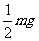 D.
D.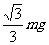
4.力的分解
 求一个已知力的分力叫力的分解.力的分解是力的合成的逆运算,也遵从平行四边形定则.一个已知力可以分解为无数对大小和方向不同的分力,在力的分解过程中,常常要考虑到力实际产生的效果,这样才能使力的分解具有唯一性.要使分力有唯一解,必须满足:已知两个分力的方向或已知一个分力的大小和方向.
求一个已知力的分力叫力的分解.力的分解是力的合成的逆运算,也遵从平行四边形定则.一个已知力可以分解为无数对大小和方向不同的分力,在力的分解过程中,常常要考虑到力实际产生的效果,这样才能使力的分解具有唯一性.要使分力有唯一解,必须满足:已知两个分力的方向或已知一个分力的大小和方向.
注意:已知一个分力(F2)大小和另一个分力(F1)的方向
(F1与F2的夹角为θ),则有三种可能:
①F2<Fsinθ时无解
②F2=Fsinθ或F2≥F时有一组解
③Fsinθ< F2<F时有两组解
5 解题的方法
求合力的方法
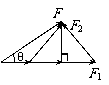
(1)作图法。作图法是先作力的图示,然后根据平行四边形定则作如图1所示的平行四边形,或如图2、3所示的三角形,再根据相同的标度,确定出合力的大小,再用量角器量出角度的大小,即合力的方向。
(2)公式法。公式法是根据合力和分力的大小关系,用公式
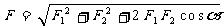
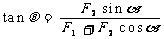
或用正弦定理、相似三角形的规律等数学知识来求合力大小和方向的方法。
(3)正交分解法。正交分解法就是把力沿着两个选定的互相垂直的方向上先分解,后合成的方法。其目的是便于运用普通代数运算公式来解决适量的运算,它是处理合成和分解复杂问题的一种简便方法。
求分力的方法
(1)分解法。一般按力对物体实际作用的效果进行分解的方法。
 (2)图解法。根据平行四边形定则,作出合力与分力所构成的首尾相接的矢量三角形,利用边、角间的关系分析力的大小变化情况的方法。
(2)图解法。根据平行四边形定则,作出合力与分力所构成的首尾相接的矢量三角形,利用边、角间的关系分析力的大小变化情况的方法。
[典型例题]
例1.4N、7N、9N三个共点力,最大合力为 20N ,最小合力是 0N .
例2.轻绳AB总长l,用轻滑轮悬挂重G的物体。绳能承受的最大拉力是2G,将A端固定,将B端缓慢向右移动d而使绳不断,求d的最大可能值.
 解:以与滑轮接触的那一小段绳子为研究对象,在任何一个平衡位置都在滑轮对它的压力(大小为G)和绳的拉力F1、F2共同作用下静止。而同一根绳子上的拉力大小F1、F2总是相等的,它们的合力N是压力G的平衡力,方向竖直向上。因此以F1、F2为分力做力的合成的平行四边形一定是菱形。利用菱形对角线互相垂直平分的性质,结合相似形知识可得:
解:以与滑轮接触的那一小段绳子为研究对象,在任何一个平衡位置都在滑轮对它的压力(大小为G)和绳的拉力F1、F2共同作用下静止。而同一根绳子上的拉力大小F1、F2总是相等的,它们的合力N是压力G的平衡力,方向竖直向上。因此以F1、F2为分力做力的合成的平行四边形一定是菱形。利用菱形对角线互相垂直平分的性质,结合相似形知识可得:
d∶l =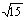 ∶4,所以d最大为
∶4,所以d最大为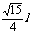

 例3.将一个大小为F的力分解为两个分力,其中一个分力F1的方向跟F成600角,当另一个分力F2有最小值时,F1的大小为
例3.将一个大小为F的力分解为两个分力,其中一个分力F1的方向跟F成600角,当另一个分力F2有最小值时,F1的大小为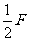 ,F2的大小为
,F2的大小为 .
.
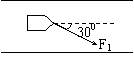
例4.如图所示,河道内有一艘小船,有人用100N的力F1与
河道成300拉船.现要使船始终沿河道前进,则至少需加多大的力才
行?这个力的方向如何?(50N,方向与河岸垂直)
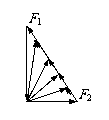 例5.重G的光滑小球静止在固定斜面和竖直挡板之间。若挡板逆时针缓慢转到水平位置,在该过程中,斜面和挡板对小球的弹力的大小F1、F2各如何变化?
例5.重G的光滑小球静止在固定斜面和竖直挡板之间。若挡板逆时针缓慢转到水平位置,在该过程中,斜面和挡板对小球的弹力的大小F1、F2各如何变化?
解:由于挡板是缓慢转动的,可以认为每个时刻小球都处于静止状态,因此所受合力为零。应用三角形定则,G、F1、F2三个矢量应组成封闭三角形,其中G的大小、方向始终保持不变;F1的方向不变;F2的起点在G的终点处,而终点必须在F1所在的直线上,由作图可知,挡板逆时针转动90°过程,F2矢量也逆时针转动90°,因此F1逐渐变小,F2先变小后变大.(当F2⊥F1,即挡板与斜面垂直时,F2最小)
[针对训练]
3.根据力的平行四边形定则可得出以下几个结论:
①共点的两个力(F1、F2)的合力(F)的大小,与它们的夹角(θ)有关;θ越大,合力越小;θ越小,合力越大.F1与F2同向时合力最大;F1与F2反向时合力最小,合力的取值范围是:│F1-F2│≤F≤F1+F2
②合力可能比分力大,也可能比分力小,也可能等于某一分力.
③共点的三个力,如果任意两个力的合力最小值小于或等于第三个力,那么这三个共点力的合力可能等于零.
2.力的平行四边形定则
求两个互成角度的力的合力,可以用表示这两个力的线段为邻边作平行四边形,它的对角线就表示合力的大小和方向.
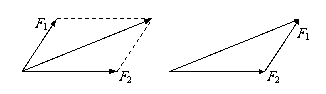 说明:①矢量的合成与分解都遵从平行四边形定则(可简化成三角形定则)
说明:①矢量的合成与分解都遵从平行四边形定则(可简化成三角形定则)
②力的合成和分解实际上是一种等效替代.
③由三角形定则还可以得到一个有用的推论:如果n个力首尾相接组成一个封闭多边形,则这n个力的合力为零.
④在分析同一个问题时,合矢量和分矢量不能同时使用.也就是说,在分析问题时,考虑了合矢量就不能再考虑分矢量;考虑了分矢量就不能再考虑合矢量.
⑤矢量的合成分解,一定要认真作图.在用平行四边形定则时,分矢量和合矢量要画成带箭头的实线,平行四边形的另外两个边必须画成虚线.各个矢量的大小和方向一定要画得合理.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com