1．“人类之得以为人，不至永沦奴籍者，非法兰西人之赐而谁耶？”这是陈独秀对下列哪一文选的称赞　　　　　 　　　　　　　　　 (　　 )

　　 A．《权利法案》　　 B．《人权宣言》　 C．《独立宣言》 　　 D．《大宪章》

2.某蔬菜基地种植西红柿，由历年市场行情得知，从二月一日起的300天内，西红柿市场售价与上市时间的关系用图2-10中(1)的一条折线表示；西红柿的种植成本与上市时间的关系用图2-10中(2)的抛物线表示.

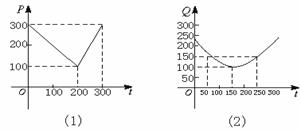
图2-10

(1)写出图中(1)表示的市场售价与时间的函数关系式P＝f(t)；

写出图中(2)表示的种植成本与时间的函数关系式Q＝g(t)；

(2)认定市场售价减去种植成本为纯收益，问何时上市的西红柿纯收益最大?

[学后反思]____________________________________________________ _______

　　　　　 _____________________________________________________________

　　　　　 _____________________________________________________________

1. 围建一个面积为360m²的矩形场地，要求矩形场地的一面利用旧墙(利用旧墙需维修)，其它三面围墙要新建，在旧墙的对面的新墙上要留一个宽度为2m的进出口，如图所示，已知旧墙的维修费用为45元/m,新墙的造价为180元/m,设利用的旧墙的长度为x，总费用为y (单位：元)。。

(Ⅰ)将y表示为x的函数;w.w.w.k.s.

　　 　(Ⅱ)试确定x,使修建此矩形场地围墙的总费用最小，

并求出最小总费用。

3．求解函数模型：根据实际问题所需要解决的目标及函数式的结构特点正确选择函数知识求得函数模型的解，并还原为实际问题的解.

这些步骤用框图表示是：

这些步骤用框图表示：

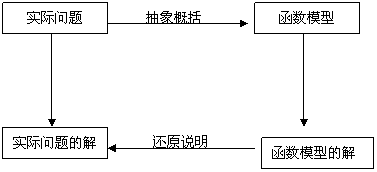
[典型例析]

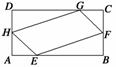
例1. 如图所示，在矩形ABCD中，已知AB=a，BC=b(b＜a),在AB，AD，CD，CB上分别截取AE，AH，CG，CF都等于x，当x为何值时，四边形EFGH的面积最大？并求出最大面积.

变式训练1：某商人将进货单价为8元的某种商品按10元一个销售时，每天可卖出100个，现在他采用提高售价，减少进货量的办法增加利润，已知这种商品销售单价每涨1元，销售量就减少10个，问他将售价每个定为多少元时，才能使每天所赚的利润最大？并求出最大值.

例2. 据气象中心观察和预测：发生于M地的沙尘暴一直向正南方向移动，其移动速度

v(km/h)与时间t(h)的函数图象如图所示，过线段OC上一点T(t，0)作横轴

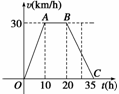的垂线l，梯形OABC在直线l左侧部分的面积即为t(h)内沙尘暴所经过的路程s(km).(1)当t=4时，求s的值；

(2)将s随t变化的规律用数学关系式表示出来；

(3)若N城位于M地正南方向，且距M地650 km，试判断这

场沙尘暴是否会侵袭到N城，如果会，在沙尘暴发生后多长时间它将

侵袭到N城？如果不会，请说明理由.

变式训练2：某工厂生产一种机器的固定成本(即固定投入)为0.5万元，但每生产100台，

需要加可变成本(即另增加投入)0.25万元.市场对此产品的年需求量为500台，销售的收入函数为R(x)=5x-(万元)(0≤x≤5)，其中x是产品售出的数量(单位：百台).

(1)把利润表示为年产量的函数；

(2)年产量是多少时，工厂所得利润最大？

(3)年产量是多少时，工厂才不亏本？

例3. 某市居民自来水收费标准如下：每户每月用水不超过4吨时，每吨为1.80元，当用水超过4吨时，超过部分每吨3.00元，某月甲、乙两户共交水费y元，已知甲、乙两用户该月用水量分别为5x，3x吨.

(1)求y关于x的函数；

(2)若甲、乙两户该月共交水费26.4元，分别求出甲、乙两户该月的用水量和水费.

[当堂检测]

2．建立函数模型：将变量y表示为x的函数，在中学数学内，我们建立的函数模型一般都是函数的解析式；

1．抽象概括：研究实际问题中量，确定变量之间的主、被动关系，并用x、y分别表示问题中的变量；

2.培养综合解决问题能力

4以极度的热情投入学习，体会成功的快乐。

[学习重点]

函数与方程的相互转化

[学习难点]

函数与方程的相互转化

　[自主学习]

1．能根据题目条件建立正确的函数模型并能利用函数性质解决问题

28．自20世纪90年代以来，稠环化合物的研究开发工作十分迅速，这一类物质在高科技领域有着十分广泛的应用前景。下面是苯和一系列稠环芳香烃的结构简式：

试解答下列问题：

(1)写出化合物②⑤的分子式：

①C₆H₆　 ②_____________ ③____________ ④____________ ⑤

(2)这组化合物分子式的通式是：

(3)某课外兴趣小组，做了系列实验，他们将该系列的前5种芳香烃逐一加到浓的酸性高锰酸钾溶液中加热。结果发现，只有苯无明显变化，其余4种物质都能使酸性高锰钾溶

液褪色。经分析知后4种稠环芳烃的氧化产物是：、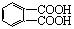

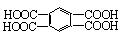
或者两者都有。由此你能得出的结论是：__________________，

(4)甲、乙、丙三同学同做酸性高锰酸钾溶液氧化并五苯的实验。甲将氧化后的混合液酸化分离得到一种无色晶体X，称取0.2540g X，用热水配成100mL溶液中和滴定，取出25.00mL，用0.1000mol·L^-1 NaOH溶液中和滴定，滴到10.00mL时达到终点；丙用酸性高锰酸钾氧化并五苯，将氧化后的混合液酸化分离得到无色晶体Y，中和测定知Y的中和能力只有X的中和能力的一半；乙用酸性高锰钾溶液氧化并五苯，将氧化后的混合液酸化分离得无色晶体，经分析其中包含了甲与丙得的两种成份，通过计算推理确定X的结构简式。

(5)在Y的同分异构体中与Y同属芳香族化合物既可看作羧酸类，又可看作酯类的同分异构体的结构简式有：______________________________________________________ ，

在Y的同分异构体中既不属于羧酸类，又不属于酯类，但可看作常见芳香烃的衍生物的同分异构体的结构简式有(写一种)

27．为探究乙炔与溴的加成反应，甲同学设计并进行了如下实验：先取一定量工业用电石与水反应，将生成的气体通入溴水中，发现溶液褪色，即证明乙炔与溴水发生了加成反应。乙同学发现在甲同学的实验中，褪色后的溶液里有少许淡黄色的浑浊，推测在制得的乙炔中还可能含有少量还原性的杂质气体，由此他提出必须除去之，再与溴水反应。

请你回答下列问题：

(1)甲同学设计的实验_______(填“能”或“不能”)验证乙炔与溴发生加成反应，其理由是_______。

a.使溴水褪色的反应，未必是加成反应

b.使溴水褪色的反应，就是加成反应

c.使溴水褪色的物质，未必是乙炔

d.使溴水褪色的物质，就是乙炔

(2)乙同学推测此乙炔中必定含有一种杂质气体是_______，它与溴水反应的化学方程式是_______；在验证过程中必须全部除去。

(3)请你选用图2-2所列四个装置(可重复使用)试验乙同学的实验方案，将它们的编号填入方框，并在括号中写出装置内所放的化学药品。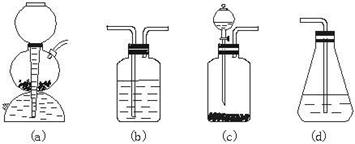

图2-2

(4)为验证这一反应是加成而不是取代反应，丙同学提出可用pH试纸来测试反应后溶液的酸性，理由是_______。