
21、(12分)已知函数 定义在区间
定义在区间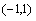 上,
上,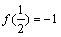 ,且当
,且当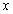 、
、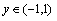 时,恒有
时,恒有
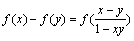 。又数列
。又数列 满足
满足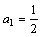 ,
,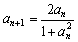 。
。
设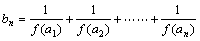 。
。
⑴
证明: 在
在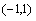 上为奇函数;
上为奇函数;
⑵
求 的表达式;
的表达式;
⑶
是否存在正整数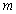 ,使得对任意
,使得对任意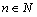 ,都有
,都有 成立,若存在,求出
成立,若存在,求出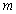 的最小值;若不存在,请说明理由。
的最小值;若不存在,请说明理由。
20、(12分)某工厂有216名工人接受了生产1000台GH型高科技产品的总任务。已知每台GH型产品由4个G型装置和3个H型装置配套组成,每个工人每小时能加工6个G型装置或3个H型装置。现将工人分成两组同时开始加工,每组分别加工一种装置。设加工G型装置的工人有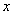 人,他们加工完G型装置所需时间为
人,他们加工完G型装置所需时间为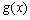 ,其余工人加工完H型装置所需时间为
,其余工人加工完H型装置所需时间为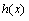 (单位:小时,可以不是整数)。
(单位:小时,可以不是整数)。
⑴ 写出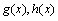 解析式;
解析式;
⑵ 比较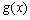 与
与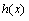 的大小,并写出这216名工人完成总任务的时间
的大小,并写出这216名工人完成总任务的时间 的解析式;
的解析式;
⑶ 应怎样分组,才能使完成总任务用的时间最少?
19、(12分)已知函数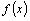 定义域是
定义域是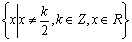 ,且
,且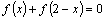 ,
,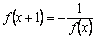 ,
,
当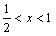 时:
时: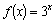 。
。
⑴
判断 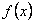 奇偶性,并证明;
奇偶性,并证明;
⑵ 求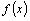 在
在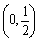 上的表达式;
上的表达式;
⑶ 是否存在正整数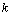 ,使得
,使得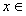
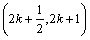 时,
时,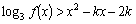 有解,并说明理由。
有解,并说明理由。
18、(12分)设函数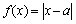 ,
,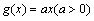 。
。
⑴
解关于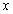 的不等式
的不等式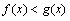 ;
;
⑵
设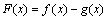 ,若
,若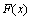 在
在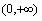 上有最小值,求
上有最小值,求 的取值范围。
的取值范围。
17、(12分)设命题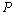 :函数
:函数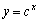 在
在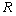 上单调递减;命题
上单调递减;命题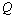 :不等式
:不等式 的解集为
的解集为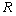 。若
。若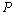
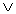
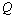 为真,
为真,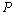
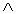
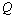 为假,求实数
为假,求实数 的取值范围。
的取值范围。
16、若不等式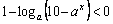 有解,则实数
有解,则实数 的取值范围是
。
的取值范围是
。
15、已知 ,
,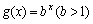 ,当
,当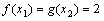 时,有
时,有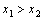 ,则
,则 、
、 的大小关系是
。
的大小关系是
。
14、已知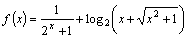 ,则
,则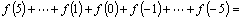 。
。
13、若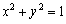 ,则
,则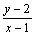 的最小值是___
_______。
的最小值是___
_______。
12、已知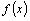 是定义在实数集R上的不恒为零的函数,且对于任意
是定义在实数集R上的不恒为零的函数,且对于任意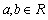 ,满足
,满足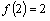 ,
,
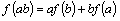 ,记
,记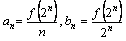 ,其中n∈N*。考查下列结论:①
,其中n∈N*。考查下列结论:①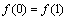
②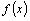 是
是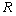 上的偶函数 ③ 数列
上的偶函数 ③ 数列 为等比数列 ④ 数列
为等比数列 ④ 数列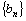 为等差数列,其中不正确的是
为等差数列,其中不正确的是
A.① B.② C.③ D.④
第Ⅱ卷(非选择题 共90分)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com