
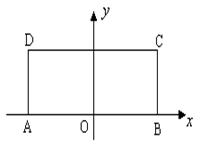
12、 已知长方形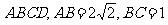 ,以
,以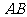 的中点
的中点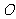 为原点建立如图所示的平面直角坐标系
为原点建立如图所示的平面直角坐标系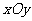 .
.
(Ⅰ)求以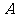 、
、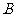 为焦点,且过
为焦点,且过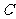 、
、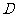 两点的椭圆的标准方程;
两点的椭圆的标准方程;
 。(Ⅱ)过点
。(Ⅱ)过点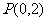 的直线
的直线 交(Ⅰ)中椭圆于
交(Ⅰ)中椭圆于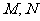 两点, 判断是否存在直线
两点, 判断是否存在直线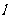 ,使得以弦
,使得以弦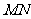 为直径的圆恰好过原点,并说明理由.
为直径的圆恰好过原点,并说明理由.
解:(Ⅰ)由题意可得点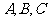 的坐标分别为
的坐标分别为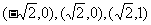 .……2分
.……2分
设椭圆的标准方程为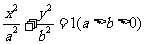 ,则有
,则有
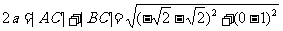 +
+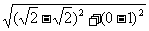
=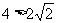 ,
,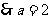 ,
,
椭圆的标准方程为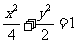 .
……9分
.
……9分
(Ⅱ)假设满足条件的直线 存在,由条件可知直线
存在,由条件可知直线 的斜率存在,
的斜率存在,
设直线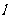 的方程为:
的方程为: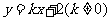 ;设
;设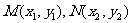 .
.
联立方程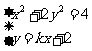 ,消去
,消去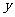 并整理得
并整理得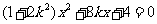
有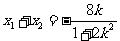 ,
, ……12分
……12分
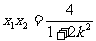
有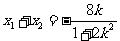 ,
, ……12分
……12分
若以弦 为直径的圆恰好过原点,则
为直径的圆恰好过原点,则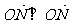 ,所以
,所以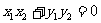
即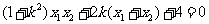 ,所以
,所以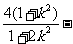
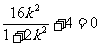
即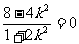 ,解得
,解得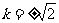 ……14分
……14分
验知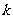 值满足判别式
值满足判别式
所以,直线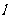 的方程为
的方程为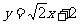 或
或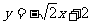 .
……16分
.
……16分
11.(本小题满分14分)
已知关于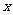 的一元二次函数
的一元二次函数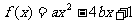 .
.
(1)设集合P={1,2,
3}和Q={-1,1,2,3,4},分别从集合P和Q中随机取一个数作为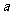 和
和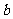 ,求函数
,求函数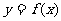 在区间[
在区间[ 上是增函数的概率;
上是增函数的概率;
(2)设点(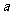 ,
,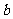 )是区域
)是区域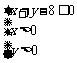 内的随机点,求
内的随机点,求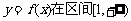 上是增函数的概率.
上是增函数的概率.
解:(1)∵函数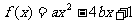 的图象的对称轴为
的图象的对称轴为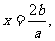
要使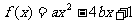 在区间
在区间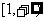 上为增函数,
上为增函数,
当且仅当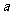 >0且
>0且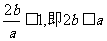 ……………………………3分
……………………………3分
若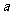 =1则
=1则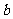 =-1, 若
=-1, 若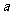 =2则
=2则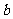 =-1,1; 若
=-1,1; 若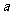 =3则
=3则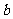 =-1,1; …………5分
=-1,1; …………5分
∴事件包含基本事件的个数是1+2+2=5
∴所求事件的概率为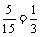 . ……………………………7分
. ……………………………7分
(2)由(Ⅰ)知当且仅当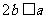 且
且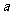 >0时,
>0时,
函数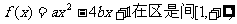 上为增函数,
上为增函数,
依条件可知试验的全部结果所构成的区域为
构成所求事件的区域为三角形部分. 由 …11分
…11分
∴所求事件的概率为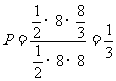 . ………………………… 14分
. ………………………… 14分
10、 曲边梯形由曲线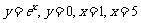 所围成,过曲线
所围成,过曲线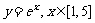 上一点P作切线,使得此切线从曲边梯形上切出一个面积最大的普通梯形,这时点P的坐标是 ▲ . .
上一点P作切线,使得此切线从曲边梯形上切出一个面积最大的普通梯形,这时点P的坐标是 ▲ . .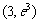
二解答题
9、已知P为抛物线 的焦点,过P的直线l与抛物线交与A,B两点,若Q在直线l上,且满足
的焦点,过P的直线l与抛物线交与A,B两点,若Q在直线l上,且满足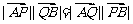 ,则点Q总在定直线
,则点Q总在定直线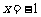 上.试猜测如果P为椭圆
上.试猜测如果P为椭圆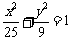 的左焦点,过P的直线l与椭圆交与A,B两点,若Q在直线l上,且满足
的左焦点,过P的直线l与椭圆交与A,B两点,若Q在直线l上,且满足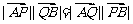 ,则点Q总在定直线
▲ 上.
,则点Q总在定直线
▲ 上.
8、已知 ,设函数
,设函数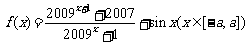 的最大值为
的最大值为 ,最小值为
,最小值为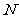 ,那么
,那么 ▲ .
▲ .
7、动点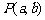 在不等式组
在不等式组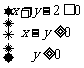 表示的平面区域内部及其边界上运动,则
表示的平面区域内部及其边界上运动,则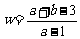 的取值范围是 ▲ .
的取值范围是 ▲ .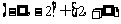
6、若数列 满足
满足 (
(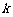 为常数),则称数列
为常数),则称数列 为等比和数列,k称为公比和.已知数列
为等比和数列,k称为公比和.已知数列 是以3为公比和的等比和数列,其中
是以3为公比和的等比和数列,其中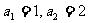 ,则
,则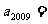 ▲ .
▲ .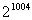
5、从某项综合能力测试中抽取100人的成绩,统计如下表,则这100人成绩的标准差为 ▲ .3
|
分数 |
5 |
4 |
3 |
2 |
1 |
|
人数 |
20 |
10 |
30 |
30 |
10 |
4、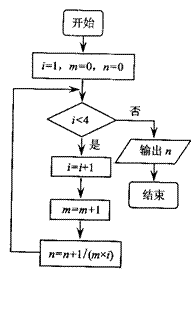 下右图是一个算法的程序框图,该算法所输出的结果是 ▲ .
下右图是一个算法的程序框图,该算法所输出的结果是 ▲ .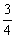
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com