
1.“低能耗”、“低废水”、“低废弃物”是低碳理念的重要内涵。下列做法不符合低碳理念的是
A.推广利用太阳能 B.家庭电器长期处于待机状态
C.循环使用生活用水 D.回收有机垃圾用于生产沼气
22.
解:⑴ ∵二次函数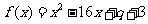 的对称轴是
的对称轴是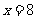
∴函数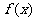 在区间
在区间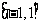 上单调递减
2分
上单调递减
2分
∴要函数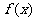 在区间
在区间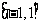 上存在零点须满足
上存在零点须满足
即 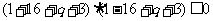 4分
4分
解得 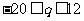 6分
6分
⑵ 当 时,即
时,即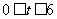 时,
时,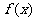 的值域为:
的值域为: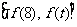 ,即
,即 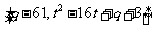
∴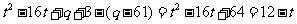
∴ ∴
∴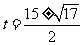 ,经检验
,经检验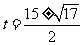 不合题意,舍去。
8分
不合题意,舍去。
8分
当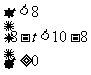 时,即
时,即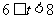 时,
时,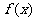 的值域为:
的值域为: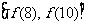 ,即
,即 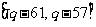
∴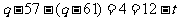 ∴
∴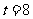
经检验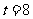 不合题意,舍去。
10分
不合题意,舍去。
10分
当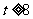 时,
时,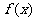 的值域为:
的值域为: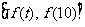 ,即
,即 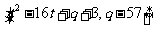
∴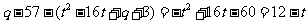
∴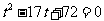 ∴
∴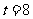 或
或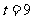
经检验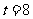 或
或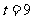 满足题意,
12分
满足题意,
12分
所以存在常数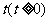 ,当
,当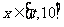 时,
时,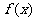 的值域为区间
的值域为区间 ,且
,且 的长度为
的长度为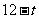 。14分
。14分
21.
解 (1)依题得:
 4分
4分
(2)(Ⅰ)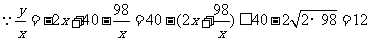
当且仅当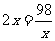 时,即x=7时等号成立.¥高#考#资%源*网
时,即x=7时等号成立.¥高#考#资%源*网
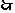 到2008年,年平均盈利额达到最大值,工厂共获利12×7+30=114万元. 8分
到2008年,年平均盈利额达到最大值,工厂共获利12×7+30=114万元. 8分
(Ⅱ)y=-2x2+40x-98=-(x-10)2+102,当x=10时,ymax=102
故到2011年,盈利额达到最大值,工厂获利102+12=114万元 11分
盈利额达到的最大值相同,而方案Ⅰ所用的时间较短,故方案Ⅰ比较合理.12分
19.解:因为方程x 2 + mx + 1=0有两个不相等的实根,
所以Δ1=m 2 – 4>0, ∴m>2或m < – 2 …………3分
又因为不等式4x 2 +4(m – 2)x + 1>0的解集为R,
所以Δ2=16(m – 2) 2– 16<0, ∴1< m <3 …………6分
因为p或q为真,p且q为假,所以p与q为一真一假, …………8分
(1)当p为真q为假时, …………10分
…………10分
(2)当p为假q为真时,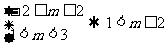
综上所述得:m的取值范围是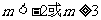 或
或 …………12分
…………12分
18.

22.(本小题满分14分)
已知二次函数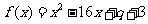 :
:
⑴若函数在区间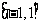 上有零点,求实数
上有零点,求实数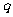 的取值范围;
的取值范围;
⑵问:是否存在常数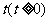 ,当
,当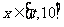 时,
时,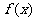 的值域为区间
的值域为区间 ,且
,且 的长度为
的长度为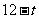 。
。
21.(本小题满分12分)
某机床厂今年年初用98万元购进一台数控机床,并立即投入生产使用,计划第一年维修、保养费用12万元,从第二年开始,每年所需维修、保养费用比上一年增加4万元,该机床使用后,每年的总收入为50万元,设使用x年后数控机床的盈利额为y万元.
(1)写出y与x之间的函数关系式;
(2)使用若干年后,对机床的处理方案有两种:(Ⅰ)当年平均盈利额达到最大值时,以30万元价格处理该机床;(Ⅱ)当盈利额达到最大值时,以12万元价格处理该机床.请你研究一下哪种方案处理较为合理?请说明理由.
20.(本小题满分12分)
函数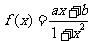 是定义在(-1,1)的奇函数,且
是定义在(-1,1)的奇函数,且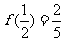 。
。
(1)确定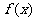 的解析式;(2)判断函数在(-1,1)上的单调性;
的解析式;(2)判断函数在(-1,1)上的单调性;
(3)解不等式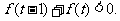
19.(本小题满分12分)
已知命题p:方程x 2 +mx+1=0有两个不相等的实根;
q:不等式4x 2+4(m-2)x +1>0的解集为R;若p或q为真,p且q为假,求实数m的取值范围
18.(本小题满分12分)
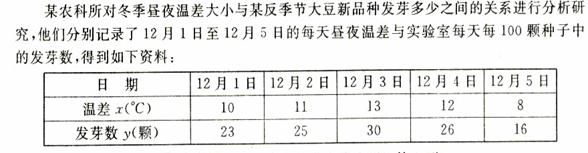
该农科所确定的研究方案是:先从这五组数据中选取2组,用剩下的3组数据求线性回归方程,
再对被选取的2组数据进行检验.
(1)若选取的是12月1日与12月5日的两组数据,请根据12月2日至12月4日的数据,
求出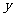 关于
关于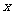 的线性回归方程
的线性回归方程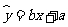 ;
;
(2)若由线性回归方程得到的估计数据与所选出的检验数据的误差均不超过2颗,则认为得到的线性回归方程是可靠的,试问(1)中所得的线性回归方程是否可靠
(参考公式: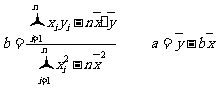 )
)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com