
17.(本小题满分12高☆考♂资♀源*网分)
已知函数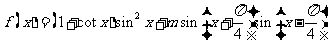 。
。
(1) 当m=0时,求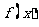 在区间
在区间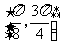 上的取值范围;
上的取值范围;
(2) 当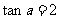 时,
时,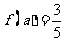 ,求m的值。
,求m的值。
[解析]考查三角函数的化简、三角函数的图像和性质、已知三角函数值求值问题。依托三角函数化简,考查函数值域,作为基本的知识交汇问题,考查基本三角函数变换,属于中等题.
解:(1)当m=0时,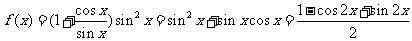
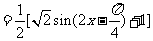 ,由已知
,由已知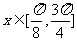 ,得
,得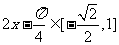
从而得: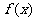 的值域为
的值域为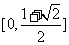
(2)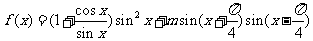
化简得: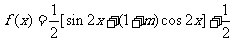
当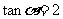 ,得:
,得: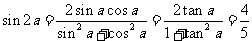 ,
,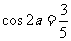 ,
,
代入上式,m=-2.
16.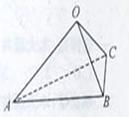 如图,在三棱锥
如图,在三棱锥 中,三条棱
中,三条棱 ,
, ,
,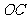 两两垂直,且
两两垂直,且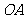 >
>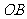 >
>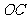 ,分别经过三条棱
,分别经过三条棱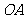 ,
,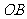 ,
,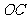 作一个截面平分三棱锥的体积,截面面积依次为
作一个截面平分三棱锥的体积,截面面积依次为 ,
,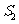 ,
,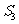 ,则
,则 ,
,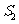 ,
,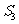 的大小关系为
。
的大小关系为
。
[答案] 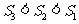
[解析]考查立体图形的空间感和数学知识的运用能力,通过补形,借助长方体验证结论,特殊化,令边长为1,2,3得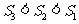 。
。
15.点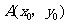 在双曲线
在双曲线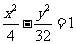 的右支上,若点A到右焦点的距离等于
的右支上,若点A到右焦点的距离等于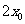 ,则
,则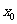 =
=
[答案] 2
[解析]考查圆锥曲线的基本概念和第二定义的转化,读取a=2.c=6,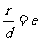
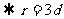 ,
,

14.将6位志愿者分成4组,其中两个各2人,另两个组各1人,分赴世博会的四个不同场馆服务,不同的分配方案有 种(用数字作答)。
[答案] 1080
[解析]考查概率、平均分组分配问题等知识,重点考查化归转化和应用知识的意识。先分组,考虑到有2个是平均分组,得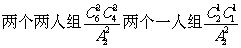 ,再全排列得:
,再全排列得:
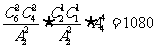
高☆考♂资♀源*网
13.已知向量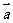 ,
,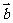 满足
满足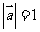 ,
,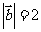 ,
, 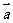 与
与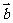 的夹角为60°,则
的夹角为60°,则
[答案] 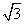
[解析]考查向量的夹角和向量的模长公式,以及向量三角形法则、余弦定理等知识,如图 ,由余弦定理得:
,由余弦定理得:
12. 如图,一个正五角星薄片(其对称轴与水面垂直)匀速地升出水面,记t时刻五角星露出水面部分的图形面积为
如图,一个正五角星薄片(其对称轴与水面垂直)匀速地升出水面,记t时刻五角星露出水面部分的图形面积为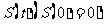 ,则导函数
,则导函数 的图像大致为
的图像大致为
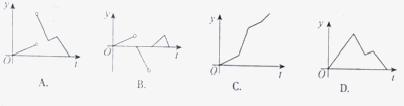
[答案]A
[解析]本题考查函数图像、导数图、导数的实际意义等知识,重点考查的是对数学的探究能力和应用能力。最初零时刻和最后终点时刻没有变化,导数取零,排除C;总面积一直保持增加,没有负的改变量,排除B;考察A、D的差异在于两肩位置的改变是否平滑,考虑到导数的意义,判断此时面积改变为突变,产生中断,选择A。
 高☆考♂资♀源*网
高☆考♂资♀源*网
11.一位国王的铸币大臣在每箱100枚的硬币中各掺入了一枚劣币,国王怀疑大臣作弊,他用两种方法来检测。方法一:在10箱子中各任意抽查一枚;方法二:在5箱中各任意抽查两枚。国王用方法一、二能发现至少一枚劣币的概率分别为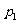 和
和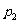 ,则
,则
A. 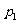 =
=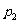 B.
B. 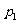 <
<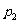 C.
C. 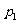 >
>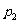 D。以上三种情况都有可能
D。以上三种情况都有可能
[答案]B
[解析]考查不放回的抽球、重点考查二项分布的概率。本题是北师大版新课标的课堂作业,作为旧大纲的最后一年高考,本题给出一个强烈的导向信号。方法一:每箱的选中的概率为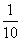
,总概率为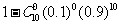 ;同理,方法二:每箱的选中的概率为
;同理,方法二:每箱的选中的概率为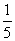 ,总事件的概率为
,总事件的概率为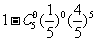 ,作差得
,作差得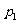 <
<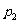 。
。
10.过正方体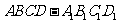 的顶点A作直线L,使L与棱
的顶点A作直线L,使L与棱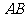 ,
,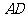 ,
,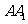 所成的角都相等,这样的直线L可以作
所成的角都相等,这样的直线L可以作
A.1条 B.2条 C.3条 D.4条
[答案]D
[解析]考查空间感和线线夹角的计算和判断,重点考查学生分类、划归转化的能力。第一类:通过点A位于三条棱之间的直线有一条体对角线AC1,第二类:在图形外部和每条棱的外角和另2条棱夹角相等,有3条,合计4条。
9.给出下列三个命题:
①函数 与
与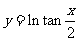 是同一函数;高☆考♂资♀源*网
是同一函数;高☆考♂资♀源*网
②若函数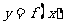 与
与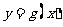 的图像关于直线
的图像关于直线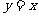 对称,则函数
对称,则函数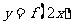 与
与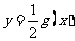 的图像也关于直线
的图像也关于直线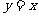 对称;
对称;
③若奇函数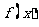 对定义域内任意x都有
对定义域内任意x都有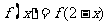 ,则
,则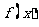 为周期函数。
为周期函数。
其中真命题是
A. ①② B. ①③ C.②③ D. ②
[答案]C
 [解析]考查相同函数、函数对称性的判断、周期性知识。考虑定义域不同,①错误;排除A、B,验证③,
[解析]考查相同函数、函数对称性的判断、周期性知识。考虑定义域不同,①错误;排除A、B,验证③,  ,又通过奇函数得
,又通过奇函数得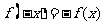 ,所以f(x)是周期为2的周期函数,选择C。
,所以f(x)是周期为2的周期函数,选择C。
高☆考♂资♀源*网
8.直线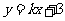 与圆
与圆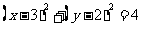 相交于M,N两点,若
相交于M,N两点,若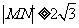 ,则k的取值范围是
,则k的取值范围是
A. 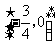 B.
B.
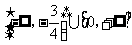 C.
C. 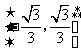 D.
D.
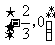
[答案]A
[解析]考查直线与圆的位置关系、点到直线距离公式,重点考察数形结合的运用.
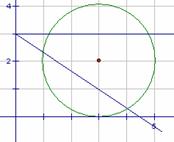 解法1:圆心的坐标为(3.,2),且圆与y轴相切.当
解法1:圆心的坐标为(3.,2),且圆与y轴相切.当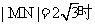 ,由点到直线距离公式,解得
,由点到直线距离公式,解得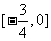 ;
;
解法2:数形结合,如图由垂径定理得夹在两直线之间即可, 不取 ,排除B,考虑区间不对称,排除C,利用斜率估值,选A
,排除B,考虑区间不对称,排除C,利用斜率估值,选A
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com