2、规律与应用

(1)性质强弱的规律

在“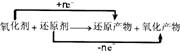”中，氧化性强弱顺序是：氧化剂>氧化产物；还原性

强弱顺序是：还原剂>还原产物。

　　 (2)守恒规律

　　 化合价有升必有降，电子有得必有失．对于一个完整的氧化还原反应，化合价升高总数与降低总数相等，失电子(或共用电子对偏离)总数与得电子(或共用电子对偏向)总数相等。

　　 (3)其他规律：价态表现性质规律，最高价态只有氧化性，最低价态只有还原性，中间价态既有氧化性又有还原性；转化规律，以元素相邻价态间的转化最容易；同种元素不同价态之间的氧化还原反应，化合价的变化遵循“只靠拢，不交叉”(即价态归中)；同种元素相邻价态间不发生氧化还原反应；反应先后的一般规律，在浓度相差不大的溶液中，同时含有几种还原剂时，若加入氧化剂，则它首先与溶液中还原性最强的还原剂作用。

　　 氧化还原反应贯穿于各章元素化合物的知识当中，是化学学科的支柱之一。因此在高考命题中，无论是选择题还是综合题都有关于氧化还原反应的试题。从考查的内容看，有考氧化还原概念的，有写氧化还原反应方程式的，有写氧化还原离子方程式的。突出能力的考查则要联系实际并写出教材中没有学过的氧化还原反应方程式，考氧化还原概念时也多采用学生没有学过的反应。

1、相关概念关系：

　　 阿伏加德罗常数受到历年高考选择题的青睐。最为常见的题干都是“NA表示阿伏加德罗常数，下列说法正确的是”。主要考查考生对物质的量、阿伏加德罗常数、摩尔质量、气体摩尔体积、物质的量浓度、阿伏加德罗定律等概念清楚辩析、灵活应用。这类题目是以阿伏加德罗常数为载体，考查内容涉及化学基本概念和基本理论、元素化合物甚至化学实验等多方面的知识。每年高考题目关于阿伏加德罗常数考点的设计给考生的感觉熟悉，但在历年高考中都有很好的区分度。考生失分的原因主要是缺少对于基础知识的全面理解和对常考易错点的归纳与概括。

　　 从历年高考题目不难发现，要准确解答此类题目，认真审题是关键。审题重点应该关注的是题干所设置的“陷阱”：

　　 最为常见的是条件陷阱，如气体体积是常温常压下的就不能用标准状况下的气体摩尔体积进行计算，标准状况下所给物质本身不是气态的如、水、辛烷、等。但要注意，气体的物质的量、质量与条件无关。如32克氧气无论在常温常压下还是标准状况下都是1摩尔。

　　 分子结构陷阱，稀有气体是单原子分子，臭氧是三原子分子，氢气、氮气等是双原子分子。在计算物质所含分子、原子、离子、中子、电子等的数目时应充分考虑物质结构，如过氧化钠中阴离子数目的求算等。

化学反应和隐含平衡的陷阱，如氧化还原反应的实质及电子转移的计算，与

存在的化学平衡，离子的水解、电离平衡等。

　　 只要概念清楚，分析问题会抓住本质，应对阿伏加德罗常数的选择题就会得心应手。

　　 　基本概念和基本理论在高考中的赋分比例约40%，虽较以前考纲规定的45%的比例略有降低，但丝毫不影响其作为高考中重大考查对象的地位。

　　 　与旧的课程体系相比，在复习中要特别注意新增知识点：难溶物质的溶解平衡、溶度积常数的应用[如09年高考化学广东第18题；福建第24题(5)]；平衡常数的计算或应用[如09年高考化学广东省第20题第(3)问；江苏化学的14题；上海化学第17题等]；盖斯定律的应用[如09年高考的广东化学第23题(1)；江苏化学第17题(2)]。

知识要点归纳：

11 已知平面直角坐标系中O是坐标原点，，圆是的外接圆，过点(2，6)的直线被圆所截得的弦长为.

(1)求圆的方程及直线的方程；

(2)设圆的方程，，过圆上任意一点作圆的两条切线，切点为，求的最大值.

12．已知各项均为实数的数列{a_n}是公差为d的等差数列，它的前n项和为S_n，且满足S₄＝2S₂+8．

(1)求公差d的值；

(2)若数列{a_n}的首项的平方与其余各项之和不超过10，则这样的数列至多有多少项；

(3)请直接写出满足(2)的项数最多时的一个数列(不需要给出演算步骤)．

22．(本题满分14分)

已知椭圆经过点，长轴长为，设过右焦点F斜率为k的直线交椭圆M于A、B两点。

　 (1)求椭圆M的方程；

　 (2)设过右焦点F且与直线AB垂直的直线交椭圆M于C、D，求|AB|+|CD|的最小值。

21．(本题满分12分)

　　 已知二次函数对任意实数x都满足且

　 (1)求的表达式；

　 (2)设求证：上为减函数；

　 (3)在(2)的条件下，证明：对任意，恒有

20．(本题满分12分)

四棱锥P-ABCD中，底面ABCD是矩形，又PA=PD，E是BC的中点。

　 (1)求证：AD⊥PE；

　 (2)在PA上是否存在一点M，使ME//平面PDC？

19．(本题满分12分)

某高级中学共有学生2000人，各年级男、女生人数如下表：

年级 性别	高一	高二	高三
女生	373	x	y
男生	377	370	z

已知在全学校学生中随机抽取1名，抽到高二年级女生的概率是0.19。

　 (1)现用分层抽样的方法在全校抽取48名学生，问应在高三年级抽取多少人？

　 (2)已知求高三年级女生比男生多的概率。

18．(本题满分12分)

在数列中，

　 (1)求的值；

　 (2)证明：数列是等比数列，并求的通项公式；

　 (3)求数列的前n项和