

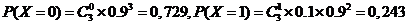
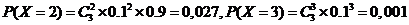
故随机变量X的分布列为
|
X |
0 |
1 |
2 |
3 |
|
P |
0.729 |
0.243 |
0.027 |
0.001 |
X的数学期望为EX=3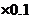 =0.3
=0.3
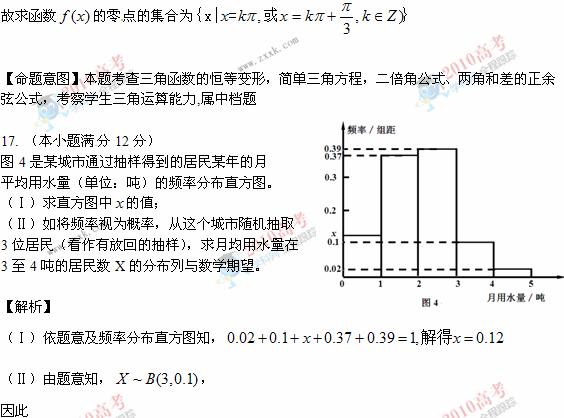
[命题意图]本题考查频率分布直方图、二项分布、离散型随机变量的分布列与数学期望。属中档题
18.(本小题满 分12分)
分12分)
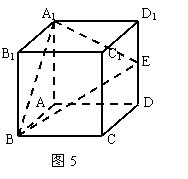
如图5所示,在正方体ABCD-A1B1C1D1中,E是棱DD 1的中点。
1的中点。
 (Ⅰ)求直线BE与平面ABB1A1所成的角的正弦值;
(Ⅰ)求直线BE与平面ABB1A1所成的角的正弦值;
(Ⅱ)在棱C1D1上是否存在一点F,使B1F//平面A1BE?证明你的结论。
[解析]

所以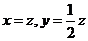 ,取
,取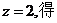 n
n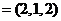 .
.
设F是棱C1D1上的点,则F(t,1,1)(0≤t≤1),又B1(1,0,1),所以
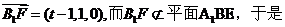
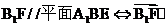 n
n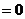
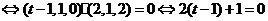
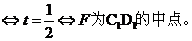 这说明在在棱C1D1上是否存在一点F(
这说明在在棱C1D1上是否存在一点F(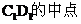 ),使B1F//平面A1BE
),使B1F//平面A1BE
解法2 如图(a)所示,取AA1的中点M,连结EM,BM,因为E是DD1的中点,四边形ADD1A1为正方形,所以EM//AD。
又在正方体ABCD-A1B1C1D1中。AD⊥平面ABB1A1,所以EM⊥ABB1A1,从而BM为直线BE在平面ABB1A1上的射影,∠EBM直线BE与平面ABB1A1所成的角.
设正方体的棱长为2,则EM=AD=2,BE=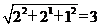 ,于是
,于是
在RT△BEM中,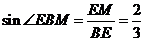
15.若数列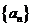 满足:对任意的
满足:对任意的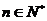 ,只有有限个正整数
,只有有限个正整数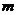 使得
使得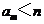 成立,记这样的
成立,记这样的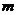 的个数为
的个数为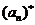 ,则得到一个新数列
,则得到一个新数列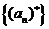 .例如,若数列
.例如,若数列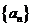 是
是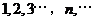 ,则数列
,则数列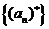 是
是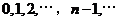 .已知对任意的
.已知对任意的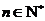 ,
,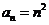 ,则
,则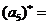 ,
,
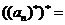
 .
.
[答案]2,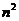
[解析]因为 ,而
,而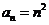 ,所以m=1,2,所以
,所以m=1,2,所以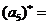 2.
2.
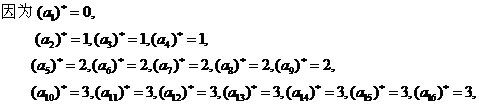
所以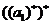 =1,
=1, 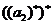 =4,
=4,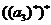 =9,
=9,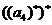 =16,
=16,
猜想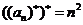
[命题意图]本题以数列为背景,通过新定义考察学生的自学能力、创新能力、探究能力,属难题。
11.在区间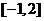 上随机取一个数x,则
上随机取一个数x,则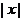 ≤1的概率为________.
≤1的概率为________.
[答案]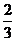
[解析]P(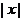 ≤1)=
≤1)=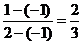
 [命题意图]本题考察几何概率,属容易题。
[命题意图]本题考察几何概率,属容易题。
 [解析]抛物线的焦点坐标为F(0,
[解析]抛物线的焦点坐标为F(0,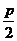 ),则过焦点斜率为1的直线方程为
),则过焦点斜率为1的直线方程为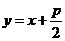 ,
,
设A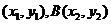 (
(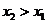 ),由题意可知
),由题意可知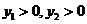
由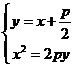 ,消去y得
,消去y得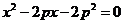 ,
,
由韦达定理得,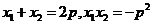
所以梯形ABCD的面积为:
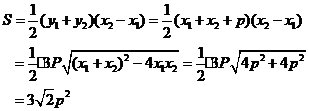
所以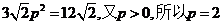
[命题意图]本题考查抛物线的焦点坐标,直线的方程,直线与抛物线的位置关系,考察考生的运算能力,属中档题
10.如图1所示,过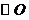 外一点P作一条直线与
外一点P作一条直线与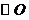 交于A,B两点,已知PA=2,点P到
交于A,B两点,已知PA=2,点P到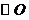 的切线长PT =4,则弦AB的长为________.
的切线长PT =4,则弦AB的长为________.
[答案]6
[解析]根据切线长 定理
定理
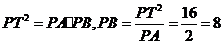
所以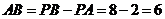
[命题意图]本题考察平面几何的切线长定理,属容易题。
9. 已知
已知 一种材料的最佳加入量在110g到210 g之间,若用0.618法安排试验,则第一次试点的加入量可以是_____________g.
一种材料的最佳加入量在110g到210 g之间,若用0.618法安排试验,则第一次试点的加入量可以是_____________g.
[答案]171.8或148.2
[解析 ]根据0.618法,第一次试点加入量为
]根据0.618法,第一次试点加入量为
110+(210-110)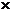 0.618=171.8
0.618=171.8
或 210-(210-110)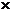 0.618=148.2
0.618=148.2
[命题意图]本题考察优选法的0.618法,属容易题。
7.在某种信息传输过程中,用4个数字的一个排列(数字也许重复)表示一个信息,不同排列表示不同信息,若所用数字只有0和1,则与信息0110至多有两个对应位置上的数字相同的信息个数为
A.10 B.11 C.12 D.15
[答案]B
[解析]与信息0110至多有两个对应位置上的数字相同的信息包括三类:
第一类:与信息0110有两个对应位置上的数字相同有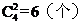

[命题意图]本题通过新定义考察学生的创新能力,考察函数的图象,考察考生数形结合的能力,属中档题。
2.下列命题中的假命题是
A.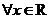 ,
,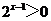
 B.
B.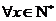 ,
,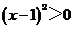 [
[
C.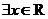 ,
,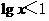 D.
D.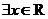 ,
,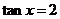
[答案]B
 [解析]对于B选项x=1时,
[解析]对于B选项x=1时,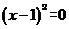 ,故选B.
,故选B.


[命题意图]本题考查余弦定理,特殊角的三角函数值,不等式的性质,比较法,属中档题。
1.已知集合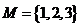 ,
,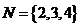 ,则
,则
A.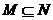
 B.
B.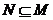
C.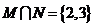 D.
D.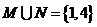
[答案]C
[解析]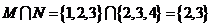 故选C.
故选C.
[命题意图]本题考查集合的交集与子集的运算,属容易题.
12.如图9-2-26所示,电阻不计的平行金属导轨MN和OP放置在水平面内.MO间接有阻值为R=3 Ω的电阻.导轨相距d=1 m,其间有竖直向下的匀强磁场,磁感应强度B=0.5 T.质量为m=0.1 kg,电阻为r=1 Ω的导体棒CD垂直于导轨放置,并接触良好.用平行于MN的恒力F=1 N向右拉动CD.CD受摩擦阻力f恒为0.5 N.求:
(1)CD运动的最大速度是多少?
(2)当CD到最大速度后,电阻R消耗的电功率是多少?
(3)当CD的速度为最大速度的一半时,CD的加速度是多少?
解析:(1)设CD棒运动速度为v,则:导体棒产生的感应电动势为:E=Bdv①
据闭合电路欧姆定律有:I=②
则安培力为:F0=BdI③
据题意分析,当v最大时,有:F-F0-Ff=0④
联立①②③④得:vm==8 m/s.⑤
(2)棒CD速度最大时同理有:Em=Bdvm⑥
Im=⑦
而PRm=I·R⑧
联立⑤⑥⑦得:PRm==3 W.⑨
(3)当CD速度为vm时有:E′=Bdvm/2⑩
I=⑪
F′=BId⑫
据牛顿第二定律有:F-F′-Ff=ma⑬
联立⑩⑪⑫⑬⑭得:a=2.5 m/s2.⑭
答案:(1)8 m/s (2)3 W (3)2.5 m/s2
11.如图9-2-25所示,矩形导线圈边长分别为L1、L2,共有N匝,内有一匀强磁场,磁场方向垂直于线圈所在平面向里,线圈通过导线接一对水平放置的平行金属板,两板间的距离为d,板长为L0.t=0时,磁场的磁感应强度B从B0开始均匀变化,同时一带电荷量为+q、质量为m的粒子从两板间的中点以水平初速度v0向右进入两板间,不计重力,若该粒子恰能从上板的右端射出,则:
(1)磁感应强度随时间的变化率k多大?
(2)磁感应强度B与时间t应满足什么关系?
(3)两板间电场对带电粒子做的功为多少?
解析:(1)线圈中产生的感应电动势大小:E=N=NL1L2=NL1L2k
两板间电压:U=E,粒子在两板间的加速度:a==
设粒子通过平行金属板的时间为t0,则有:L=v0t0,=at,联立解得:k=.
(2)由题意可知磁感应强度是逐渐增大的,则有:B=B0+t.
(3)电场力对带电粒子所做的功为W=qU,联立解得:W=.
答案:(1) (2)B0+t (3)
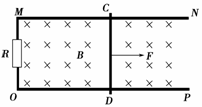
图9-2-26
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com