1．设集合，集合，则AB= ( 　 )

(A)()　　　 (B)　　 　(C)[]　　　 (D)

22．(本小题满分12分)

已知函数f(x)＝(1+x)²－4a lnx(a∈N﹡)．

(Ⅰ)若函数f(x)在(1，+∞)上是增函数，求a的高*考#资^源*网值；

(Ⅱ)在(Ⅰ)的高*考#资^源*网条件下，若关于x的高*考#资^源*网方程f(x)＝x²－x+b在区间[1，e]上恰有一个实根，求实数b的高*考#资^源*网取值范围．

21．(本小题满分12分)

过抛物线y²＝2px(p>0)的高*考#资^源*网对称轴上的高*考#资^源*网定点

M(m，0)(m>0)，作直线AB与抛物线相交于A、B两点．

(Ⅰ)试证明A、B两点的高*考#资^源*网纵坐标之积为定值；

(Ⅱ)若点N(－m，2m)，求直线AN、BN的高*考#资^源*网斜率

之和．

20．(本小题满分12分)

已知数列{}的高*考#资^源*网前n项和为，且满足a₁＝1，t－(2t+1)＝t，其中t>0，n∈N﹡，n≥2．

(Ⅰ)求证：数列{}是等比数列；

(Ⅱ)设数列{}的高*考#资^源*网公比为f(t)数列{}满足b₁＝1，＝f()(n≥2)，求数列{}的高*考#资^源*网通项公式；

(Ⅲ)在(Ⅱ)的高*考#资^源*网条件下，若t＝1，数列{}的高*考#资^源*网前n项和为，试比较和的高*考#资^源*网大小关系．

19．(本小题满分12分)

已知斜三棱柱ABC－A₁B₁C₁的高*考#资^源*网侧面A₁ACC₁与底面ABC垂直，∠ABC＝90°，BC＝2，AC＝2，且AC＝AA₁＝A₁C．

(Ⅰ)求侧棱AA₁与底面ABC所成角的高*考#资^源*网大小；

(Ⅱ)求侧面A₁ABB₁与底面ABC所成二面角的高*考#资^源*网正切值；

(Ⅲ)求顶点C到侧面A₁ABB₁的高*考#资^源*网距离．

18．(本小题满分12分)

某种项目的高*考#资^源*网射击比赛，开始时在距目标100m处射击，如果命中记6分，且停止射击；若第一次射击未命中，可以进行第二次射击，但目标已经在150m处，这时命中记3分，且停止射击；若第二次仍未命中，还可以进行第三次射击，此时目标已经在200m处，若第三次命中则记1分，并停止射击；若三次都未命中，则记0分，且不再继续射击．已知射手甲在100m处击中目标的高*考#资^源*网概率为，他的高*考#资^源*网命中率与其距目标距离的高*考#资^源*网平方成反比，且各次射击是否击中目标是相互独立的高*考#资^源*网．

(Ⅰ)分别求这名射手在150m处、200m处的高*考#资^源*网命中率；

(Ⅱ)设这名射手在比赛中得分数为ξ，求随机变量ξ的高*考#资^源*网分布列和数学期望．

17．(本小题满分10分)

已知函数f(x)＝Asin(ωx+)+B(A>0，ω>0，0≤<2π)在同一周期内有最高点(，1)和最低点(，－3)．

(Ⅰ)求函数y＝f(x)的高*考#资^源*网解析式；

(Ⅱ)画出函数y＝f(x)在区间[0，π]上的高*考#资^源*网图象．

16．已知函数f(x)＝｜x²－2ax+b｜(x∈R)，给出下列命题：

①f(x)必是偶函数； ②当f(0)＝f(2)时，f(x)的高*考#资^源*网图像必关于直线x＝1对称；③若a²－b≤0，则f(x)在区间[a，+∞)上是增函数；④f(x)有最大值为｜a²－b｜．其中正确命题的高*考#资^源*网序号是______________．

15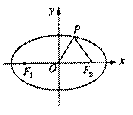．如图，F₁、F₂分别为椭圆(a>b>0)的高*考#资^源*网左、右焦点，点P在椭圆上，△POF₂是面积为的高*考#资^源*网正三角形，则b²的高*考#资^源*网值是__________________.

14．设集合A＝{(x，y)｜x，y，1－x－y是三角形的高*考#资^源*网三边长}，则集合A所表示的高*考#资^源*网平面区域的高*考#资^源*网面积是_______________．