2.(天津卷)下列关于原子和原子核的说法正确的是

A．β衰变现象说明电子是原子核的组成部分

B．波尔理论的假设之一是原子能量的量子化

C．放射性元素的半衰期随温度的升高而变短

D．比结合能越小表示原子核中的核子结合得越牢固

答案：B

8.(上海物理) 某放射性元素经过11.4天有的原子核发生了衰变，该元素的半衰期为

(A)11.4天　　　　　 (B)7.6天　　　　 (C)5. 7天　　　　　 (D)3.8天

答案：D

解析：根据，，因为t=11.4day，所以=3.8day，选D。

本题考查原子核半衰期的计算。

难度：中等。

4.(上海物理)现已建成的核电站的能量来自于

(A)天然放射性元素衰变放出的能量　　　　 (B)人工放射性同位素放出的的能量

(C)重核裂变放出的能量　　　　　　　　　 (D)化学反应放出的能量

答案：C

解析：本题考查原子核反应。

难度：易。

1．(上海物理)卢瑟福提出了原子的核式结构模型，这一模型建立的基础是

(A)粒子的散射实验　　　　　　　　　　　 (B)对阴极射线的研究

(C) 天然放射性现象的发现　　　　　　　　　 (D)质子的发现

答案：A

解析：卢瑟福根据α粒子的散射实验结果，提出了院子的核式结构模型：原子核聚集了院子的全部正电荷和几乎全部质量，电子在核外绕核运转。

本题考查原子的核式结构的建立。

难度：易。

15．(北京卷)太阳因核聚变释放出巨大的能量，同时其质量不断减少。太阳每秒钟辐射出的能量约为4×10²⁶J，根据爱因斯坦质能方程，太阳每秒钟减少的质量最接近

A．10³⁶Kg　　B．10¹⁸ Kg　　C．10¹³ Kg　　D．10⁹ Kg

答案：D

[解析]根据爱因斯坦的只能方程，，D正确。

13．(北京卷)属于狭义相对论基本假设的是：在不同的惯性系中，

　　 A．真空中光速不变　　　B．时间间隔具有相对性

　　 C．物体的质量不变　　　D．物体的能量与质量成正比

答案：A

34.(新课标卷)[物理--选修3-5]

　　 (1)(5分)用频率为的光照射大量处于基态的氢原子，在所发射的光谱中仅能观测到频率分别为的三条谱线，且，则_______.(填入正确选项前的字母)

　　 A、　　 B、　　 C、　　 D、

　　 答案：B

解析：大量氢原子跃迁时只有三个频率的光谱，这说明是从n=3能级向低能级跃迁，根据能量守恒有，，解得：，选项B正确。

14.(全国卷2)　 原子核与氘核反应生成一个α粒子和一个质子。由此可知

　　 A．A=2，Z=1　　 B. A=2，Z=2　　 C. A=3，Z=3　　 D. A=3，Z=2

[答案]D

[解析]，应用质量数与电荷数的守恒，解得，答案D。

[命题意图与考点定位]主要考查根据原子核的聚变反应方程，应用质量数与电荷数的守恒分析解决。

14．(全国卷1)原子核经放射性衰变①变为原子核，继而经放射性衰变②变为原子核，再经放射性衰变③变为原子核。放射性衰变　①、②和③依次为

A．α衰变、β衰变和β衰变　　 B．β衰变、β衰变和α衰变

C．β衰变、α衰变和β衰变　　 D．α衰变、β衰变和α衰变

[答案]A

[解析],质量数少4,电荷数少2,说明①为α衰变. ,质子数加1,说明②为β衰变,中子转化成质子. ,质子数加1,说明③为β衰变,中子转化成质子.

[命题意图与考点定位]主要考查根据原子核的衰变反应方程，应用质量数与电荷数的守恒分析解决。

24.(安徽卷)(20分)如图，ABD为竖直平面内的光滑绝缘轨道，其中AB段是水平的，BD段为半径R=0.2m的半圆，两段轨道相切于B点，整个轨道处在竖直向下的匀强电场中，场强大小E=5.0×10³V/m。一不带电的绝缘小球甲，以速度υ₀沿水平轨道向右运动，与静止在B点带正电的小球乙发生弹性碰撞。已知甲、乙两球的质量均为m=1.0×10^-2kg，乙所带电荷量q=2.0×10^-5C，g取10m/s²。(水平轨道足够长，甲、乙两球可视为质点，整个运动过程无电荷转移)

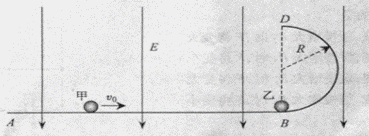
(1) 甲乙两球碰撞后，乙恰能通过轨道的最高点D，求乙在轨道上的首次落点到B点的距离；

(2)在满足(1)的条件下。求的甲的速度υ₀；

(3)若甲仍以速度υ₀向右运动，增大甲的质量，保持乙的质量不变，求乙在轨道上的首次落点到B点的距离范围。

答案：(1)0.4m　　 (2)　　 (3)＜＜

解析：

(1)在乙恰好能通过轨道的最高点的情况下，设乙到达最高点的速度为，乙离开D点达到水平轨道的时间为t，乙的落点到B点的距离为，则

　　　　　　　　　　　　　　　　　 ①

　　　　　　　　　　　　　　　　 ②

　　　　　　　　　　　　　　　　　　　　　　 ③

联立①②③得：　　　　　　　　　　　　　　 ④

(2)设碰撞后甲、乙的速度分别为、，根据动量守恒和机械能守恒定律有：

　　 　　　　　　　　　　　　　　　　⑤

　　 　　　　　　　　　　　　⑥

联立⑤⑥得：　　　　　　　　　　　　　　　　 ⑦

由动能定理得：　 ⑧

联立①⑦⑧得：　　　　　 ⑨

(3)设甲的质量为M，碰撞后甲、乙的速度分别为、，根据动量守恒和机械能守恒定律有：

　　 　　　　　　　　　　　　　　　　(10)

　　 　　　　　　　　　　　　(11)

联立(10)(11)得：　　　　　　　　　　　 (12)

由(12)和，可得：＜　　　　　　　　 (13)

设乙球过D点的速度为，由动能定理得

　　 　　　　　　　　　(14)

联立⑨(13)(14)得：＜　　　　　　　　　 (15)

设乙在水平轨道上的落点到B点的距离为，则有

　　 　　　　　　　　　　　　　　　　　　　　　　　(16)

联立②(15)(16)得：＜＜