
19.(本小题满分12分)
已知某地今年年初拥有居民住房的总面积为a(单位:m2),其中有部分旧住房需要拆除。当地有关部门决定每年以当年年初住房面积的10%建设新住房,同事也拆除面积为b(单位:m2)的旧住房。
(Ⅰ)分别写出第一年末和第二年末的实际住房面积的表达式:
(Ⅱ)如果第五年末该地的住房面积正好比今年年初的住房面积增加了30%,则每年拆除的旧住房面积b是多少?(计算时取1.15=1.6)

18.(本小题满分12分)
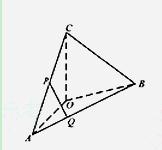
如图,在四面体ABOC中,OC⊥OA。OC⊥OB,∠AOB=120°,且OA=OB=OC=1
(Ⅰ)设P为AC的中点,Q在AB上且AB=3AQ,证明:PQ⊥OA;
(Ⅱ)求二面角O-AC-B的平面角的余弦值。

17.(本小题满分12分)
 为了了解一个小水库中养殖的鱼有关情况,从这个水库中多个不同位置捕捞出100条鱼,称得每条鱼的质量(单位:千克),并将所得数据分组,画出频率分布直方图(如图所示)
为了了解一个小水库中养殖的鱼有关情况,从这个水库中多个不同位置捕捞出100条鱼,称得每条鱼的质量(单位:千克),并将所得数据分组,画出频率分布直方图(如图所示)
(Ⅰ)在答题卡上的表格中填写相应的频率;
(Ⅱ)估计数据落在(1.15,1.30)中的概率为多少;
(Ⅲ)将上面捕捞的100条鱼分别作一记号后再放回水库,几天后再从水库的多处不同位置捕捞出120条鱼,其中带有记号的鱼有6条,请根据这一情况来估计该水库中鱼的总条数。

16.(本小题满分12分)
已经函数
(Ⅰ)函数 的图象可由函数
的图象可由函数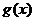 的图象经过怎样变化得出?
的图象经过怎样变化得出?
(Ⅱ)求函数 的最小值,并求使用
的最小值,并求使用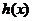 取得最小值的
取得最小值的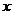 的集合。
的集合。

15.已知椭圆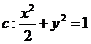 的两焦点为
的两焦点为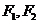 ,点
,点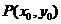 满足
满足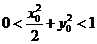 ,则|
,则|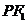 |+
|+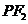 |的取值范围为_______,直线
|的取值范围为_______,直线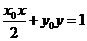 与椭圆C的公共点个数_____。
与椭圆C的公共点个数_____。
[答案]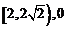
[解析]依题意知,点P 在椭圆内部.画出图形,由数形结合可得,当P在原点处时
在椭圆内部.画出图形,由数形结合可得,当P在原点处时 ,当P在椭圆顶点处时,取到
,当P在椭圆顶点处时,取到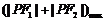 为
为
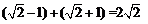
 ,故范围为
,故范围为 .因为
.因为 在椭圆
在椭圆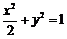 的内部,则直线
的内部,则直线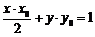 上的点(x, y)均在椭圆外,故此直线与椭圆不可能有交点,故交点数为0个.
上的点(x, y)均在椭圆外,故此直线与椭圆不可能有交点,故交点数为0个.
14.圆柱形容器内盛有高度为3cm的水,若放入三个相同的珠(球的半么与圆柱的底面半径相同)后,水恰好淹没最上面的球(如图所示),则球的半径是____cm.
[答案]4
[解析]设球半径为r,则 由
由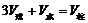 可得
可得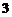
 ,解得r=4.
,解得r=4.
13.一个病人服用某种新药后被治愈的概率为0.9.则服用这咱新药的4个病人中至少3人被治愈的概率为_______(用数字作答)。
[答案]0.9744
[解析]分情况讨论:若共有3人被治愈,则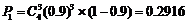 ;
;
若共有4人被治愈,则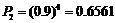 ,故至少有3人被治愈概率
,故至少有3人被治愈概率 .
.
12.已知: 式中变量
式中变量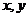 满足的束条件
满足的束条件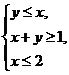 则z的最大值为______。
则z的最大值为______。
11.在 的展开中,
的展开中, 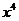 的系数为______。
的系数为______。
[答案]45
[解析]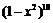 展开式即是10个(1-x2)相乘,要得到x4,则取2个1-x2中的(-x2)相乘,其余选1,则系数为
展开式即是10个(1-x2)相乘,要得到x4,则取2个1-x2中的(-x2)相乘,其余选1,则系数为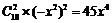 ,故
,故
 系数为45.
系数为45.
10.记实数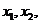 …
…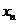 中的最大数为
中的最大数为 {
{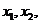 …
…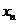 },最小数为min{
},最小数为min{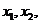 …
…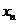 }.已知
}.已知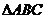 的三边边长为
的三边边长为 、
、 、
、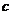 (
( ),定义它的倾斜度为
),定义它的倾斜度为
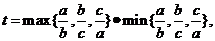
则“t=1”是“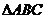 为等边三解形”的
为等边三解形”的
A,充分布不必要的条件 B.必要而不充分的条件
C.充要条件 D.既不充分也不必要的条件
[答案]B
[解析]若△ABC为等边三角形时,即a=b=c,则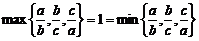 则l=1;若△ABC为等腰三角形,如a=2,b=
则l=1;若△ABC为等腰三角形,如a=2,b= 2,c=3时,
2,c=3时,
则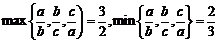 ,此时l=1仍成立但△ABC不为等边三角形,所以B正确.
,此时l=1仍成立但△ABC不为等边三角形,所以B正确.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com