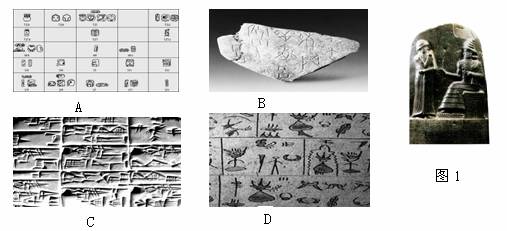
2、图1中的古代宝贵文献是得益于下列哪一文字而保留下来的　　　　　　　　　 (　　 )

1、历史学家马克布洛赫在《为历史学辩护》中说：“各时代的统一性是如此紧密，古今之间的关系是双向的。对现代的曲解必定源于对历史的无知；而对现实一无所知的人，要了解历史也必定是徒劳无功的。”布洛赫在此强调的是　 　　　　　　　　　 (　　 )

　　 A．鉴往知来　　　　　　　　　　　　　 B．以古讽今

　　 C．厚今薄古　　　　　　　　 　　　　　　D．贯通古今

21. (本小题满分14分)

已知函数f(x)=ax++c(a＞0)的图象在点(1,f(1))处的切线方程为y=x-1.

(Ⅰ)用a表示出b,c;

(Ⅱ)若f(x)＞㏑x在[1,∞]上恒成立，求a的取值范围；

(Ⅲ)证明：1+++…+＞㏑(n+1)+)(n≥1).

20. (本小题满分13分)

已知数列满足: ,　 , ；数列满足： =-(n≥1).

(Ⅰ)求数列，的通项公式;

(Ⅱ)证明:数列中的任意三项不可能成等差数列.

19. (本小题满分12分)

已知一条曲线C在y轴右边，C上没一点到点F(1,0)的距离减去它到y轴距离的差是1.

(Ⅰ)求曲线C的方程；

(Ⅱ)是否存在正数m，对于过点M(m,0)且与曲线C有连个交点A,B的任一直线，都有﹤0 ? 若存在，求出m的取值范围；若不存在，请说明理由.

18. (本小题满分12分)

　 如图, 在四面体ABOC中，OC⊥OA, OC⊥OB,∠AOB=120°，且OA=OB=OC=1.

(Ⅰ) 设P为AC的中点.证明：在AB上存在一点Q,使PQ⊥OA,并计算=的值；

(Ⅱ) 求二面角O-AC-B的平面角的余弦值. 　

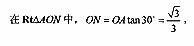
17．(本小题满分12分)

为了在夏季降温和冬季供暖时减少能源损耗，房屋的屋顶和外墙需要建造隔热层．某幢建筑物要建造可使用20年的隔热层，每厘米厚的隔热层建造成本为6万元．该建筑物每年的能源消耗费用C(单位：万元)与隔热层厚度(单位：cm)满足关系：，若不建隔热层，每年能源消耗费用为8万元．设为隔热层建造费用与20年的能源消耗费用之和．

(Ⅰ)求的值及的表达式；

(Ⅱ)隔热层修建多厚对，总费用达到最小，并求最小值．

16．(本小题满分12分)

已知函数，．

(Ⅰ)求函数的最小正周期；

(Ⅱ)求函数的最大值，并求使取得最大值的的集合．

15．设，称为a，b的调和平均数．如图，C为线殴AB上的点，且AC=a，CB=b，O为AB中点，以AB为直径作半圆．过点C作OD的垂线，垂足为E．连结OD，AD，BD．过点C作OD的垂线，垂足为E．则图中线段OD的长度是a，b的算术平均数，线段　　　 的长度是a，b的几何平均数，线段　　　 的长度是a，b的调和平均数．

[答案]CD　 CE

[解析]在Rt△ADB中DC为高，则由射影定理可得，故，即CD长度为a,b的几何平均数，将OC=代入可得故，所以ED=OD-OE=，故DE的长度为a,b的调和平均数.

14．某射手射击所得环数的分布列如下：

已知的期望，则y的值为　　　　 ．

[答案]0.4

[解析]由表格可知：

联合解得.