⑴ 集合，则=

　 (A) {1,2}　　 (B) {0,1,2}　　 (C){1,2,3}　　　 (D){0,1,2,3}

⑵在复平面内，复数6+5i, -2+3i 对应的点分别为A,B.若C为线段AB的中点，则点C对应的复数是

　 (A)4+8i　　 (B)8+2i　　 (C)2+4i　　　　 (D)4+i

⑶从{1,2,3,4,5}中随机选取一个数为a，从{1,2,3}中随机选取一个数为b，则b>a的概率是

　 (A)　　 (B)　　　 (C)　　　　 (D)

⑷若,是非零向量，且⊥，，则函数是

　 (A)一次函数且是奇函数　　　 (B)一次函数但不是奇函数

　 (C)二次函数且是偶函数　　　 (D)二次函数但不是偶函数

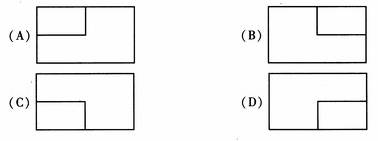
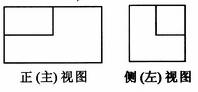(5)一个长方体去掉一个小长方体，所得几何体的

正视图与侧(左)视图分别如右图所示，则该集合体

的俯视图为：

　(6)给定函数①，②，③，④，期中在区间(0，1)上单调递减的函数序号是

(A)①②　 (B)②③　　 (C)③④　　 (D)①④

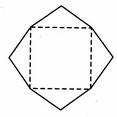(7)某班设计了一个八边形的班徽(如图)，它由腰长为1，

顶角为的四个等腰三角形，及其底边构成的正方形所组成，

该八边形的面积为

(A)；　　　　　　　 (B)

(C)　　　　　　　　 (D)

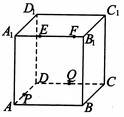
(8)如图，正方体的棱长为2，动点E、F在棱上。点Q是CD的中点，动点P在棱AD上，若EF=1，DP=x，E=y(x,y大于零)，

则三棱锥P-EFQ的体积：

(A)与x，y都有关；　　　　　　 (B)与x，y都无关；

(C)与x有关，与y无关；　　　　 (D)与y有关，与x无关；

第Ⅱ卷(共110分)

6.5g　 x　　　　 y　　　 z

解之得x=9.8g　　 y=16.1g　　　 z=0.2g

(1)稀中溶质的质量分数为=

(2)所得溶液中溶质的质量分数为=

答：(1)稀溶质的质量分数为6.5%。

(2)反应后所得溶液中溶质的质量分数为10.3%。

2. 加水稀释和配制溶液时，溶质的质量保持不变，因此，计算时，应以溶质质量不变为依据，建立等量关系。

设浓、稀溶液的质量分别为，溶质质量分数分别为a%、b%，混合后所得溶液质量和溶质质量分数分别为c和c%，则有，若是水和固体溶质混合溶解，它们的溶质质量分数可看作是0和100%。

[考点聚焦]

例1　 配制2000 mL 20%的稀硫酸()，需要98%的浓硫酸()多少毫升，水多少毫升？

分析　 解答此题应抓住两点：①稀释前后，溶质的质量不变；②两种液体或溶液混合，质量可以累加而体积不能累加，需将体积换算成质量。

解：设需加入浓体积为x，水的体积为y。

x=252.9mL

答：需要98%的浓硫酸252.9mL，水1814.7mL。

例2　 6.5g锌和150g稀恰好完全反应，求：(1)稀的溶质质量分数。(2)反应后所得溶液中溶质的质量分数。

分析　 解答本题关键是求出溶质和溶液的质量。反应后溶质应为。可根据质量守恒定律求得，溶液的质量=锌的质量+稀的质量－放出H₂的质量。

解：设稀含溶质的质量为x，生成的质量为y，生成的质量为z。

65　　 98　　　 161　　 2

1. 溶质的质量分数的计算，要扣紧它的数学表达式。围绕两个问题思考：一是溶质是什么物质；二是找出数学表达式中的三个值，即溶质的质量分数、溶质的质量、溶液或溶剂的质量，找出其中任意两个量，就可求出第三个量。此外，还要注意概念中的“质量”二字，计算时所用数据必须是质量，求出的结果也是质量。如果是体积，计算时，必须换成质量。

3. 溶液的稀释和混合的有关计算。

2. 计算配制一定量溶质质量分数的溶液，所需溶质、溶剂的质量。

1. 已知溶质、溶剂的质量，计算溶质的质量分数。

[重难点]

3. 变化关系：溶质的质量分数是由溶质质量和溶剂质量共同决定的，其中任何一个量发生改变时，其溶质的质量分数都会随着改变。

2. 表示方法：溶质的质量分数(ω)=。