19.　 (本小题满分12分)

设函数

(1)　　　 求的最小值；

(2)　　　 若对时恒成立，求实数的取值范围。

18.　 (本小题满分12分)

某公园有甲、乙两个相邻景点，原拟定甲景点内有2个A班同学和2个B班同学；乙景点内有2个A班同学和3个B班同学，后由于某种原因，甲、乙两景点各有一个同学交换景点观光。

(1)　　　 求甲景点恰有2个A班同学的概率；

(2)　　　 求甲景点A班同学数的分布列及数学期望。

17.　 (本小题满分12分)

设向量，函数

(1)　　　 求函数的最小正周期；

(2)　　　 当时，求函数的值域；

(3)　　　 求使不等式成立的的取值范围。

16.　 已知点的坐标满足条件点为，那么的取值范围为　　　

15.　 设函数是定义在上的奇函数，若当时，,则满足的的取值范围是　　　

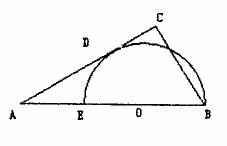
14.　 如图，已知是半圆的直径，是延长线上一点，切半圆于点,于，若，则　　　; 　　　

13.　 在正三棱柱，若，则到平面的距离　　　

12.　 极坐标系下，曲线与曲线的公共点个数是　　　

11.　 电动自行车的耗电量与速度这间的关系为，为使耗电量最小，则其速度应定为　　　

10.　 曲线(为参数)上各点到直线的最大距离是

A. 　　B. 　　　C. 　　D.

第Ⅱ卷(共100分)

第Ⅱ卷共2页。考生必须使用0.5毫米黑色签字笔在答题卡上个题目的指定答题区域内作答，填空题请直接写答案，解答题应写出文字、证明过程或演算步骤。在试卷上作答无效。