
9、下列说法正确的是( )
A、从外观上可区分硫酸钾和磷矿粉两种肥料
B、等质量的Na2CO3和NaHCO3分别与足量盐酸反应产生等质量的CO2
C、将硝酸铵肥料与生石灰长期堆放在一起
 D、反应3CO + Fe2O3
2Fe + 3CO2 是置换反应
D、反应3CO + Fe2O3
2Fe + 3CO2 是置换反应
8、下列离子组能在PH=1的无色溶液中大量共存的是( )
A、NO3- Fe3+ Na+ OH-
B、K+ SO42- Na+ NO3-
C、Cl- K+ SO42+ Ba2+
D、Ca2+ Cl- CO32- Na+
7、水是地球上最普遍、最常见的物质之一,人类的日常生活离不开水。下列有关水的说法正确的是( )
A、水蒸发后,化学性质发生了变化
B、水电解生成氢气和氧气,说明水中含有氢分子和氧分子
C、冰块与水混合得到混合物
D、明矾可用于净水
6、二百多年前,法国化学家拉瓦锡通过实验得出氧气约占空气总体积的1/5,有关氧气的叙述正确的是( )
A、具有可燃性 B、铁丝在氧气中燃烧火星四射
C、硫在氧气中燃烧生成三氧化硫 D、木炭在氧气中燃烧生成刺激性气味的气体
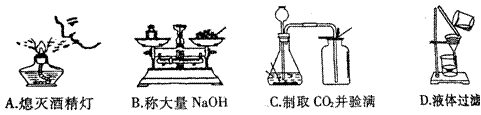
5、下列实验操作中正确的是( )
4、2010年5月23日下午,汶川水磨镇大槽村山上,11岁男孩罗豪等在一个废弃作坊内被烧伤,生命垂危。同学们应吸取教训、珍爱生命,懂得一些燃烧与爆炸的基本常识。下列图标与燃烧和爆炸无关的是( )
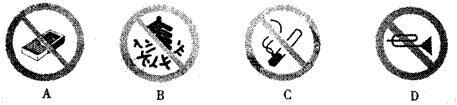
3、化学不仅要研究自然界已经存在的物质及其变化,还要根据需要研究和创造新物质。下列物质属于天然有机高分子材料的是( )
A、棉花 B、葡萄糖 C、涤纶 D、聚乙烯
2、下列物质属于纯净物的是( )
A、生铁 B、矿泉水 C、碘酒 D、硝酸钾晶体
1、下列变化不属于化学变化的是( )
A、鲜奶制酸奶 B、糯米酿甜酒
C、铁杵磨成针 D、氢氧化钠溶液中加少量胆矾
(15)(本小题共13分)
已知函数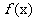
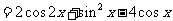 。
。
(Ⅰ)求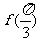 的值;
的值;
(Ⅱ)求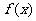 的最大值和最小值。
的最大值和最小值。
15
(I)
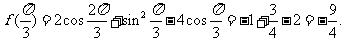
(2)
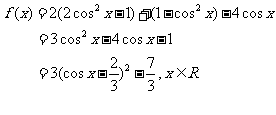
因为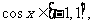 所以当
所以当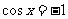 时,
时,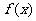 取最大值6;当
取最大值6;当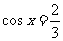 时,取最小值
时,取最小值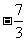 。
。
(16)(本小题共14分)
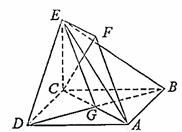 如图,正方形ABCD和四边形ACEF所在的平面互相垂直,CE⊥AC,EF∥AC,AB=
如图,正方形ABCD和四边形ACEF所在的平面互相垂直,CE⊥AC,EF∥AC,AB= ,CE=EF=1.
,CE=EF=1.
(Ⅰ)求证:AF∥平面BDE;
(Ⅱ)求证:CF⊥平面BDE;
(Ⅲ)求二面角A-BE-D的大小。
16 证明:(I)设AC与BD交于点G,因为EF∥AG,且EF=1,AG=
证明:(I)设AC与BD交于点G,因为EF∥AG,且EF=1,AG=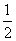 AC=1,所以四边形AGEF为平行四边形。所以AF∥EG。因为EG
AC=1,所以四边形AGEF为平行四边形。所以AF∥EG。因为EG P平面BDE,AF
P平面BDE,AF 平面BDE,所以AF∥平面BDE。
平面BDE,所以AF∥平面BDE。
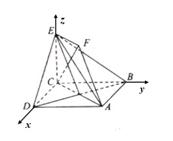 (II)因为正方形ABCD和四边形ACEF所在的平面互相垂直,且CE⊥AC,所以CE⊥AC,所以CE⊥平面ABCD。如图,以C为原点,建立空间直角坐标系C-xyz。则C(0, 0, 0),A(
(II)因为正方形ABCD和四边形ACEF所在的平面互相垂直,且CE⊥AC,所以CE⊥AC,所以CE⊥平面ABCD。如图,以C为原点,建立空间直角坐标系C-xyz。则C(0, 0, 0),A( ,
, ,0),D(
,0),D( ,0, 0),E(0, 0, 1),F(
,0, 0),E(0, 0, 1),F(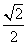 ,
,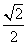 ,1)。所以
,1)。所以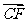 =(
=(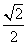 ,
,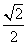 ,1),
,1),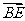 =(0,-
=(0,- ,1),
,1),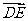 =(-
=(- ,0,1)。所以
,0,1)。所以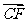 ·
·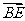 =
0-1+1=0,
=
0-1+1=0,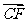 ·
·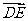 =-1+0+1=0。所以CF⊥BE,CF⊥DE,所以CF⊥平面BDE
=-1+0+1=0。所以CF⊥BE,CF⊥DE,所以CF⊥平面BDE
(III)由(II)知,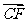 =(
=(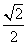 ,
,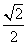 ,1),是平面BDE的一个法向量,设平面ABE的法向量
,1),是平面BDE的一个法向量,设平面ABE的法向量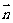 =(x,y,z),则
=(x,y,z),则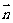 ·
·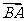 =0,
=0,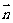 ·
·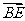 =0。
=0。
即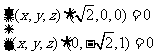
所以x=0,且z= y。令y=1,则z=
y。令y=1,则z= 。所以n=(
。所以n=(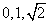 ),从而cos(
),从而cos(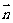 ,
,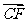 )=
)=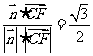
因为二面角A-BE-D为锐角,所以二面角A-BE-D为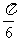 。
。
(17)(本小题共13分)
某同学参加3门课程的考试。假设该同学第一门课程取得优秀成绩的概率为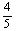 ,第二、第三门课程取得优秀成绩的概率分别为
,第二、第三门课程取得优秀成绩的概率分别为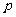 ,
,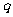 (
(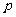 >
>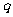 ),且不同课程是否取得优秀成绩相互独立。记ξ为该生取得优秀成绩的课程数,其分布列为
),且不同课程是否取得优秀成绩相互独立。记ξ为该生取得优秀成绩的课程数,其分布列为
|
ξ |
0 |
1 |
2 |
3 |
|
P |
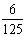 |
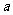 |
b |
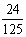 |
(Ⅰ)求该生至少有1门课程取得优秀成绩的概率;
(Ⅱ)求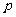 ,
,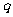 的值;
的值;
(Ⅲ)求数学期望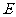 ξ。
ξ。
17
解:事件A,表示“该生第i门课程取得优异成绩”,i=1,2,3。由题意可知
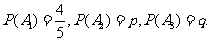
(I)由于事件“该生至少有一门课程取得优异成绩”与事件“ ”是对立的,所以该生至少有一门课程取得优秀成绩的概率是
”是对立的,所以该生至少有一门课程取得优秀成绩的概率是

(II)由题意可知,
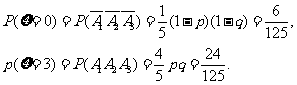
整理得pq=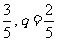 。
。
(III)由题意知,
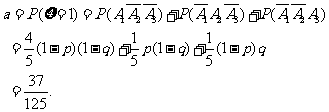
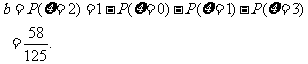
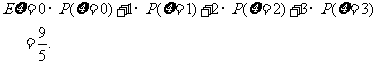
(18)(本小题共13分)
已知函数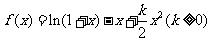
(Ⅰ)当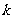 =2时,求曲线
=2时,求曲线 =
=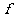 (
(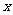 )在点(1,
)在点(1,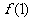 )处的切线方程;
)处的切线方程;
(Ⅱ)求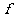 (
(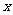 )的单调区间。
)的单调区间。
18
解:(I)当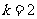 时,
时, 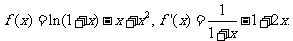
由于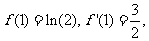 所以曲线
所以曲线 处的切线方程为
处的切线方程为
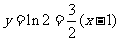 。即
。即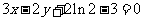
(II)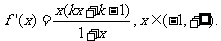
当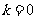 时,
时,
因此在区间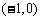 上,
上,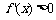 ;在区间
;在区间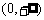 上,
上,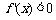 ;
;
所以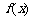 的单调递增区间为
的单调递增区间为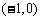 ,单调递减区间为
,单调递减区间为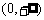 ;
;
当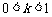 时,
时,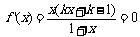 ,得
,得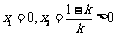 ;
;
因此,在区间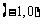 和
和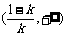 上,
上,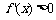 ;在区间
;在区间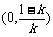 上,
上,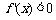 ;
;
即函数 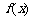 的单调递增区间为
的单调递增区间为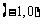 和
和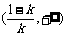 ,单调递减区间为
,单调递减区间为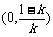 ;
;
当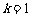 时,
时,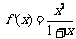 .
.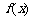 的递增区间为
的递增区间为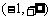
当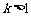 时,由
时,由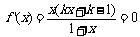 ,得
,得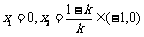 ;
;
因此,在区间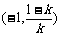 和
和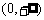 上,
上,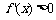 ,在区间
,在区间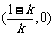 上,
上,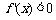 ;
;
即函数 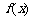 的单调递增区间为
的单调递增区间为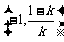 和
和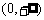 ,单调递减区间为
,单调递减区间为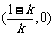 。
。
(19)(本小题共14分)
在平面直角坐标系xOy中,点B与点A(-1,1)关于原点O对称,P是动点,且直线AP与BP的斜率之积等于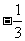 .
.
(Ⅰ)求动点P的轨迹方程;
(Ⅱ)设直线AP和BP分别与直线x=3交于点M,N,问:是否存在点P使得△PAB与△PMN的面积相等?若存在,求出点P的坐标;若不存在,说明理由。
19,
解:(1)因点B与(-1,1)关于原点对称,得B点坐标为(1,-1)。
设P点坐标为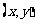 ,则
,则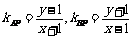 ,由题意得
,由题意得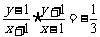 ,
,
化简得: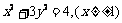 。
。
即P点轨迹为: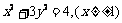
(2)因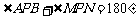 ,可得
,可得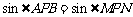 ,
,
又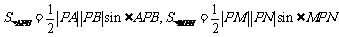 ,
,
若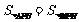 ,则有
,则有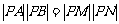 , 即
, 即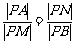
设P点坐标为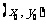 ,则有:
,则有: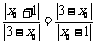
解得: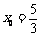 ,又因
,又因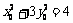 ,解得
,解得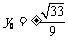 。
。
故存在点P使得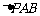 与
与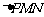 的面积相等,此时P点坐标为
的面积相等,此时P点坐标为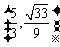 或
或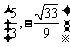
(20)(本小题共13分)
已知集合 对于
对于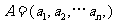 ,
,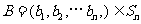 ,定义A与B的差为
,定义A与B的差为
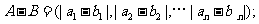
A与B之间的距离为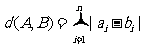
(Ⅰ)证明: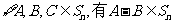 ,且
,且 ;
;
(Ⅱ)证明: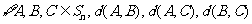 三个数中至少有一个是偶数
三个数中至少有一个是偶数
(Ⅲ) 设P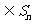 ,P中有m(m≥2)个元素,记P中所有两元素间距离的平均值为
,P中有m(m≥2)个元素,记P中所有两元素间距离的平均值为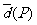 .
.
证明: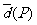 ≤
≤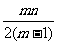 .
.
20,
[分析]:这道题目的难点主要出现在读题上,这里简要分析一下。
题目所给的条件其实包含两个定义,第一个是关于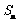 的,其实
的,其实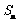 中的元素就是一个n维的坐标,其中每个坐标值都是0或者1, 也可以这样理解,就是一个n位数字的数组,每个数字都只能是0和1, 第二个定义叫距离,距离定义在两者之间,如果直观理解就是看两个数组有多少位不同,因为只有0和1才能产生一个单位的距离,因此这个大题最核心的就是处理数组上的每一位数,然后将处理的结果综合起来,就能看到整体的性质了。
中的元素就是一个n维的坐标,其中每个坐标值都是0或者1, 也可以这样理解,就是一个n位数字的数组,每个数字都只能是0和1, 第二个定义叫距离,距离定义在两者之间,如果直观理解就是看两个数组有多少位不同,因为只有0和1才能产生一个单位的距离,因此这个大题最核心的就是处理数组上的每一位数,然后将处理的结果综合起来,就能看到整体的性质了。
第一问,因为每个数位上都是0或者1,取差的绝对值仍然是0或者1,符合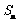 的要求。然后是减去C的数位,不管减去的是0还是1, 每一个a和每一个b都是同时减去的,因此不影响他们原先的差。
的要求。然后是减去C的数位,不管减去的是0还是1, 每一个a和每一个b都是同时减去的,因此不影响他们原先的差。
第二问,先比较A和B有几个不同(因为距离就是不同的有几个),然后比较A和C有几个不同,这两者重复的(就是某一位上A和B不同,A和C不同,那么这一位上B和C就相同)去掉两次(因为在前两次比较中各计算了一次),剩下的就是B和C的不同数目,很容易得到这样的关系式: ,从而三者不可能同为奇数。
,从而三者不可能同为奇数。
第三问,首先理解P中会出现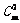 个距离,所以平均距离就是距离总和再除以
个距离,所以平均距离就是距离总和再除以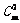 ,而距离的总和仍然可以分解到每个数位上,第一位一共产生了多少个不同,第二位一共产生了多少个不同,如此下去,直到第n位。然后思考,第一位一共m个数,只有0和1会产生一个单位距离,因此只要分开0和1的数目即可,等算出来
,而距离的总和仍然可以分解到每个数位上,第一位一共产生了多少个不同,第二位一共产生了多少个不同,如此下去,直到第n位。然后思考,第一位一共m个数,只有0和1会产生一个单位距离,因此只要分开0和1的数目即可,等算出来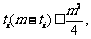 一切就水到渠成了。
一切就水到渠成了。
此外,这个问题需要注意一下数学语言的书写规范。
解:(1)设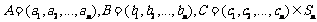
因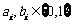 ,故
,故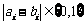 ,
,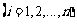
即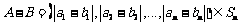
又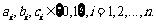
当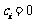 时,有
时,有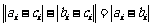 ;
;
当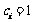 时,有
时,有
故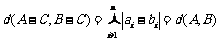
(2)设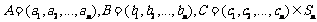
记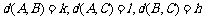
记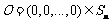 ,由第一问可知:
,由第一问可知:
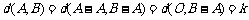
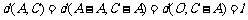
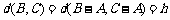
即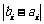 中1的个数为k,
中1的个数为k,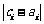 中1的个数为l,
中1的个数为l,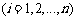
设t是使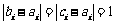 成立的i的个数,则有
成立的i的个数,则有 ,
,
由此可知,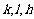 不可能全为奇数,即
不可能全为奇数,即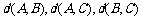 三个数中至少有一个是偶数。
三个数中至少有一个是偶数。
(3)显然P中会产生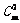 个距离,也就是说
个距离,也就是说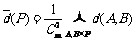 ,其中
,其中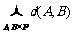 表示P中每两个元素距离的总和。
表示P中每两个元素距离的总和。
分别考察第i个位置,不妨设P中第i个位置一共出现了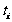 个1, 那么自然有
个1, 那么自然有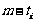 个0,因此在这个位置上所产生的距离总和为
个0,因此在这个位置上所产生的距离总和为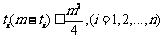 ,
,
那么n个位置的总和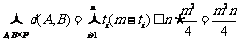
即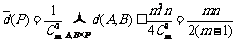
下面就一些具体问题来阐述一下解题思路,希望可以指点今后高三学生的一些复习方向。
选择题,第5题,考察知识点:极坐标系,在这个问题的设置上,命题人很巧妙地加入了一个乘积为0的现象,这违背了不少考生在之前的模拟考试中对于极坐标题的认识,认为就是简简单单的坐标转化,这一设置虽未增加多少难度,但构思仍然值得称赞。
选择题,第6题,考察知识点:常用逻辑,向量。借助函数的背景,把几个小知识点灵活地放在一起,若略有粗心便可能失分。
选择题,第7题,考察知识点:线性规划,指数函数。同样是求参数范围,这道题却能突破常规,最大值是3容易想,所有的a大于1却需要学生敏锐的观察力。
选择题,第8题,考察知识点:立体几何。四个运动的点会让考生感觉不太舒服,而几何的美妙之处很大程度上就在于如何从运动中寻找不变,这也是一向北京市命题风格,09年的选择题最后一题也体现了这个风格。
填空题,第14题,一个正方形的滚动虽然是新背景,但也不是第一次在考试中见到,但是这样的滚动方式还是会让不少学生感觉陌生,如何迅速地考察运动状态的每一次变化,就成为了解决这个问题的关键。
解答题整体难度梯度较好,第15题直接考察三角函数虽然有些出人意外,但题目本身中规中矩,跟平时三角函数的练习并没有太大区别,立体几何,概率,导数三道大题也依然维持常态,与我们平时在课堂上讲解的东西保持一致。值得说的是最后两道大题。
19题为解析几何大题,第二问很多考生反映说计算量很大,的确,如果按照一般的计算交点然后计算距离的方式去求三角形面积,计算量的确不小,但是这样做的同学大多数都是拿到题目,未详细思考直接动笔运算,事实上,如果认真考察两个三角形之间的关系,便可以发现这道题目并不需要过于复杂的运算,我后面给出的解法口算即可完成。
最后一题的立意继承了07年的压轴题立意,在离散情况下处理集合的新背景规则,带有一些组合技巧。考生的瓶颈在于读题上,大多数同学读到复杂的符号和定义的时候便头晕眼花,这说明了许多考生对于数学语言的理解层面尚浅,不能将抽象的符号语言转化为直观的认识,北京近年来的压轴题风格多为此类,下一届的高三应该在这方面多下功夫。
2010年普通高等学校招生全国统一考试
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com