
8.已知直线ax+by+1=0中的a,,b是取自集合{-3,-2,-1,0,1,2}中的2个不同的元素,并且直线的倾斜角大于60°,那么符合这些直线的条数共有 ( )
A.8条 B.11条 C.13条 D.16条
7.一生产过程有4道工序,每道工序需要安排一人照看.现从甲、乙、丙等6名工人中安排4人分别照看一道工序,第一道工序只能从甲、乙两工人中安排1人,第四道工序只能从甲、 丙两工人中安排1人,则不同的安排方案共有( )
丙两工人中安排1人,则不同的安排方案共有( )
A.24种 B.36种 C.48种 D.72种
6.(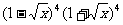 的展开式中
的展开式中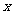 的系数是( )
的系数是( )
A. B.
B. C.3 D.
C.3 D. 4
4
5.随机变量X的概率分布规律为P(X=n)=(n=1,2,3,4),其中a是常数,则
 P(<X<)的值为( )
P(<X<)的值为( )
A. B. C. D.
4.高三(一)班需要安排毕业晚会的4个音乐节目,2个舞蹈节目和一个曲艺节目的演出顺序,要求两个舞蹈节目不连排。则不同的排法种数是( )
A.1800 B. 5040 C.4320 D. 3600
3.12名同学合影,站成前排4人后排8人,现摄影师要从后排8人中抽2人调整到前排,若其他人的相对 顺序不变,则不同调整方法的总数是 (
顺序不变,则不同调整方法的总数是 (  )
)
A. 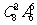 B.
B.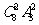 C.
C.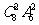 D.
D.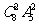

2. 的展开式中含x偶数次幂的项的系数和是( )
的展开式中含x偶数次幂的项的系数和是( )
A.
1024
B. -1023
C. -1024  D.
-2048
D.
-2048
1.C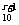 +C
+C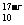 的不
的不 同值有( )个w.w.w o.m
同值有( )个w.w.w o.m
A. 1
B. 2
C.
3
 D. 4
D. 4
4.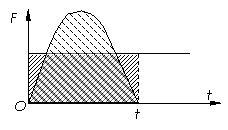 在F-t图中的冲量:
在F-t图中的冲量:
F-t图上的“面积”表示冲量的大小。
[例11]如果物体所受空气阻力与速度成正比,当以速度v1竖直上抛后,又以速度v2返回出发点。这个过程共用了多少时间?
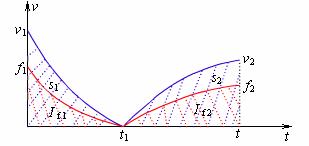
解析:如图所示,作出上升阶段和下降阶段的v-t图线(图中蓝色线所示),则图线下方的“面积”表示位移大小,即s1=s2=h,由于阻力与速度大小成正比,在图中作出f-t图线(图中红色线所示),则图线下方的面积一定相等,而此“面积”表示上升阶段和下降阶段阻力的冲量,即有If 1=If 2,对全过程由动量定理可得mgt=m(v1+v2),解得t=(v1+v2)/g
点评:该题是利用物理图象解题的范例,运用物理图象解题形象直观,可以使解题过程大大简化。
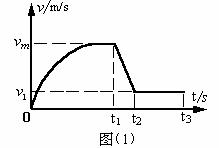
[例12]跳伞运动员从2000m高处跳下,开始下落过程未打开降落伞,假设初速度为零,所受空气阻力与下落速度大小成正比,最大降落速度为vm=50m/s。运动员降落到离地面s=200m高处才打开降落伞,在1s内速度均匀减小到v1=5.0m/s,然后匀速下落到地面,试求运动员在空中运动的时间。
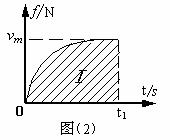
解析:整个过程中,先是变加速运动,接着匀减速,最后匀速运动,作出v-t图线如图(1)所示。由于第一段内作非匀变速直线运动,用常规方法很难求得这1800m位移内的运动时间。考虑动量定理,将第一段的v-t图按比例转化成f-t图,如图(2)所示,则可以巧妙地求得这段时间。
设变加速下落时间为t1,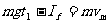

又:mg=kvm,得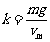 所以:
所以: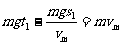

第二段1s内: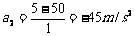
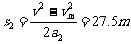
所以第三段时间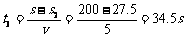
空中的总时间: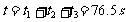
3.动量定理的定量计算
利用动量定理解题,必须按照以下几个步骤进行:
(1)明确研究对象和研究过程。研究对象可以是一个物体,也可以是几个物体组成的质点组。质点组内各物体可以是保持相对静止的,也可以是相对运动的。研究过程既可以是全过程,也可以是全过程中的某一阶段。
(2)进行受力分析。只分析研究对象以外的物体施给研究对象的力。所有外力之和为合外力。研究对象内部的相互作用力(内力)会改变系统内某一物体的动量,但不影响系统的总动量,因此不必分析内力。如果在所选定的研究过程中的不同阶段中物体的受力情况不同,就要分别计算它们的冲量,然后求它们的矢量和。
(3)规定正方向。由于力、冲量、速度、动量都是矢量,在一维的情况下,列式前要先规定一个正方向,和这个方向一致的矢量为正,反之为负。
(4)写出研究对象的初、末动量和合外力的冲量(或各外力在各个阶段的冲量的矢量和)。
(5)根据动量定理列式求解。
[例7]质量为m的小球,从沙坑上方自由下落,经过时间t1到达沙坑表面,又经过时间t2停在沙坑里。求:
(1)沙对小球的平均阻力F;
(2)小球在沙坑里下落过程所受的总冲量I。
 解析:设刚开始下落的位置为A,刚好接触沙的位置为B,在沙中到达的最低点为C。
解析:设刚开始下落的位置为A,刚好接触沙的位置为B,在沙中到达的最低点为C。
(1)在下落的全过程对小球用动量定理:重力作用时间为t1+t2,而阻力作用时间仅为t2,以竖直向下为正方向,有:
mg(t1+t2)-Ft2=0, 解得: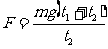
(2)仍然在下落的全过程对小球用动量定理:在t1时间内只有重力的冲量,在t2时间内只有总冲量(已包括重力冲量在内),以竖直向下为正方向,有:
mgt1-I=0,∴I=mgt1
点评:这种题本身并不难,也不复杂,但一定要认真审题。要根据题意所要求的冲量将各个外力灵活组合。若本题目给出小球自由下落的高度,可先把高度转换成时间后再用动量定理。当t1>> t2时,F>>mg。
 [例8] 质量为M的汽车带着质量为m的拖车在平直公路上以加速度a匀加速前进,当速度为v0时拖车突然与汽车脱钩,到拖车停下瞬间司机才发现。若汽车的牵引力一直未变,车与路面的动摩擦因数为μ,那么拖车刚停下时,汽车的瞬时速度是多大?
[例8] 质量为M的汽车带着质量为m的拖车在平直公路上以加速度a匀加速前进,当速度为v0时拖车突然与汽车脱钩,到拖车停下瞬间司机才发现。若汽车的牵引力一直未变,车与路面的动摩擦因数为μ,那么拖车刚停下时,汽车的瞬时速度是多大?
解析:以汽车和拖车系统为研究对象,全过程系统受的合外力始终为 ,该过程经历时间为v0/μg,末状态拖车的动量为零。全过程对系统用动量定理可得:
,该过程经历时间为v0/μg,末状态拖车的动量为零。全过程对系统用动量定理可得:
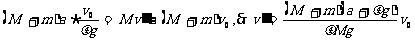
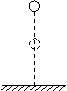 点评:这种方法只能用在拖车停下之前。因为拖车停下后,系统受的合外力中少了拖车受到的摩擦力,因此合外力大小不再是
点评:这种方法只能用在拖车停下之前。因为拖车停下后,系统受的合外力中少了拖车受到的摩擦力,因此合外力大小不再是 。
。
[例9] 质量为m=1kg的小球由高h1=0.45m处自由下落,落到水平地面后,反跳的最大高度为h2=0.2m,从小球下落到反跳到最高点经历的时间为Δt=0.6s,取g=10m/s2。求:小球撞击地面过程中,球对地面的平均压力的大小F。
解析:以小球为研究对象,从开始下落到反跳到最高点的全过程动量变化为零,根据下降、上升高度可知其中下落、上升分别用时t1=0.3s和t2=0.2s,因此与地面作用的时间必为t3=0.1s。由动量定理得:mgΔt-Ft3=0 ,F=60N
[例10] 一个质量为m=2kg的物体,在F1=8N的水平推力作用下,从静止开始沿水平面运动了t1=5s,然后推力减小为F2=5N,方向不变,物体又运动了t2=4s后撤去外力,物体再经 过t3=6s停下来。试求物体在水平面上所受的摩擦力。
解析:
解法l 取物体为研究对象,它的运动可明显分为三个过程。设第一、二两过程末的速度分别为v1和v2。,物体所受摩擦力为f,规定推力的方向为正方向。根据动量定理对三个过程分别有:
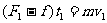

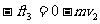
联立上述三式得 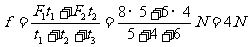
解法2 规定推力的方向为正方向,在物体运动的整个过程中,物体的初动量p1=0,末动量p2=0。据动量定理有
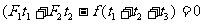
即: 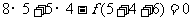
解得 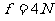
点评:遇到涉及力、时间和速度变化的问题时,运用动量定理解答往往比运用牛顿运动定律及运动学规律求解简便。由解法2可知,合理选取研究过程,能简化解题步骤,提高解题速度。本题也可以用牛顿运动定律求解。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com