15.①，③，⑤

[解析]令，排除②②；由，命题①正确；

，命题③正确；，命题⑤正确。

[方法总结]

14.

[解析]该地拥有3套或3套以上住房的家庭可以估计有：户，

所以所占比例的合理估计是.

[方法总结]本题分层抽样问题，首先根据拥有3套或3套以上住房的家庭所占的比例，得出100 000户，居民中拥有3套或3套以上住房的户数，它除以100 000得到的值，为该地拥有3套或3套以上住房的家庭所占比例的合理估计.

(15)若，则下列不等式对一切满足条件的恒成立的是　　　 (写出所有正确命题的编号)．

①；　　　　 ②；　　 ③ ；

　④；　　 ⑤

13.12

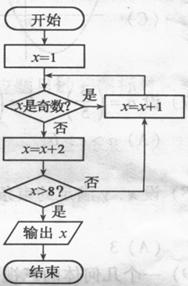
[解析]程序运行如下:,输出12。

[规律总结]这类问题，通常由开始一步一步运行，根据判断条件，要么几步后就会输出结果，要么就会出现规律，如周期性，等差或等比数列型.

(14)某地有居民100 000户，其中普通家庭99 000户,高收入家庭1 000户．从普通家庭中以简单随机抽样方式抽取990户，从高收入家庭中以简单随机抽样方式抽取l00户进行调查，发现共有120户家庭拥有3套或3套以上住房，其中普通家庭50户，高收人家庭70户．依据这些数据并结合所掌握的统计知识，你认为该地拥有3套或3套以上住房的家庭所占比例的合理估计是　　　 .

12.

[解析]抛物线，所以，所以焦点.

[误区警示]本题考查抛物线的交点.部分学生因不会求，或求出后，误认为焦点，还有没有弄清楚焦点位置，从而得出错误结论.

(13)如图所示，程序框图(算法流程图)的输出值x=　　　

(11)命题“存在，使得”的

否定是　　　

11.对任意，都有.

[解析]特称命题的否定时全称命题，“存在”对应“任意”.

[误区警示]这类问题的常见错误是没有把全称量词改为存在量词，或者对于“>”的否定用“<”了.这里就有注意量词的否定形式.如“都是”的否定是“不都是”，而不是“都不是”.

(12)抛物线的焦点坐标是　　　

10.C

[解析]正方形四个顶点可以确定6条直线，甲乙各自任选一条共有36个基本事件。两条直线相互垂直的情况有5种(4组邻边和对角线)包括10个基本事件，所以概率等于.

[方法技巧]对于几何中的概率问题，关键是正确作出几何图形，分类得出基本事件数，然后得所求事件保护的基本事件数，进而利用概率公式求概率.

第Ⅱ卷(非选择题共100分)

9.B

[解析]该几何体由两个长方体组合而成，其表面积等于下面长方体的全面积加上面长方体的4个侧面积之和。

.

[方法技巧]把三视图转化为直观图是解决问题的关键.又三视图很容易知道是两个长方体的组合体，画出直观图，得出各个棱的长度.把几何体的表面积转化为下面长方体的全面积加上面长方体的4个侧面积之和。

(10)甲从正方形四个顶点中任意选择两个顶点连成直线，乙从该正方形四个顶点中任意选择两个顶点连成直线，则所得的两条直线相互垂直的概率是

(A)　　　　 (A)　　　　　　 (A)　　　　　 (A)

8.C

[解析]不等式表示的区域是一个三角形，3个顶点是，目标函数在取最大值6。

[规律总结]线性规划问题首先作出可行域，若为封闭区域(即几条直线围成的区域)则区域端点的值是目标函数取得最大或最小值，求出直线交点坐标代入目标函数即可求出最大值.

(9)一个几何体的三视图如图，该几何体的表面积是

(A)372　　　　　　　　　 (B)360　

(C)292　　　　　　　　　 (D)280

7.A

[解析]在时是增函数，所以，在时是减函数，所以。

[方法总结]根据幂函数与指数函数的单调性直接可以判断出来.

(8)设x,y满足约束条件则目标函数z=x+y的最大值是

(A)3　　　　　　　　 (B) 4　　　　　　　　 (C) 6　　　　　　　 (D)8

6.D

[解析]当时，、同号，(C)(D)两图中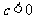，故，选项(D)符合

[方法技巧]根据二次函数图像开口向上或向下，分或两种情况分类考虑.另外还要注意c值是抛物线与y轴交点的纵坐标，还要注意对称轴的位置或定点坐标的位置等.

(7)设，则a，b，c的大小关系是

(A)a＞c＞b　　　　 (B)a＞b＞c　　　　 (C)c＞a＞b　　 (D)b＞c＞a