
20.[命题意图]本题考查导数的运算,利用导数研究函数的单调性与极值的方法,考查综合应用数学知识解决问题的能力.
[解题指导](1)对函数 求导,对导函数用辅助角公式变形,利用导数等于0得极值点,通过列表的方法考查极值点的两侧导数的正负,判断区间的单调性,求极值.
求导,对导函数用辅助角公式变形,利用导数等于0得极值点,通过列表的方法考查极值点的两侧导数的正负,判断区间的单调性,求极值.

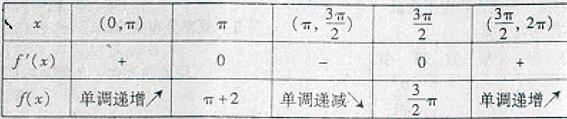

[思维总结]对于函数解答题,一般情况下都是利用导数来研究单调性或极值,利用导数为0得可能的极值点,通过列表得每个区间导数的正负判断函数的单调性,进而得出极值点.
(21)(本小题满分13分)
 设
设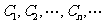 是坐标平面上的一列圆,它们的圆心都在
是坐标平面上的一列圆,它们的圆心都在 轴的正半轴上,且都与直线
轴的正半轴上,且都与直线 相切,对每一个正整数
相切,对每一个正整数 ,圆
,圆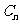 都与圆
都与圆 相互外切,以
相互外切,以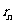 表示
表示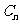 的半径,已知
的半径,已知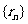 为递增数列.
为递增数列.
(Ⅰ)证明: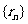 为等比数列;
为等比数列;
(Ⅱ)设 ,求数列
,求数列 的前
的前 项和.
项和.
20.(本小题满分12分)
设函数 ,
, ,求函数
,求函数 的单调区间与极值。
的单调区间与极值。
19.[命题意图]本题考查空间线面平行、线面垂直、面面垂直的判断与证明,考查体积的计算等基础知识,同时考查空间想象能力、推理论证能力和运算能力.
[解题指导](1)设底面对角线交点为G,则可以通过证明EG∥FH,得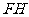 ∥平面
∥平面 ;(2)利用线线、线面的平行与垂直关系,证明FH⊥平面ABCD,得FH⊥BC,FH⊥AC,进而得EG⊥AC,
;(2)利用线线、线面的平行与垂直关系,证明FH⊥平面ABCD,得FH⊥BC,FH⊥AC,进而得EG⊥AC, 平面
平面 ;(3)证明BF⊥平面CDEF,得BF为四面体B-DEF的高,进而求体积.
;(3)证明BF⊥平面CDEF,得BF为四面体B-DEF的高,进而求体积.

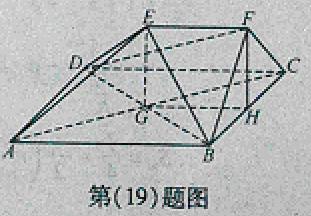

[规律总结]本题是典型的空间几何问题,图形不是规则的空间几何体,所求的结论是线面平行与垂直以及体积,考查平行关系的判断与性质.解决这类问题,通常利用线线平行证明线面平行,利用线线垂直证明线面垂直,通过求高和底面积求四面体体积.
19.(本小题满分13分)
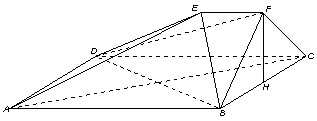 如图,在多面体ABCDEF中,四边形ABCD是正方形,AB=2EF=2,EF∥AB,EF⊥FB,∠BFC=90°,BF=FC,H为BC的中点,
如图,在多面体ABCDEF中,四边形ABCD是正方形,AB=2EF=2,EF∥AB,EF⊥FB,∠BFC=90°,BF=FC,H为BC的中点,
(Ⅰ)求证:FH∥平面EDB;
(Ⅱ)求证:AC⊥平面EDB;
(Ⅲ)求四面体B—DEF的体积;
18.[命题意图]本题考查频数,频率及频率分布直方图,考查运用统计知识解决简单实际问题的能力,数据处理能力和运用意识.
[解题指导](1)首先根据题目中的数据完成频率分布表,作出频率分布直方图,根据污染指数,确定空气质量为优、良、轻微污染、轻度污染的天数。

(Ⅲ)答对下述两条中的一条即可:
(1)
该市一个月中空气污染指数有2天处于优的水平,占当月天数的 ,有26天处于良的水平,占当月天数的
,有26天处于良的水平,占当月天数的 ,处于优或良的天数共有28天,占当月天数的
,处于优或良的天数共有28天,占当月天数的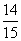 。说明该市空气质量基本良好。
。说明该市空气质量基本良好。
(2) 轻微污染有2天,占当月天数的 。污染指数在80以上的接近轻微污染的天数有15天,加上处于轻微污染的天数,共有17天,占当月天数的
。污染指数在80以上的接近轻微污染的天数有15天,加上处于轻微污染的天数,共有17天,占当月天数的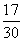 ,超过50%,说明该市空气质量有待进一步改善。
,超过50%,说明该市空气质量有待进一步改善。
[规律总结]在频率分布表中,频数的和等于样本容量,频率的和等于1,每一小组的频率等于这一组的频数除以样本容量.频率分布直方图中,小矩形的高等于每一组的频率/组距,它们与频数成正比,小矩形的面积等于这一组的频率.对于开放性问题的回答,要选择适当的数据特征进行考察,根据数据特征分析得出实际问题的结论.
18、(本小题满分13分)
某市2010年4月1日—4月30日对空气污染指数的监测数据如下(主要污染物为可吸入颗粒物):
61,76,70,56,81,91,92,91,75,81,88,67,101,103,95,91,
77,86,81,83,82,82,64,79,86,85,75,71,49,45,
(Ⅰ) 完成频率分布表;
(Ⅱ)作出频率分布直方图;
(Ⅲ)根据国家标准,污染指数在0~50之间时,空气质量为优:在51~100之间时,为良;在101~150之间时,为轻微污染;在151~200之间时,为轻度污染。
请你依据所给数据和上述标准,对该市的空气质量给出一个简短评价.
17.[命题意图]本题考查椭圆的定义及标准方程,椭圆的简单几何性质,直线的点斜式方程与一般方程,点到直线的距离公式等基础知识;考查解析几何的基本思想、综合运算能力.
[解题指导](1)设椭圆方程为 ,把点
,把点 代入椭圆方程,把离心率
代入椭圆方程,把离心率 用
用 表示,再根据
表示,再根据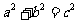 ,求出
,求出 ,得椭圆方程;(2)可以设直线l上任一点坐标为
,得椭圆方程;(2)可以设直线l上任一点坐标为 ,根据角平分线上的点到角两边距离相等得
,根据角平分线上的点到角两边距离相等得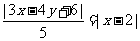 .
.
解:(Ⅰ)设椭圆E的方程为


[规律总结]对于椭圆解答题,一般都是设椭圆方程为 ,根据题目满足的条件求出
,根据题目满足的条件求出 ,得椭圆方程,这一问通常比较简单;(2)对于角平分线问题,利用角平分线的几何意义,即角平分线上的点到角两边距离相等得方程.
,得椭圆方程,这一问通常比较简单;(2)对于角平分线问题,利用角平分线的几何意义,即角平分线上的点到角两边距离相等得方程.
17、(本小题满分12分)
椭圆 经过点
经过点 ,对称轴为坐标轴,
,对称轴为坐标轴,
焦点 在
在 轴上,离心率
轴上,离心率 。
。
(Ⅰ)求椭圆 的方程;
的方程;
(Ⅱ)求 的角平分线所在直线的方程。
的角平分线所在直线的方程。
16.[命题意图]本题考查同角三角函数的基本关系,三角形面积公式,向量的数量积,利用余弦定理解三角形以及运算求解能力.
[解题指导](1)根据同角三角函数关系,由 得
得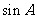 的值,再根据
的值,再根据 面积公式得
面积公式得 ;直接求数量积
;直接求数量积 .由余弦定理
.由余弦定理 ,代入已知条件
,代入已知条件 ,及
,及 求a的值.
求a的值.
解:由 ,得
,得 .
.
又 ,∴
,∴ .
.
(Ⅰ)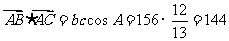 .
.
(Ⅱ)
 ,
,
∴ .
.
 [规律总结]根据本题所给的条件及所要求的结论可知,需求
[规律总结]根据本题所给的条件及所要求的结论可知,需求 的值,考虑已知
的值,考虑已知 的面积是30,
的面积是30, ,所以先求
,所以先求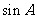 的值,然后根据三角形面积公式得
的值,然后根据三角形面积公式得 的值.第二问中求a的值,根据第一问中的结论可知,直接利用余弦定理即可.
的值.第二问中求a的值,根据第一问中的结论可知,直接利用余弦定理即可.
16、(本小题满分12分)
 的面积是30,内角
的面积是30,内角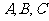 所对边长分别为
所对边长分别为 ,
, 。
。
(Ⅰ)求 ;
;
(Ⅱ)若 ,求
,求 的值。
的值。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com