
4.该国1975-2005年期间 ,人口增长的特点是 ( )
A.总量有波动,但变化不大 B.总量上升,增长速度减缓
C.经历了慢-快-慢的过程 D.总量上升,增长速度加快
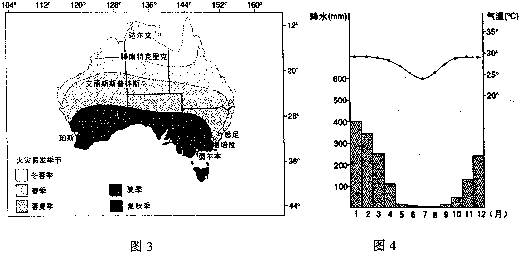
图3表示澳大利亚不同地区最容易发生火灾的季节,图4是达尔文的气候统计图。读图回答5、6题。
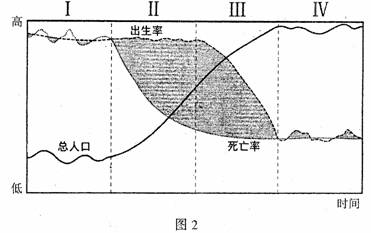
3.该国处于图2中的 ( )
A.阶段I B.阶段II C.阶段III D.阶段IV
2.该科学家在考察地区发现多座火山,这些火山是
由于 ( )
A.非洲板块不断张裂而形成的
B.亚欧板块与非洲板块碰撞形成的
C.南极洲板块与美洲板块碰撞形成的
D.太平洋板块与美洲板块碰撞形成的
表1是某国出生率、死亡率的变化情况,图2是人口增长模式图。回答第3、4题。
|
|
1975年 |
1985年 |
1995年 |
2005年 |
|
出生率(%) |
4.4 |
4.3 |
4.3 |
4.3 |
|
死亡率(%) |
2.0 |
1.7 |
1.6 |
1.4 |
 本大题共35小题,每小题4分,共140分。在每小题列出的四个选项中,选出最符合题目要求的一项。
本大题共35小题,每小题4分,共140分。在每小题列出的四个选项中,选出最符合题目要求的一项。
图1是某科学家在野外考察时,手持式GPS屏幕上
所显示的信息。据此回答1、2题。
1.科学家所考察地区可能位于 ( )
A.欧洲阿尔卑斯山脉
B.非洲撒哈拉沙漠
C.北美洲西部山地
D.南美洲亚马孙平原
20.(本小题满分14分)
已知函数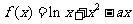 .
.
(Ⅰ)若函数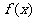 在其定义域上为增函数,求
在其定义域上为增函数,求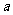 的取值范围;
的取值范围;
(Ⅱ)设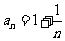 (
(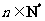 ),求证:
),求证:
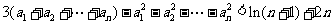 .
.
(考生务必将答案答在答题卡上,在试卷上作答无效)
北京市东城区2009-2010学年度第二学期综合练习(二)
19.(本小题满分13分)
已知椭圆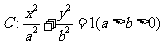 的短轴长为
的短轴长为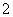 ,且与抛物线
,且与抛物线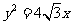 有共同的焦点,椭圆
有共同的焦点,椭圆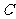 的左顶点为A,右顶点为
的左顶点为A,右顶点为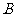 ,点
,点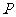 是椭圆
是椭圆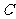 上位于
上位于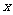 轴上方的动点,直线
轴上方的动点,直线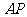 ,
, 与直线
与直线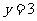 分别交于
分别交于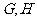 两点.
两点.
(I)求椭圆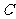 的方程;
的方程;
(Ⅱ)求线段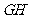 的长度的最小值;
的长度的最小值;
(Ⅲ)在线段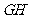 的长度取得最小值时,椭圆
的长度取得最小值时,椭圆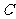 上是否存在一点
上是否存在一点 ,使得
,使得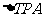 的面积为
的面积为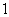 ,若存在求出点
,若存在求出点 的坐标,若不存在,说明理由.
的坐标,若不存在,说明理由.
18.(本小题满分13分)
已知等比数列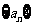 的公比
的公比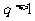 ,
, 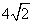 是
是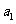 和
和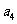 的一个等比中项,
的一个等比中项,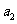 和
和 的等差中项为
的等差中项为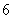 ,若数列
,若数列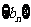 满足
满足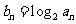 (
(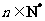 ).
).
(Ⅰ)求数列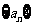 的通项公式;
的通项公式;
(Ⅱ)求数列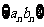 的前
的前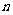 项和
项和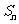 .
.
17.(本小题满分14分)
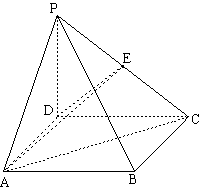
如图,四棱锥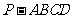 中,
中,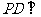 平面
平面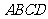 ,底面
,底面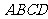 为矩形,
为矩形,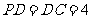 ,
,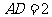 ,
,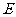 为
为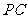 的中点.
的中点.
(Ⅰ)求证: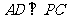 ;
;
(Ⅱ)求三棱锥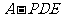 的体积;
的体积;
(Ⅲ) 边上是否存在一点
边上是否存在一点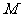 ,使得
,使得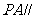 平面
平面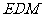 ,若存在,求出
,若存在,求出 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.
16.(本小题满分13分)
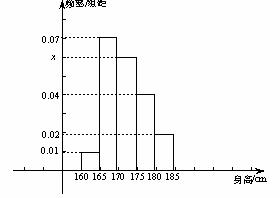
随机抽取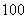 名学生,测得他们的身高(单位:
名学生,测得他们的身高(单位: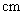 ),按照区间
),按照区间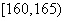 ,
,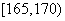 ,
,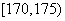 ,
,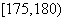 ,
,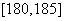 分组,得到样本身高的频率分布直方图(如图).
分组,得到样本身高的频率分布直方图(如图).
(Ⅰ)求频率分布直方图中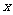 的值及身高在
的值及身高在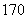
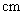 以上的学生人数;
以上的学生人数;
(Ⅱ)将身高在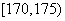 ,
,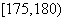 ,
,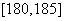 区间内的学生依次记为
区间内的学生依次记为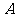 ,
,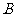 ,
,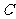 三个组,用分层抽样的方法从三个组中抽取
三个组,用分层抽样的方法从三个组中抽取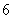 人,求从这三个组分别抽取的学生人数;
人,求从这三个组分别抽取的学生人数;
(Ⅲ)在(Ⅱ)的条件下,要从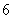 名学生中抽取
名学生中抽取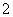 人,用列举法计算
人,用列举法计算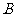 组中至少有
组中至少有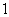 人被抽中的概率.
人被抽中的概率.
15. (本小题满分13分)
在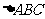 中,角
中,角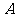 ,
,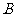 ,
,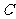 所对的边分别为
所对的边分别为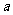 ,
,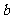 ,
,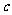 ,且
,且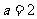 ,
,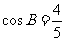 .
.
(Ⅰ)若 ,求
,求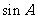 的值;
的值;
(Ⅱ)若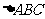 的面积
的面积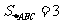 ,求
,求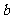 ,
,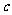 的值21.世纪教
的值21.世纪教
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com