22．　 如图，已知双曲线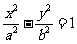(b>a>O)且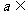[1，2]，它的左、右焦点分别为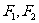，左、右顶点分别为A、B．过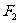作圆的切线，切点为T，交双曲线于P,Q两点.

(1)求证：直线PQ与双曲线的一条渐近线垂直；

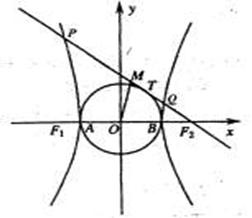(2)若M为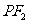的中点，0为坐标原点，∣OM∣-∣MT∣=1，∣PQ∣=∣AB∣，求实数的取值范围．

21．设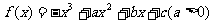，在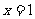处取得极大值，且存在斜率为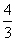的切线。

　 (1)求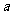的取值范围；

　 (2)若函数在区间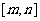上单调递增，求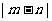的取值范围；

　 (3)是否存在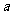的取值使得对于任意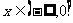，都有。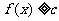

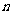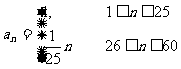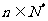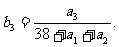20．某商店投入38万元经销某种纪念品，经销时间共60天，为了获得更多的利润，商店将每天获得的利润投入到次日的经营中，市场调研表明，该商店在经销这一产品期间第天的利润(单位：万元，)，记第n天的利润率，例如湖北

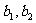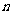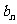　 (1)求的值；湖北　 (2)求第天的利润率；湖北

　 (3)该商店在经销此纪念品期间，哪一天的利润率最大？并求该天的利润率。

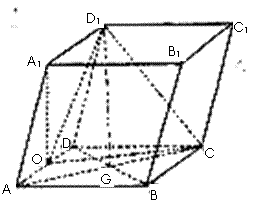
19、如图，平行六面体ABCD-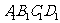中，底面ABCD是边长为2的菱形，∠BAD=，

　 　其中AC与BD交于点G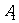，点在面ABCD上的射影0恰好为线段AD的中点。

(I)求点G到平面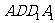距离；

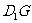(Ⅱ)若与平面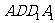所成角的正弦值为，

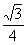　　　　 求二面角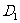-OC-D的大小．

18、为提高某篮球运动员的投篮水平，教练对其平时训练的表现作以详细的数据记录：每

次投中记l分，投不中记-1分，统计平时的数据得该运动员每次投篮命中的概率为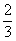，若在某场训练中，该运动员前n次投篮所得总分司为，且每次投篮是否命中相互之间没有影响．

(I)求该篮球运动员前三次投篮所得总分为1的概率；

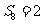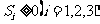(Ⅱ)求出现且的概率。

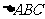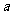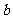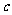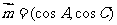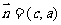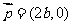17、设的三内角A、B、C所对边的长分别为、、，平面向量，，，且。

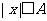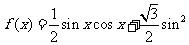
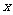(1)求角A的大小；(2)当时，求函数的值域。

13、　　　　　　 　　　14、　　　　　　 　　15、　　　　　　　 　　16、　　　　　　

16、已知函数y＝f(x)是R上的偶函数，对于x∈R都有f(x－6)＝f(x)+f(3)成立，且f(0)＝－2，当x₁,x₂∈[0,3]，且x₁≠x₂时，都有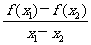>0．则给出下列命题：①f(2010)＝－2；②函数y＝f(x)图象的一条对称轴为x＝－6；③函数y＝f(x)在[－9，－6]上为增函数；④方程f(x)＝0在[－9，9]上有4个根．其中所有正确命题的序号是__________。

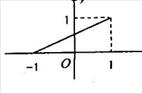
15、函数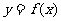的定义域为[-1,1]，图象如图所示，其反函数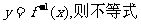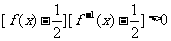的解集为　　　 　

14、已知函数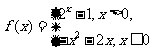 若函数g(x)=f(x)-m有3个零点，则实数m

的取值范围