
13、设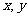 满足约束条件
满足约束条件 ,若目标函数
,若目标函数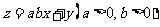 的最大值为8,则
的最大值为8,则 的最小值为________。
的最小值为________。
[答案]4
[解析]不等式表示的区域是一个四边形,4个顶点是
 ,易见目标函数在
,易见目标函数在 取最大值8,
取最大值8,
所以 ,所以
,所以 ,在
,在 时是等号成立。所以
时是等号成立。所以 的最小值为4.
的最小值为4.
 [规律总结]线性规划问题首先作出可行域,若为封闭区域(即几条直线围成的区域)则区域端点的值是目标函数取得最大或最小值,求出直线交点坐标代入得
[规律总结]线性规划问题首先作出可行域,若为封闭区域(即几条直线围成的区域)则区域端点的值是目标函数取得最大或最小值,求出直线交点坐标代入得 ,要想求
,要想求 的最小值,显然要利用基本不等式.
的最小值,显然要利用基本不等式.
12、 展开式中,
展开式中, 的系数等于________。
的系数等于________。
[答案]15
[解析]
11、命题“对任何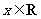 ,
, ”的否定是________。
”的否定是________。
[答案]
[解析]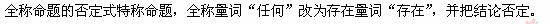
10.D
[分析]取等比数列 ,令
,令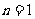 得
得 代入验算,只有
代入验算,只有 选项D满足。
选项D满足。
[方法技巧]对于含有较多字母的客观题,可以取满足条件的数字代替字母,代入验证,若能排除3个选项,剩下唯一正确的就一定正确;若不能完全排除,可以取其他数字验证继续排除.本题也可以首项、公比即项数n表示代入验证得结论.
第Ⅱ卷(非选择题,共90分)
10、设 是任意等比数列,它的前
是任意等比数列,它的前 项和,前
项和,前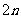 项和与前
项和与前 项和分别为
项和分别为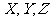 ,则下列等式中恒成立的是
,则下列等式中恒成立的是
A、 B、
B、
C、 D、
D、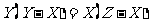
9.D
[解析]画出图形,设动点A与 轴正方向夹角为
轴正方向夹角为 ,则
,则 时
时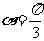 ,每秒钟旋转
,每秒钟旋转 ,在
,在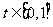 上
上 ,在
,在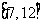 上
上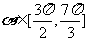 ,动点
,动点 的纵坐标
的纵坐标 关于
关于 都是单调递增的。
都是单调递增的。
[方法技巧]由动点 在圆
在圆 上绕坐标原点沿逆时针方向匀速旋转,可知与三角函数的定义类似,由12秒旋转一周能求每秒钟所转的弧度,画出单位圆,很容易看出,当t在
上绕坐标原点沿逆时针方向匀速旋转,可知与三角函数的定义类似,由12秒旋转一周能求每秒钟所转的弧度,画出单位圆,很容易看出,当t在 变化时,点
变化时,点 的纵坐标
的纵坐标 关于
关于 (单位:秒)的函数的单调性的变化,从而得单调递增区间.
(单位:秒)的函数的单调性的变化,从而得单调递增区间.
9、动点 在圆
在圆 上绕坐标原点沿逆时针方向匀速旋转,12秒旋转一周。已知时间
上绕坐标原点沿逆时针方向匀速旋转,12秒旋转一周。已知时间 时,点
时,点 的坐标是
的坐标是 ,则当
,则当 时,动点
时,动点 的纵坐标
的纵坐标 关于
关于 (单位:秒)的函数的单调递增区间是
(单位:秒)的函数的单调递增区间是
A、 B、
B、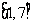 C、
C、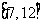 D、
D、 和
和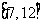
8.C
[解析]该几何体由两个长方体组合而成,其表面积等于下面长方体的全面积加上面长方体的4个侧面积之 和。
和。 .
.
[方法技巧]把三视图转化为直观图是解决问题的关键.又三视图很容易知道是两个长方体的组合体,画出直观图,得出各个 棱的长度.把几何体的表面积转化为下面长方体的全面积加上面长方体的4个侧面积之和。
棱的长度.把几何体的表面积转化为下面长方体的全面积加上面长方体的4个侧面积之和。
8、一个几何体的三视图如图,该几何体的表面积为
A、280 B、292 C、360 D、372
7.B
[解析]化曲线 的参数方程为普通方程:
的参数方程为普通方程: ,圆心
,圆心 到直线
到直线 的距离
的距离 ,直线和圆相交,过圆心和
,直线和圆相交,过圆心和 平行的直线和圆的2个交点符合要求,又
平行的直线和圆的2个交点符合要求,又 ,在直线
,在直线 的另外一侧没有圆上的点符合要求,所以选B.
的另外一侧没有圆上的点符合要求,所以选B.
[方法总结]解决这类问题首先把曲线 的参数方程为普通方程,然后利用圆心到直线的距离判断直线与圆的位置关系,这就是曲线
的参数方程为普通方程,然后利用圆心到直线的距离判断直线与圆的位置关系,这就是曲线 上到直线
上到直线 距离为
距离为 ,然后再判断知
,然后再判断知 ,进而得出结论.
,进而得出结论.

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com