
9.[答案]C
[解析]曲线方程可化简为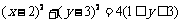 ,即表示圆心为(2,3)半径为2的半圆,依据数形结合,当直线
,即表示圆心为(2,3)半径为2的半圆,依据数形结合,当直线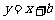 与此半圆相切时须满足圆心(2,3)到直线y=x+b距离等于2,解得
与此半圆相切时须满足圆心(2,3)到直线y=x+b距离等于2,解得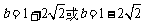 ,因为是下半圆故可得
,因为是下半圆故可得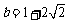 (舍),当直线过(0,3)时,解得b=3,故
(舍),当直线过(0,3)时,解得b=3,故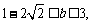 所以C正确.
所以C正确.
8.[答案]B
[解析]分类讨论:若有2人从事司机工作,则方案有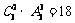 ;若有1人从事司机工作,则方案有
;若有1人从事司机工作,则方案有 种,所以共有18+108=126种,故B正确
种,所以共有18+108=126种,故B正确
7.[答案]C
[解析]依题意分析可知,图形中内切圆半径分别为:
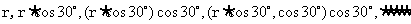 即
即
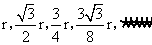 则面积依次为:
则面积依次为: 所以
所以
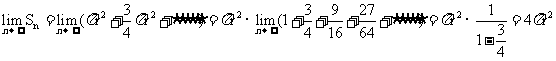 故C正确.
故C正确.
6.[答案]B
[解析]依题意可知,在随机抽样中,首次抽到003号,以后每隔12个号抽到一个人,则分别是003、015、027、039 构成以3为首项,12为公差的等差数列,故可分别求出在001到300中有25人,在301至495号中共有17人,则496到600中有8人, 所以B正确。
构成以3为首项,12为公差的等差数列,故可分别求出在001到300中有25人,在301至495号中共有17人,则496到600中有8人, 所以B正确。
5.[答案]B
[解析]由题目条件可知,M为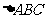 的重心,连接
的重心,连接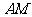 并延长交
并延长交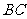 于
于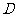 ,则
,则 ①, 因为
①, 因为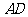 为中线
为中线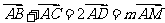 ,
,
即 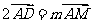 ②, 联立①②可得
②, 联立①②可得 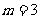 ,故
,故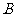 正确。
正确。
4.[答案]C
[解析]用间接法考虑,事件A、B一个都不发生的概率为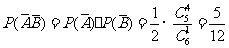
则所求概率 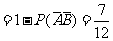 , 故C 正确。
, 故C 正确。
3.[答案]D
[解析]根据正弦定理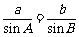 可得
可得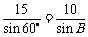 解得
解得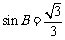 ,又因为
,又因为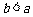 ,则
,则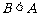 ,故B为锐角,所以
,故B为锐角,所以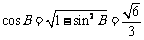 ,故D正确.
,故D正确.
2.[答案]A
[解析]画出椭圆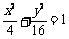 和指数函数
和指数函数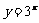 图象,可知其有两个不同交点,记为A1、A2,则
图象,可知其有两个不同交点,记为A1、A2,则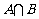 的子集应为
的子集应为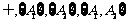 共四种,故选A.
共四种,故选A.
1.[答案]D
[解析]观察图形可知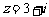 ,则
,则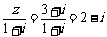 ,即对应点H(2,-1),故D正确.
,即对应点H(2,-1),故D正确.
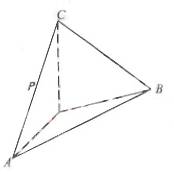
18. (本小题满分12分)
如图, 在四面体ABOC中, 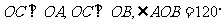 , 且
, 且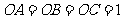
(Ⅰ)设为 为
为 的中点, 证明: 在
的中点, 证明: 在 上存在一点
上存在一点 ,使
,使 ,并计算
,并计算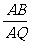 的值;
的值;
 (Ⅱ)求二面角
(Ⅱ)求二面角 的平面角的余弦值。
的平面角的余弦值。
19(本小题满分12分)
已知一条曲线C在y轴右边,C上每一点到点F(1,0)的距离减去它到y轴距离的差都是1.
(Ⅰ)求曲线C的方程;
(Ⅱ)是否存在正数m,对于过点M(m,0)且与曲线C有两个交点A,B的任一直线,都有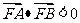 ?若存在,求出m的取值范围;若不存在,请说明理由。
?若存在,求出m的取值范围;若不存在,请说明理由。

(Ⅲ) 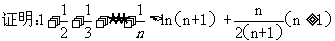
2010年高考试题--数学理
(湖北卷)答案与解析
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com