3、．如图所示一列横波在t₁和t₂时刻的波形分别如图中的实线和虚线所示，已知波的传播速度是2.0m/s。

①若t₂－t₁＝1.5s，则波是向右传播的

②若t₂－t₁＝1.5s，则波是向左传播的

③若t₂－t₁＝2.5s，则t₂时刻质元P向y轴正方向运动

④若t₂－t₁＝2.5s，则t₂时刻质元P向y轴负方向运动

上述结论正确的是　　　　　　　　　　　　　　　　　　　　　　 (　　　　 )

A．①③　　　 B．②③　　　 C．①④　　　 D．②④

答案：A

2、居室装修中经常用到花岗岩、大理石等装饰材料，有些含有铀、钍的岩石会释放出放射性气体氡。人们若经常处于高浓度氡环境中，氡会经呼吸进入人体并停留于呼吸道中进行放射性衰变，放射出α、β、γ射线。这些射线会导致细胞发生癌变，引发肺癌、白血病及呼吸道等方面的疾病。下列说法正确的是　　　　　

A．铀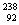U衰变为氡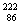Rn要经过4次α衰变和4次β衰变

B．处于激发态的氡原子发出一束蓝光照射到某金属能产生光电效应，若这束蓝光被遮住一半，则不会产生光电效应

C．放射性元素发生β衰变时所释放的电子是原子核内的中子衰变为质子时产生的

D．放射性元素在发生α衰变时2个中子和2个质子结合为一个α粒子，设中子、质子和α粒子的质量分别为m₁、m₂、m₃，则2(m₁+m₂)=m₃

答案：C

1、华裔科学家高锟因发明“光导纤维”而获得诺贝尔奖，高锟的研究为人类进入光纤通讯的新纪元打开了大门。如图所示，a、b两束单色光合在一起同时从光导纤维的左端面垂直射入，其中a单色光先射出右端面，则下列判断正确的是(　　 )。_￥￥

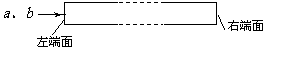A．a光的频率高于b光的频率

B．a光的折射率比b光的折射率大

C．a光在真空中的速度大于b光在真空中的速度

D．a光在真空中的波长大于b光在真空中的波长

答案：D

4.

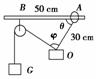
图2－4－13

如图2－4－13所示，在质量为1 kg的重物上系着一条长30 cm的细绳，细绳的另一端连着套在水平棒上可以滑动的圆环，环与棒间的动摩擦因数为0.75，另有一条细绳，其一端跨过定滑轮，定滑轮固定在距离圆环0.5 m的地方．当细绳的端点挂上重物G，而圆环将要滑动时，试问：

(1)长为30 cm的细绳的张力是多少？

(2)圆环将要开始滑动时，重物G的质量是多少？

(3)角φ多大？(环的重力忽略不计)

解析：因为圆环将要开始滑动，所以可以判定本题是在共点力作用下物体的平衡问题．由平衡条件?F_x＝0，?F_y＝0，建立方程有：μF_N－F_Tcos θ＝0，F_N－F_Tsin θ＝0.

所以tan θ＝，θ＝arctan＝arctan.

设想：过O作OA的垂线与杆交于B′点，由AO＝30 cm，tan θ＝得，B′O的长为40 cm.

在直角三角形中，由三角形的边长条件得AB′＝50 cm，但据题设条件AB＝50 cm，故B′点与定滑轮的固定处B点重合，即得φ＝90°.

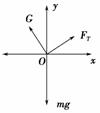
(1)如图所示，选取坐标系，根据平衡条件有：

Gcos θ+F_Tsin θ－mg＝0

F_Tcos θ－Gsin θ＝0.

即　F_T＝8 N.

(2)圆环将要滑动时，得：

m_Gg＝F_Tcot θ，m_G＝0.6 kg.

(3)前已证明φ为直角，故φ＝90°.

答案：(1)8 N　(2)0.6 kg　(3)90°

3.

图2－4－12

如图2－4－12所示，一根弹性细绳原长为l，劲度系数为k，将其一端穿过一个光滑小孔O(其在水平地面上的投影点为O′)，系在一个质量为m的滑块A上，A放在水平地面上．小孔O离绳固定端的竖直距离为l，离水平地面高度为h(h<mg/k)，滑块A与水平地面间的最大静摩擦力为正压力的μ倍．问：

(1)当滑块与O′点距离为r时，弹性细绳对滑块A的拉力为多大？

(2)滑块处于怎样的区域内时可以保持静止状态？

解析：(1)当滑块与O′点的距离为r时，弹性细绳的伸长量为Δx＝ .

由胡克定律知，弹性绳的拉力F＝kΔx＝k

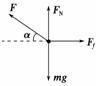
(2)设OA与水平面的夹角为α，分析物体受力如图所示，由平衡条件得：

F_N+Fsin α＝mg

Fcos α＝F_f.

而F＝k，Ff_m＝μF_N

所以有：k·cos α＝F_f≤Ff_m＝μ(mg－Fsin α)＝μ(mg－kh)

其中cos α＝r，故r≤

答案：(1)k

(2)以O′为圆心，以为半径的圆内的任何位置

2.

图2－4－11

表面光滑、半径为R的半球固定在水平地面上，球心O的正上方O′处有一无摩擦的定滑轮，轻质细绳两端各系一个小球挂在定滑轮上，如图2－4－11所示，两小球平衡时，若滑轮两侧细绳的长度分别为L₁＝2.4R和L₂＝2.5R，则这两个小球的质量之比m₁∶m₂为(不计球的大小)(　)

A．24∶1　 　　　　 B．25∶1

C．24∶25　 　　　 D．25∶24

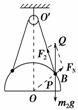
解析：对小球2进行受力分析，如右图所示，显然△O′OP与△PBQ相似．

设OO′＝H，OP＝R，O′P＝L₂，

由相似三角形的性质有m₂g/H＝F_N/R＝F₂/L₂，

则m₂＝F₂H/(gL₂)，同理可得m₁＝F₁H/(gL₁)

而F₁＝F₂，于是m₁/m₂＝L₂/L₁＝25∶24.

答案：D

1.

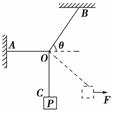
图2－4－10

如图2－4－10所示，用绳OA、OB和OC吊着重物P处于静止状态，其中绳OA水平，绳OB与水平方向成θ角．现用水平向右的力F缓慢地将重物P拉起，用F_A和F_B分别表示绳OA和绳OB的张力，则(　)

A．F_A、F_B、F均增大　 　　　　　　　 B．F_A增大，F_B不变，F增大

C．F_A不变，F_B减小，F增大　 　　　　　 D．F_A增大，F_B减小，F减小

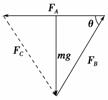
解析：把OA、OB和OC三根绳和重物P看作一个整体，整体受到重力mg，A点的拉力F_A，方向沿着OA绳水平向左，B点的拉力F_B，方向沿着OB绳斜向右上方，水平向右的拉力F而处于平衡状态，有：F_A＝F+F_Bcos θ，F_Bsin θ＝mg，因为θ不变，所以F_B不变．再以O点进行研究，O点受到OA绳的拉力，方向不变，沿着OA绳水平向左，OB绳的拉力，大小和方向都不变，OC绳的拉力，大小和方向都可以变化，O点处于平衡状态，因此这三个力构成一个封闭的矢量三角形(如图)，刚开始F_C由竖直方向逆时针旋转到图中的虚线位置，因此F_A和F_C同时增大，又F_A＝F+F_Bcos θ，F_B不变，所以F增大，所以B正确．

答案：B

12．一辆值勤的警车停在公路边，当警员发现从他旁边以10 m/s的速度匀速行驶的货车严重超载时，决定前去追赶，经过5.5 s后警车发动起来，并以2.5 m/s²的加速度做匀加速运动，但警车的行驶速度必须控制在90 km/h以内．问：

(1)警车在追赶货车的过程中，两车间的最大距离是多少？

(2)警车发动后要多长时间才能追上货车？

解析：(1)警车在追赶货车的过程中，当两车速度相等时．它们间的距离最大，设警车发动后经过t₁时间两车的速度相等．则t₁＝ s＝4 s，x_货＝(5.5+4)×10 m＝95 m，

x_警＝at＝×2.5×4² m＝20 m，所以两车间的最大距离Δx＝x_货－x_警＝75 m.

(2)v₀＝90 km/h＝25 m/s，当警车刚达到最大速度时，运动时间t₂＝ s＝10 s

x_货′＝(5.5+10)×10 m＝155 m，x_警′＝at＝×2.5×10² m＝125 m

因为x_货′＞x_警′，故此时警车尚未赶上货车，且此时两车距离Δx′＝x_货′－x_警′＝30 m

警车达到最大速度后做匀速运动，设再经过Δt时间追赶上货车，则Δt＝＝2 s

所以警车发动后要经过t＝t₂+Δt＝12 s才能追上货车．

答案：(1)75 m　(2)12 s

11.

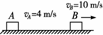
图1－3－24

如图1－3－24所示，A、B两物体相距s＝7 m时，A在水平拉力和摩擦力作用下，正以v_A＝4 m/s的速度向右匀速运动，而物体B此时正以v_B＝10 m/s的初速度向右匀减速运动，加速度a＝－2 m/s²，求A追上B所经历的时间．

解析：物体B减速至静止的时间为t，则－v_B＝at₀，t₀＝ s＝5 s

物体B向前运动的位移x_B＝v_Bt₀＝×10×5 m＝25 m.

又因A物体5 s内前进x_A＝v_At₀＝20 m，显然x_B+7 m＞x_A.

所以A追上B前，物体B已经静止，设A追上B经历的时间为t′，则t′＝＝ s＝8 s.

答案：8 s

10.

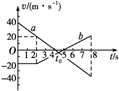
图1－3－23

如图1－3－23所示，a、b分别是甲、乙两辆车从同一地点沿同一直线同时运动的速度图象，由图象可以判断(　)

A．2 s后甲、乙两车的加速度大小相等

B．在0-8 s内两车最远相距148 m

C．两车只有t₀时刻速率相等

D．两车在t＝8 s时相遇

解析：2 s后，|a_甲|＝ m/s²＝10 m/s²，|a_乙|＝ m/s²，故|a_甲|>|a_乙|，A错；t＝2 s时和t＝t₀时，甲、乙速率均相等，故C错；t＝8 s时，甲回到出发点，乙没有回到出发点，故D错；由题干图可知两车在0-8 s内相距最远应在t₀时刻，由a、b两直线可求出t₀＝4.4 s，则两车相距最远距x应为a、b两线和纵轴围成的面积，解得x＝148 m，故B对．

答案：B