
2、(解析者提供答案参考)“好风凭借力,送我上青云”这是宝钗的思想写照,“一年三百六十日,风刀霜剑严相逼”这是黛玉的生活环境,《红楼梦》诗词文质兼美。今天我们将对它进行专题鉴赏,希望同学们积极发言。
[试题分析]1、点明鉴赏《红楼梦》诗词;2、号召学生积极参与;3、尽量使用《红楼梦》中的诗词。
[高考考点]扩展语句
(10年天津卷)
21.某中学研究型学习小组举办《红楼梦》读书交流会。主题是“《红楼梦》诗词鉴赏”。请为主持人写一则开场白。要求:①紧扣主题;②表达得体,富有文采;③不写称呼语、问候语;④不超过60字。(4分)W高考ww.ks资源5u.co网m
[答案示例]1、(标准答案参考)“满纸荒唐言”,“谁解其中味”,绝世奇书《红楼梦》中的诗词也是难得的艺术瑰宝。让我们走进宝山,去欣赏他们的璀璨与绚丽吧。
2、(解析者提供答案参考)月光在竹林中洒下斑斑光点,四周一片寂静。一阵风吹来,传来洗衣归来的少女的喧哗。话音如玉盘落珠般清脆,笑声如银铃摇动般响亮,是这般地无忧无虑。
[试题分析]注意几个要素:竹、浣女归、喧。尽量体现王诗“诗中有画”的意境。
[高考考点]扩展语句
(10年湖北卷)
20.请根据王维的诗句“竹喧归浣女”写一个场景。要求:①想象合理;②语言生动;③不超过50字。(4分)
W高考ww.ks资源5u.co网m
[答案示例]1、(标准答案参考)浣完衣服的少女拎着水桶,踏着月色,从婆娑的竹林间穿过,伴着银铃般的笑声,叽叽喳喳的打闹着归来。
2.常见题型
万有引力定律的应用主要涉及几个方面:
(1)测天体的质量及密度:(万有引力全部提供向心力)
由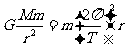 得
得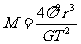
又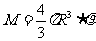 得
得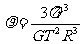
[例1]中子星是恒星演化过程的一种可能结果,它的密度很大。现有一中子星,观测到它的自转周期为T=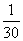 s。问该中子星的最小密度应是多少才能维持该星的稳定,不致因自转而瓦解。计算时星体可视为均匀球体。(引力常数G=6.67
s。问该中子星的最小密度应是多少才能维持该星的稳定,不致因自转而瓦解。计算时星体可视为均匀球体。(引力常数G=6.67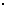 10
10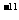 m
m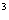 /kg.s
/kg.s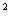 )
)
解析:设想中子星赤道处一小块物质,只有当它受到的万有引力大于或等于它随星体所需的向心力时,中子星才不会瓦解。
设中子星的密度为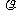 ,质量为M ,半径为R,自转角速度为
,质量为M ,半径为R,自转角速度为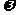 ,位于赤道处的小物块质量为m,则有
,位于赤道处的小物块质量为m,则有 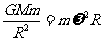
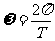
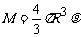
由以上各式得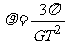 ,代入数据解得:
,代入数据解得: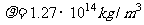 。
。
点评:在应用万有引力定律解题时,经常需要像本题一样先假设某处存在一个物体再分析求解是应用万有引力定律解题惯用的一种方法。
(2)行星表面重力加速度、轨道重力加速度问题:(重力近似等于万有引力)
表面重力加速度: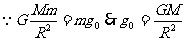
轨道重力加速度: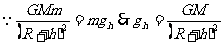
[例2]一卫星绕某行星做匀速圆周运动,已知行星表面的重力加速度为g0,行星的质量M与卫星的质量m之比M/m=81,行星的半径R0与卫星的半径R之比R0/R=3.6,行星与卫星之间的距离r与行星的半径R0之比r/R0=60。设卫星表面的重力加速度为g,则在卫星表面有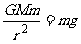 ……
……
经过计算得出:卫星表面的重力加速度为行星表面的重力加速度的1/3600。上述结果是否正确?若正确,列式证明;若有错误,求出正确结果。
解析:题中所列关于g的表达式并不是卫星表面的重力加速度,而是卫星绕行星做匀速圆周运动的向心加速度。正确的解法是
卫星表面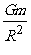 =g 行星表面
=g 行星表面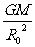 =g0
即
=g0
即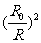
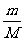 =
=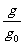
即g =0.16g0。
(3)人造卫星、宇宙速度:
人造卫星分类(略):其中重点了解同步卫星
宇宙速度:(弄清第一宇宙速度与发卫星发射速度的区别)
[例3]我国自行研制的“风云一号”、“风云二号”气象卫星运行的轨道是不同的。“一号”是极地圆形轨道卫星。其轨道平面与赤道平面垂直,周期是12h;“二号”是地球同步卫星。两颗卫星相比 号离地面较高; 号观察范围较大; 号运行速度较大。若某天上午8点“风云一号”正好通过某城市的上空,那么下一次它通过该城市上空的时刻将是 。
解析:根据周期公式T=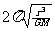 知,高度越大,周期越大,则“风云二号”
气象卫星离地面较高;根据运行轨道的特点知,“风云一号” 观察范围较大;根据运行速度公式V=
知,高度越大,周期越大,则“风云二号”
气象卫星离地面较高;根据运行轨道的特点知,“风云一号” 观察范围较大;根据运行速度公式V=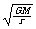 知,高度越小,速度越大,则“风云一号”
运行速度较大,由于“风云一号”卫星的周期是12h,每天能对同一地区进行两次观测,在这种轨道上运动的卫星通过任意纬度的地方时时间保持不变。则下一次它通过该城市上空的时刻将是第二天上午8点。
知,高度越小,速度越大,则“风云一号”
运行速度较大,由于“风云一号”卫星的周期是12h,每天能对同一地区进行两次观测,在这种轨道上运动的卫星通过任意纬度的地方时时间保持不变。则下一次它通过该城市上空的时刻将是第二天上午8点。
[例4]可发射一颗人造卫星,使其圆轨道满足下列条件( )
A、与地球表面上某一纬度线(非赤道)是共面的同心圆
B、与地球表面上某一经度线是共面的同心圆
C、与地球表面上的赤道线是共面同心圆,且卫星相对地面是运动的
D、与地球表面上的赤道线是共面同心圆,且卫星相对地面是静止的
解析:卫星绕地球运动的向心力由万有引力提供,且万有引力始终指向地心,因此卫星的轨道不可能与地球表面上某一纬度线(非赤道)是共面的同心圆,故A是错误的。由于地球在不停的自转,即使是极地卫星的轨道也不可能与任一条经度线是共面的同心圆,故B是错误的。赤道上的卫星除通信卫星采用地球静止轨道外,其它卫星相对地球表面都是运动的,故C、D是正确的。
[例5]侦察卫星在通过地球两极上的圆轨道上运行,它的运行轨道距地面高度为h,要使卫星在一天的时间内将地面上赤道各处在日照条件的情况下全都拍摄下来,卫星在通过赤道上空时,卫星上的摄像机至少应拍摄地面上赤道圆周的弧长是多少?设地球半径为R,地面处的重力加速度为g,地球自转的周期为T。
解析:如果周期是12小时,每天能对同一地区进行两次观测。如果周期是6小时,每天能对同一纬度的地方进行四次观测。如果周期是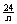 小时,每天能对同一纬度的地方进行n次观测。
小时,每天能对同一纬度的地方进行n次观测。
设上星运行周期为T1,则有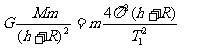
物体处在地面上时有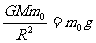 解得:
解得: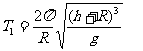
在一天内卫星绕地球转过的圈数为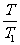 ,即在日照条件下有
,即在日照条件下有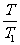 次经过赤道上空,所以每次摄像机拍摄的赤道弧长为
次经过赤道上空,所以每次摄像机拍摄的赤道弧长为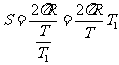 ,将T1结果代入得
,将T1结果代入得 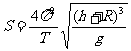
[例6]在地球(看作质量均匀分布的球体)上空有许多同步卫星,下面说法中正确的是( )
A.它们的质量可能不同 B.它们的速度可能不同
C.它们的向心加速度可能不同 D.它们离地心的距离可能不同
解析:同步卫星绕地球近似作匀速圆周运动所需的向心力由同步卫星的地球间的万有引力提供。设地球的质量为M,同步卫星的质量为m,地球半径为R,同步卫星距离地面的高度为h,由F引=F向, G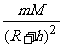 =m
=m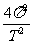 (R+h)得:h=
(R+h)得:h=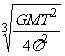 -R,可见同步卫星离地心的距离是一定的。
-R,可见同步卫星离地心的距离是一定的。
由G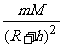 =m
=m 得:v=
得:v=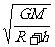 ,所以同步卫星的速度相同。
,所以同步卫星的速度相同。
由G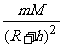 =ma得:a= G
=ma得:a= G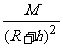 即同步卫星的向心加速度相同。
即同步卫星的向心加速度相同。
由以上各式均可看出地球同步卫星的除质量可以不同外,其它物理量值都应是固定的。所以正确选项为A。
点评:需要特别提出的是:地球同步卫星的有关知识必须引起高度重视,因为在高考试题中多次出现。所谓地球同步卫星,是相对地面静止的且和地球有相同周期、角速度的卫星。其运行轨道与赤道平面重合。
[例7]地球同步卫星到地心的距离r可由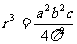 求出,已知式中a的单位是m,b的单位是s,c的单位是m/s2,则:
求出,已知式中a的单位是m,b的单位是s,c的单位是m/s2,则:
A.a是地球半径,b是地球自转的周期,C是地球表面处的重力加速度;
B.a是地球半径。b是同步卫星绕地心运动的周期,C是同步卫星的加速度;
C.a是赤道周长,b是地球自转周期,C是同步卫星的加速度
D.a是地球半径,b是同步卫星绕地心运动的周期,C是地球表面处的重力加速度。
解析:由万有引力定律导出人造地球卫星运转半径的表达式,再将其与题给表达式中各项对比,以明确式中各项的物理意义。AD正确。
[例8]我国自制新型“长征”运载火箭,将模拟载人航天试验飞船“神舟三号”送入预定轨道,飞船绕地球遨游太空t=7天后又顺利返回地面。飞船在运动过程中进行了预定的空间科学实验,获得圆满成功。
①设飞船轨道离地高度为h,地球半径为R,地面重力加速度为g.则“神舟三号”飞船绕地球正常运转多少圈?(用给定字母表示)。
②若h=600 km,R=6400 km,则圈数为多少?
解析:(1)在轨道上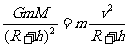 ①
①
v=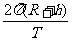 ②
②
在地球表面: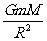 =mg ③
=mg ③
联立①②③式得:T=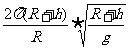
故n=
②代人数据得:n=105圈
(4)双星问题:
[例9]两个星球组成双星,它们在相互之间的万有引力作用下,绕连线上某点做周期相同的匀速圆周运动。现测得两星中心距离为R,其运动周期为T,求两星的总质量。
解析:设两星质量分别为M1和M2,都绕连线上O点作周期为T的圆周运动,星球1和星球2到O的距离分别为l1和l2。由万有引力定律和牛顿第二定律及几何条件可得M1:G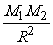 =M1(
=M1(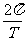 )2 l1 ∴M2=
)2 l1 ∴M2=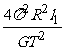
对M2:G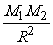 =M2(
=M2(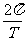 )2 l2 ∴M1=
)2 l2 ∴M1=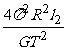
两式相加得M1+M2=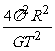 (l1+l2)=
(l1+l2)=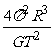 。
。
(5)有关航天问题的分析:
[例10]无人飞船“神州二号”曾在离地高度为H=3. 4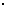 105m的圆轨道上运行了47小时。求在这段时间内它绕行地球多少圈?(地球半径R=6.37
105m的圆轨道上运行了47小时。求在这段时间内它绕行地球多少圈?(地球半径R=6.37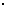 106m,重力加速度g=9.8m/s2)
106m,重力加速度g=9.8m/s2)
解析:用r表示飞船圆轨道半径r=H+ R==6. 71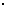 106m
。
106m
。
M表示地球质量,m表示飞船质量,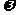 表示飞船绕地球运行的角速度,G表示万有引力常数。由万有引力定律和牛顿定律得
表示飞船绕地球运行的角速度,G表示万有引力常数。由万有引力定律和牛顿定律得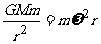
利用G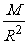 =g得
=g得 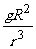 =
=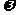 2由于
2由于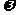 =
=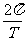 ,T表示周期。解得
,T表示周期。解得
T=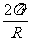
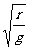 ,又n=
,又n=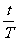 代入数值解得绕行圈数为n=31。
代入数值解得绕行圈数为n=31。
(6)天体问题为背景的信息给予题
近两年,以天体问题为背景的信息给予题在全国各类高考试卷中频频出现,不仅考查学生对知识的掌握,而且考查考生从材料、信息中获取有用信息以及综合能力。这类题目一般由两部分组成:信息给予部分和问题部分。信息给予部分是向学生提供解题信息,包括文字叙述、数据等,内容是物理学研究的概念、定律、规律等,问题部分是围绕信息给予部分来展开,考查学生能否从信息给予部分获得有用信息,以及能否迁移到回答的问题中来。从题目中提炼有效信息是解决此类问题的关键所在。
[例11] 地球质量为M,半径为R,自转角速度为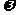 。万有引力恒量为G,如果规定物体在离地球无穷远处势能为0,则质量为m的物体离地心距离为r时,具有的万有引力势能可表示为
。万有引力恒量为G,如果规定物体在离地球无穷远处势能为0,则质量为m的物体离地心距离为r时,具有的万有引力势能可表示为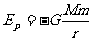 。国际空间站是迄今世界上最大的航天工程,它是在地球大气层上空绕地球飞行的一个巨大人造天体,可供宇航员在其上居住和科学实验。设空间站离地面高度为h,如果杂该空间站上直接发射一颗质量为m的小卫星,使其能到达地球同步卫星轨道并能在轨道上正常运行,由该卫星在离开空间站时必须具有多大的动能?
。国际空间站是迄今世界上最大的航天工程,它是在地球大气层上空绕地球飞行的一个巨大人造天体,可供宇航员在其上居住和科学实验。设空间站离地面高度为h,如果杂该空间站上直接发射一颗质量为m的小卫星,使其能到达地球同步卫星轨道并能在轨道上正常运行,由该卫星在离开空间站时必须具有多大的动能?
解析:由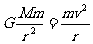 得,卫星在空间站上动能为
得,卫星在空间站上动能为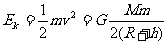
卫星在空间站上的引力势能为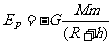
机械能为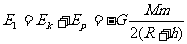
同步卫星在轨道上正常运行时有 故其轨道半径
故其轨道半径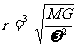
由上式可得同步卫星的机械能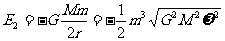
卫星运动过程中机械能守恒,故离开航天飞机的卫星的机械能应为E2设离开航天飞机时卫星的动能为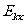 则
则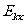 =
=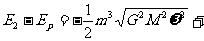
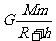
1.解题的相关知识:
(1)在高考试题中,应用万有引力定律解题的知识常集中于两点:一是天体运动的向心力来源于天体之间的万有引力,即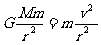 =
=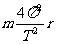
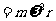 ;二是地球对物体的万有引力近似等于物体的重力,即G
;二是地球对物体的万有引力近似等于物体的重力,即G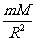 =mg从而得出GM=R
=mg从而得出GM=R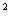 g。
g。
(2)圆周运动的有关公式: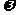 =
=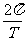 ,v=
,v=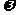 r。
r。
讨论:
①由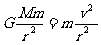 可得:
可得: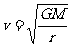 r越大,v越小。
r越大,v越小。
②由 可得:
可得: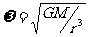 r越大,ω越小。
r越大,ω越小。
③由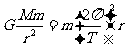 可得:
可得: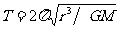 r越大,T越大。
r越大,T越大。
④由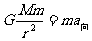 可得:
可得: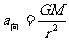 r越大,a向越小。
r越大,a向越小。
点评:需要说明的是,万有引力定律中两个物体的距离,对于相距很远因而可以看作质点的物体就是指两质点的距离;对于未特别说明的天体,都可认为是均匀球体,则指的是两个球心的距离。人造卫星及天体的运动都近似为匀速圆周运动。
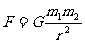
适用于两个质点或均匀球体;r为两质点或球心间的距离;G为万有引力恒量(1798年由英国物理学家卡文迪许利用扭秤装置测出)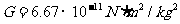
25.如图9,在Rt△ABC中,∠ACB=90°.半径为1的圆A与边AB相交于点D,与边AC相交于点E,连结DE并延长,与线段BC的延长线交于点P.
(1)当∠B=30°时,连结AP,若△AEP与△BDP相似,求CE的长;
(2)若CE=2,BD=BC,求∠BPD的正切值;
(3)若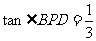 ,设CE=x,△ABC的周长为y,求y关于x的函数关系式.
,设CE=x,△ABC的周长为y,求y关于x的函数关系式.
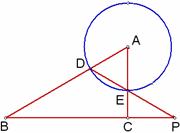
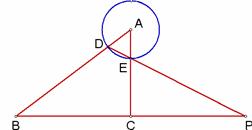
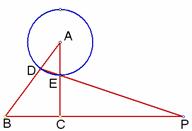
图9 图10(备用) 图11(备用)
(1)解:∵∠B=30°∠ACB=90°∴∠BAC=60°
∵AD=AE ∴∠AED=60°=∠CEP
∴∠EPC=30°
∴三角形BDP为等腰三角形
∵△AEP与△BDP相似
∴∠EAP=∠EPA=∠DBP=∠DPB=30°
∴AE=EP=1
∴在RT△ECP中,EC=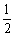 EP=
EP=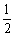
(2)过点D作DQ⊥AC于点Q,且设AQ=a,BD=x
∵AE=1,EC=2
∴QC=3-a
∵∠ACB=90°
∴△ADQ与△ABC相似
∴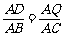
即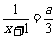 ,∴
,∴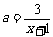
∵在RT△ADQ中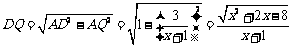
∵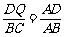
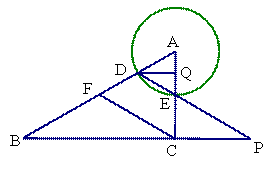 ∴
∴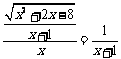
解之得x=4,即BC=4
过点C作CF//DP
∴△ADE与△AFC相似,
∴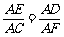 ,即AF=AC,即DF=EC=2,
,即AF=AC,即DF=EC=2,
∴BF=DF=2
∵△BFC与△BDP相似
∴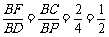 ,即:BC=CP=4
,即:BC=CP=4
∴tan∠BPD=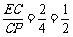
(3)过D点作DQ⊥AC于点Q,则△DQE与△PCE相似,设AQ=a,则QE=1-a
∴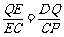 且
且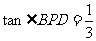
∴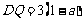
∵在Rt△ADQ中,据勾股定理得: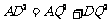
即: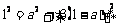 ,解之得
,解之得
∵△ADQ与△ABC相似
∴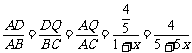
∴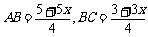
∴三角形ABC的周长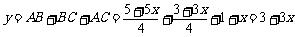
即: ,其中x>0
,其中x>0
24.如图8,已知平面直角坐标系xOy,抛物线y=-x2+bx+c过点A(4,0)、B(1,3) .
(1)求该抛物线的表达式,并写出该抛物线的对称轴和顶点坐标;
(2)记该抛物线的对称轴为直线l,设抛物线上的点P(m,n)在第四象限,点P关于直线l的对称点为E,点E关于y轴的对称点为F,若四边形OAPF的面积为20,求m、n的值.
 (1)解:将A(4,0)、B(1,3)两点坐标代入抛物线的方程得:
(1)解:将A(4,0)、B(1,3)两点坐标代入抛物线的方程得:
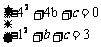
解之得:b=4,c=0
所以抛物线的表达式为: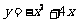
将抛物线的表达式配方得: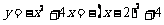
所以对称轴为x=2,顶点坐标为(2,4)
(2)点p(m,n)关于直线x=2的对称点坐标为点E(4-m,n),则点E关于y轴对称点为点F坐标为(4-m,-n),
则四边形OAPF可以分为:三角形OFA与三角形OAP,则
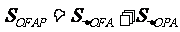 =
= 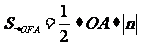 +
+ 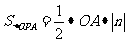 =
= 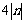 =20
=20
所以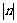 =5,因为点P为第四象限的点,所以n<0,所以n= -5
=5,因为点P为第四象限的点,所以n<0,所以n= -5
代入抛物线方程得m=5
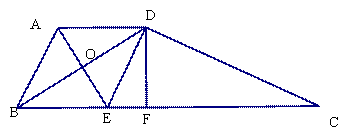
23.已知梯形ABCD中,AD//BC,AB=AD(如图7所示),∠BAD的平分线AE交BC于点E,连结DE.
(1)在图7中,用尺规作∠BAD的平分线AE(保留作图痕迹,不写作法),并证明四边形ABED是菱形;
(2)∠ABC=60°,EC=2BE,求证:ED⊥DC.
(1)解:分别以点B、D为圆心,以大于AB的长度为半径,分别作弧,且两弧交于一点P,则连接AP,即AP即为∠BAD的平分线,且AP交BC于点E,
∵AB=AD,∴△ABO≌△AOD ∴BO=OD
∵AD//BC, ∴∠OBE=∠ODA, ∠OAD=OEB
∴△BOE≌△DOA
∴BE=AD(平行且相等)
∴四边形ABDE为平行四边形,另AB=AD,
∴四边形ADBE为菱形
(2)设DE=2a,则CE=4a,过点D作DF⊥BC
∵∠ABC=60°,∴∠DEF=60°, ∴∠EDF=30°, ∴EF=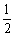 DE=a,则DF=
DE=a,则DF=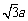 ,CF=CE-EF=4a-a=3a,
,CF=CE-EF=4a-a=3a,
 ∴
∴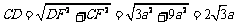
∴DE=2a,EC=4a,CD=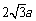 ,构成一组勾股数,
,构成一组勾股数,
∴△EDC为直角三角形,则ED⊥DC
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com