
5. 当呼吸底物不是糖时,有氧呼吸消耗的O2和产生的CO2的体积并不相等。利用如图所示装置两套,设为甲、乙,测定单位质量小麦种子呼吸时CO2释放量与O2消耗量的比值,下列构思可以达到实验目的的是
当呼吸底物不是糖时,有氧呼吸消耗的O2和产生的CO2的体积并不相等。利用如图所示装置两套,设为甲、乙,测定单位质量小麦种子呼吸时CO2释放量与O2消耗量的比值,下列构思可以达到实验目的的是
A.甲装置烧杯中盛放清水,在光照下测定O2释放量,乙装置
在黑暗下测定CO2释放量
B.甲装置烧杯中盛放清水,测定CO2释放量,乙装置换成CO2
吸收剂测定O2消耗量
C.甲装置烧杯中盛放清水,测定气体体积变化量,乙装置换成CO2吸收剂,测定O2消耗量
D.甲装置烧杯中盛放CO2缓冲剂(可吸收和放出CO2),测定氧气消耗量,乙装置放死亡种子作对照
4.取染色体DNA被32P标记的蛙(正常体细胞有26条染色体)的精子与未被标记的卵细胞受精。不考虑染色体变异,下列关于该受精卵及其分裂所产生后代细胞的说法正确的是
A.第二次卵裂结束及原肠胚时,胚体中最多分别有4个和26个细胞带放射性
B.因为在分裂过程中可能发生交叉互换,原肠胚时期带放射性的细胞数无法确定
C.取胚体的细胞制片观察,每个细胞内都可以看到染色体
D.分裂时细胞质遗传物质随机分配,是生物体形成各种不同细胞和组织的主要原因
3.萝卜和甘蓝均为二倍体,利用萝卜和甘蓝作为材料经以下不同处理后得到的植株可育的组合是

 高☆考♂资♀源?网 ☆
高☆考♂资♀源?网 ☆
①萝卜×甘蓝→F1植株
②萝卜×甘蓝→F1经秋水仙素处理加倍植株
③萝卜经秋水仙素处理加倍植株×甘蓝→F1植株④萝卜与甘蓝经体细胞杂交得到的杂种植株
A.①③ B.②③ C.②④ D.③④
2.下列关于黄色短杆菌的叙述,不正确的是
A.黄色短杆菌用于赖氨酸生产时,不能合成高丝氨酸脱氢酶的理想菌株是诱变育种的成果
B.黄色短杆菌在大量合成谷氨酸时,培养基中碳源与氮源的比为3∶1,此时菌体种群
处于稳定期
C.由培养基的成分和发酵条件的控制可知,黄色短杆菌是异养需氧型,在自然界属于分解者
D.黄色短杆菌的性状主要由拟核DNA中的基因决定,其基因结构的特点是编码区是连续的,而黄色短杆菌质粒中的基因结构不具有此特点
1.多倍体是指具有3套或3套以上完整染色体组的生物体,下列有关多倍体形成途径的相关叙述中,错误的是
A.通过基因工程技术可获得高产、稳产和具有优良品质的多倍体农作物
B.生殖细胞减数分裂不正常,使染色体不减半,形成2n配子,这样的配子经受精作用可形成多倍体植株
C.同种或异种植物的原生质体融合成为杂种细胞,杂种细胞形成愈伤组织、进一步分化形成多倍体植株
D.合子或分生组织细胞内的染色体加倍形成多倍体细胞,能够发育成多倍体植株
22.(本小题满分14分)已知f(x)=ax3+bx2+cx+d是定义在R上的函数,其图象交x轴于A,B,C,三点,若点B的坐标为(2,0),且f(x)在[-1,0]和[4,5]上有相同的单调性,在[0,2]和[4,5]上有相反的单调性.
(1)求c的值;
(2)在函数f(x)的图象上是否存在一点M(x0,y0),使得f(x)在点M处的切线斜率为3b?若存在,求出点M的坐标;若不存在,说明理由;
(3)求|AC|的取值范围.
21.
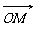
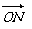 (本小题满分12分) 在平面直角坐标系中,O为坐标原点,已知两点M (1,-3)、N(5,1),若点C满足 =t +(1-t) (t∈R),点C的轨迹与抛物线:y2=4x交于A、B两点。
(本小题满分12分) 在平面直角坐标系中,O为坐标原点,已知两点M (1,-3)、N(5,1),若点C满足 =t +(1-t) (t∈R),点C的轨迹与抛物线:y2=4x交于A、B两点。
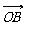
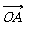 (1)求证: ⊥ ;
(1)求证: ⊥ ;
(2)在x轴上是否存在一点P (m,0),使得过点P任作抛物线的一条弦,并以该弦为直径的圆都过原点.若存在,请求出 m的值及圆心的轨迹方程;若不存在,请说明理由.
20.(本小题满分12分)已知数列{an}的前n项和S n,且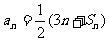 对一切正整数n恒成立.
对一切正整数n恒成立.
(1)证明数列{an+3}为等比数列;
(2)数列{an}是否存在三项构成等差数列?若存在,求出一组;若不存在,请说明理由.
19.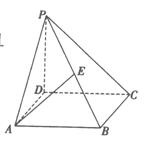 (本小题满分12分) 如图,在四棱维P-ABCD中,底面ABCD为正方形,PD⊥平面ABCD,且PD=AB=a,E是PB的中点.
(本小题满分12分) 如图,在四棱维P-ABCD中,底面ABCD为正方形,PD⊥平面ABCD,且PD=AB=a,E是PB的中点.
(1)求异面直线PD与AE所成角的大小;
(2)在平面PAD内求一点F,使得EF⊥平面PBC;
(3)在(2)的条件下,求二面角F-PC-E的大小.
18.(本小题满分12分) 甲、乙、丙三人分别独立解一道数学题,已知甲做对这道题的概率是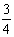 ,甲、丙两人都做错的概率是
,甲、丙两人都做错的概率是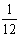 ,乙、丙两人都做对的概率是
,乙、丙两人都做对的概率是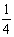 .
.
(1)求乙、丙两人各自做对这道题的概率;
(2)求做对该题人数随机变量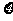 的分布列和E
的分布列和E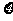 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com