
22. After many years of hard work, his dream _________ at last.
A. come true B. was come true C. was realized D. realized
第一节:单项填空(共15小题;每小题1分,满分15分)
从A、B、C、D四个选项中,选出可以填入空白处的最佳选项。
21. Despite the fact that there are a lot of complaints about ________ CCTV’s annual Spring Festival Gala(Chunwan),most people think it was really ________ feast for our eyes this year.
A. /; a B. the; the C. the; / D. / ; /
21.解:(1) 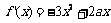 ,据题意
,据题意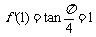
∴ 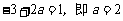 .
.
(2) 由 (1) 知,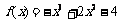 ,则
,则
|
x |
– 1 |
(– 1,0) |
0 |
(0,1) |
1 |
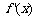 |
– 7 |
- |
0 |
+ |
1 |
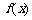 |
– 1 |
↘ |
– 4 |
↗ |
– 3 |
∴ 对于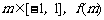 的最小值为
的最小值为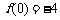
∵  的对称轴为
的对称轴为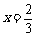 ,且抛物线开口向下,
,且抛物线开口向下,
∴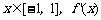 的最小值为
的最小值为 中较小的
中较小的
∵ 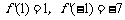
∴ 当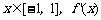 的最小值为 – 7
的最小值为 – 7
当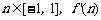 的最小值为 – 7
的最小值为 – 7
∴ 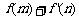 的最小值为 – 11
的最小值为 – 11

20.解:(1) 第r + 1项项系数为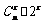 ,第r项系数为
,第r项系数为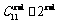 ,第r + 2项系数为
,第r + 2项系数为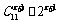
 ∴
展开式中系数最大的项为
∴
展开式中系数最大的项为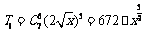
18.解:(1) 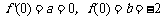
(2) 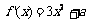
当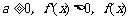 在R上递增,满足题意;
在R上递增,满足题意;
当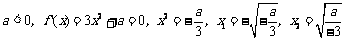
∴ 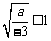 , ∴
, ∴ 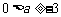
∴ 综上,a的取值范围是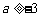 .
.
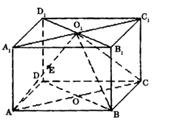 19.解法一:
19.解法一:
(1) 过O作OF⊥BC于F,连接O1F,
∵OO1⊥面AC,∴BC⊥O1F,
∴∠O1FO是二面角O1-BC-D的平面角,······················· 3分
∵OB = 2,∠OBF = 60°,∴OF =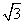 .
.
在Rt△O1OF中,tan∠O1FO =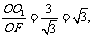
∴∠O1FO=60° 即二面角O1-BC-D的大小为60°·············································· 6分
(2) 在△O1AC中,OE是△O1AC的中位线,∴OE∥O1C
∴OE∥O1BC,∵BC⊥面O1OF,∴面O1BC⊥面O1OF,交线O1F.
过O作OH⊥O1F于H,则OH是点O到面O1BC的距离,································· 10分
∴OH =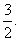 ∴点E到面O1
∴点E到面O1 BC的距离等于
BC的距离等于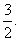 ····················································· 12分
····················································· 12分
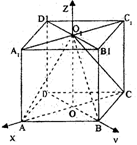 解法二:
解法二:
(1) ∵OO1⊥平面AC,
∴OO1⊥OA,OO1⊥OB,又OA⊥OB,······················· 2分
建立如图所示的空 间直角坐标系(如图)
间直角坐标系(如图)
∵底面ABCD是边长为4,∠DAB = 60°的菱形,
∴OA = 2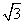 ,OB = 2,
,OB = 2,
则A(2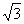 ,0,0),B(0,2,0),C(-2
,0,0),B(0,2,0),C(-2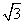 ,0,0),O1(0,0,3)·········· 3分
,0,0),O1(0,0,3)·········· 3分
设平面O1BC的法向量为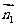 =(x,y,z),则
=(x,y,z),则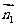 ⊥
⊥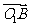 ,
,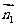 ⊥
⊥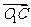 ,
,
∴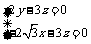 ,则z = 2,则x=-
,则z = 2,则x=-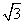 ,y = 3,
,y = 3,
∴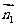 =(-
=(-
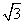 ,3,2),而平面AC的法向量
,3,2),而平面AC的法向量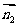 =(0,0,3)··························· 5分
=(0,0,3)··························· 5分
∴ cos<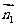 ,
,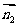 >=
>=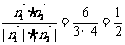 ,
,
设O1-BC-D的平面角为α,
∴cosα=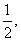 ∴α=60°.
∴α=60°.
故二面角O1-BC-D为60°.············································································· 6分
(2) 设点E到平面O1BC的距离为d,
∵E是O1A的中点,∴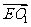 =(-
=(-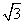 ,0,
,0,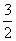 ),············································· 9分
),············································· 9分
则d=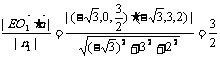
∴点E到面O1BC的距离等于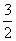 .··································································· 12分
.··································································· 12分
17.解:(1) 法一:设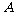 、
、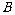 两项技术指标达标的概率分别为
两项技术指标达标的概率分别为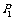 、
、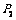
由题意得: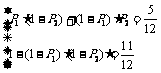 ······················································ 3分
······················································ 3分
解得: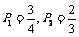 或
或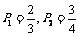 ,∴
,∴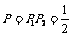 .
.
即,一个零件经过检测为合格品的概率为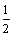 .·············································· 6分
.·············································· 6分
法二: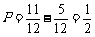
(2) 任意抽出5个零件进行检查,其中至多3个零件是合格品的概率为
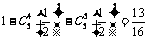 ············································································· 13分
············································································· 13分
21.(本小题满分12分)
已知函数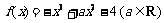 .
.
(1)
若函数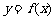 的图象在点P(1,
的图象在点P(1,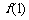 )处的切线的倾斜角为
)处的切线的倾斜角为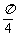 ,求实数a的值;
,求实数a的值;
(2)
设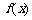 的导函数是
的导函数是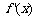 ,在 (1) 的条件下,若
,在 (1) 的条件下,若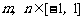 ,求
,求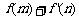 的最小值.
的最小值.
(3)
若存在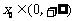 ,使
,使 ,求a的取值范围.
,求a的取值范围.
(命题人:周 静 审题人:赵文丽)
 ∴ a的取值范围为
∴ a的取值范围为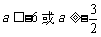
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com