3．默写古诗文名句，并写出相应的作家、篇名。(10分)

　 ①学而时习之，不亦说乎?　 　　▲　 　　，不亦乐乎?　　　　　　 (《<论语>八则》)

　 ②　　　 ▲　　　 ，长河落日圆。　　　　　　　　　　　 (　 　▲　 　《使至塞上》)

　 ③感时花溅泪，　　　 ▲　　　 。　　　　　　　　　　　　 　　　　(杜甫《春望》)

　 ④　　　 ▲　　　 ，却话巴山夜雨时。　　　　　　　　　　 (李商隐《　　 ▲　　 》)

　 ⑤　　　 ▲　　　 ，月如钩。寂寞梧桐深院锁清秋。　　　　　　　 (李煜《相见欢》)

　 ⑥落红不是无情物，　　　 ▲　　　 。　　　　　　　　　　　 (龚自珍《已亥杂诗》)

　 ⑦予独爱莲之　　　 ▲　　　 ，濯清涟而不妖……　　　　　　　 (周敦颐《爱莲说》)

　 ⑧而或长烟一空，皓月千里，　　 ▲　　 ，　　 ▲　　 ……　　 (范仲淹《岳阳楼记》)

2．下面的句子中每句都有两个错别字，把它们找出来填入表中，然后改正。(4分)

　 ①如此说来，“孤城寡人”并不正常，虽然，已经司空见惯，习以为长了，倒是“与狼共舞”这个漂亮而荒涎的词组更具有现代意识。

　 ②无学问的智慧，只是浮光略影，瞬起瞬灭的。好像肥皂泡一祥，尽管可以五光十色，但是一触即破。惟有从学问中锻炼出来的智慧，才不是瞬息幻灭的肥皂泡。

1．根据汉语拼音写出汉字。(4分)

　 ①晶　 ▲　 (yíng)　 ②玲　 ▲　 (lóng) 　③千　 ▲　 (zī)百态　 ④郑重其　 ▲　 (shì)

12．如图8－2－30所示，在真空中半径r＝3.0×10^{－2 m}的圆形区域内，有磁感应强度B＝0.2 T，方向如图的匀强磁场，一批带正电的粒子以初速度v₀＝1.0×10⁶ m/s，从磁场边界上直径ab的一端a沿着各个方向射入磁场，且初速度方向与磁场方向都垂直，该粒子的比荷为q/m＝1.0×10⁸ C/kg，不计粒子重力．求：

　 (1)粒子的轨迹半径；

　 (2)粒子在磁场中运动的最长时间；

　 (3)若射入磁场的速度改为v₀′＝3.0×10⁵ m/s，其他条件不变，试用斜线画出该批粒子在磁场中可能出现的区域．(sin 37°＝0.6，cos 37°＝0.8)

　 解析：(1)由牛顿第二定律可求得粒子在磁场中运动的半径．qv₀B＝m，R＝＝5.0×10^－2 m.

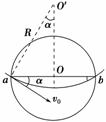　 (2)由于R>r，要使粒子在磁场中运动的时间最长，则粒子在磁场中运动的圆弧所对应的弧长最长，从右图中可以看出，以直径ab为弦、R为半径所作的圆周，粒子运动时间最长，T＝，运动时间t_m＝×T＝，

　 又sin α＝＝，所以t_m＝6.5×10^－8 s.

　 (3)R′＝＝1.5×10^－2 m，粒子在磁场中可能出现的区域见答案图所示(以aO为直径的半圆加上以a为圆心，aO为半径所作圆与磁场相交的部分)．

　 答案：(1)5.0×10^－2 m　(2)6.5×10^－8 s

　 (3)

11.

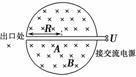
图8－2－29

　 (2009·江苏，14)1932年，劳伦斯和利文斯顿设计出了回旋加速器．回旋加速器的工作原理如图8－2－29所示，置于高真空中的D形金属盒半径为R，两盒间的狭缝很小，带电粒子穿过的时间可以忽略不计．磁感应强度为B的匀强磁场与盒面垂直．A处粒子源产生的粒子，质量为m、电荷量为+q，在加速器中被加速，加速电压为U.加速过程中不考虑相对论效应和重力作用．

　 (1)求粒子第2次和第1次经过两D形盒间狭缝后轨道半径之比；

　 (2)求粒子从静止开始加速到出口处所需的时间t；

　 (3)实际使用中，磁感应强度和加速电场频率都有最大值的限制．若某一加速器磁感应强度和加速电场频率的最大值分别为B_m、f_m，试讨论粒子能获得的最大动能E_km.

　 解析：(1)设粒子第1次经过狭缝后的半径为r₁，速度为v₁

　 qU＝mv，qv₁B＝m，解得r₁＝

　 同理，粒子第2次经过狭缝后的半径r₂＝ ，则r₂∶r₁＝∶1.

　 (2)设粒子到出口处被加速了n圈

　 2nqU＝mv²，qvB＝m，T＝，t＝nT，解得t＝.

　 (3)加速电场的频率应等于粒子在磁场中做圆周运动的频率，即f＝

　 当磁感应强度为B_m时，加速电场的频率应为fB_m＝，粒子的动能E_k＝mv²

　 当fB_m≤f_m时，粒子的最大动能由B_m决定，qv_mB_m＝m)，解得E_km＝.

　 当fB_m≥f_m时，粒子的最大动能由f_m决定，v_m＝2πf_mR，解得E_km＝2π²mfR².

　 答案：(1)∶1　(2)

　 (3)当fB_m≤f_m时，E_km＝；当fB_m≥f_m时，E_km＝2π²mfR²

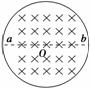
图8－2－30

10.

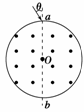
图8－2－28

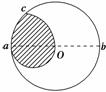
　 如图8－2－28所示是某离子速度选择器的原理示意图，在横截面半径r＝10 cm的圆形区域内有磁感应强度B＝1×10^－4 T的匀强磁场，磁场方向平行于柱形圆筒的轴线，在圆柱形筒壁上某一直径两端开有两个小孔a、b，分别作为离子的入射孔和出射孔．现有一束比荷为＝2×10¹¹ C/kg的正离子，从a孔射入，正离子射入的角度不同，最后能从b孔射出的离子速度大小就不同，其中入射角θ＝30°，且不与筒壁碰撞而从出射孔射出的离子的速度大小为(　)

　 A．4×10⁵ m/s　 　　　B．2×10⁵ m/s

　 C．4×10⁶ m/s　 　　　D．2×10⁶ m/s

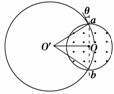
　 解析：画出离子运动轨迹所在的圆，如右图所示

　 作半径R、圆心O′，由圆的性质可知三角形abO′是等边三角形，即半径R＝2r＝0.2 m，由qvB＝m得v＝＝2×10¹¹×1×10^－4×0.2 m/s＝4×10⁶ m/s.

　 答案：C

9.

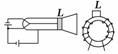
图8－2－27

　 如图8－2－27所示，为电视机显像管及其偏转线圈L的示意图．如果发现电视画面的幅度比正常时偏小，不可能是下列哪些原因引起的(　)

　 A．电子枪发射能力减弱，电子数减小

　 B．加速电场的电压过高，电子速率偏大

　 C．偏转线圈匝间短路，线圈匝数减小

　 D．偏转线圈的电流过小，偏转磁场减弱

　 解析：画面变小是由于电子束的偏转角减小，即偏转轨道半径变大造成的．根据轨道半径公式R＝，因为加速电压增大，将引起v增大，而偏转线圈匝数或电流减小，都会引起B减小，从而使轨道半径增大，偏转角减小画面变小．

　 答案：A

8．如图8－2－26所示为一个质量为m、电荷量为+q的圆环，可在水平放置的足够长的粗糙细杆上滑动，细杆处于磁感应强度为B的匀强磁场中，现给圆环向右的初速度v₀，在以后的运动过程中，圆环运动的速度图象可能是下图中的(　)

　 解析：给圆环向右的初速度v₀，圆环运动有三种可能性，若Bv₀q＝mg时，圆环做匀速直线运动，故A项正确．若v>v₀时，圆环与杆下边有摩擦力作用，摩擦力逐渐减小，运动加速度逐渐减小，最终为零，Bvq＝mg时，圆环做匀速直线运动，故D项正确．若v<v₀时，圆环与杆上边有摩擦力作用，洛伦兹力减小，摩擦力增大，加速度逐渐增大的减速运动，直至停止，故C项错．

　 答案：AD

7.

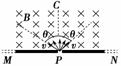
图8－2－25

　 如图8－2－25所示，在屏MN的上方有磁感应强度为B的匀强磁场，磁场方向垂直纸面向里．P为屏上的一个小孔．PC与MN垂直．一群质量为m、带电量为－q的粒子(不计重力)，以相同的速率v，从P处沿垂直于磁场的方向射入磁场区域．粒子入射方向在与磁场B垂直的平面内，且散开在与PC夹角为θ的范围内．则在屏MN上被粒子打中的区域的长度为(　)

　 A.　 　　　　　　　　B.

　 C.　 　　　　D.

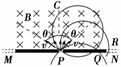
　 解析：由图可知，沿PC方向射入磁场中的带负电的粒子打在MN上的点离P点最远，为PR＝，沿两边界线射入磁场中的带负电的粒子打在MN上的点离P点最近为：PQ＝cos θ，故在屏MN上被粒子打中的区域的长度为：QR＝PR－PQ＝，选项D正确．

　 答案：D

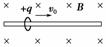
图8－2－26