
8.在加人铝粉能放出H2的无色溶液,可能大量共存的离子组是 ( )
A.NH 、Na+、NO
、Na+、NO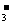 、S2- B.Na+、K+、CH3COO一、HCO
、S2- B.Na+、K+、CH3COO一、HCO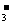
C.K+、NO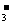 、SO
、SO 、Cl- D.K+、Al3+、MnO
、Cl- D.K+、Al3+、MnO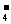 、NO
、NO
7.下列装置或操作能达到实验目的的是 ( )

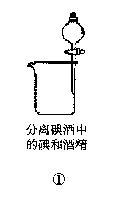
A.①②③④ B.②④ C.②③④ D.①③
6.下列说法正确的是 ( )
①世博会中国馆一一“东方之冠”使用的钢筋混凝土属于高分子化合物;
②CH3COONa、BaSO4一都是强电解质;
③明矾和氯气可用于饮用水的净化和杀菌消毒,且两者的作用原理不同:
④0.1mol/L NaOH溶液与0.1 mol/L Ba(OH)2溶液的pH相同;
⑤一定温度下,适量CO2分别通入饱和碳酸钠溶液和澄清石灰水中,都会出现浑浊。
A.①③④ B.①②④ C.②③⑤ D.③④⑤
5.以下对生物进化的叙述,正确的是 ( )
A.二倍体生物用秋水仙素处理形成四倍体,二者之间不存在生殖隔离
B.物种之间的共同进化都是通过物种之间的生存斗争实现的
C.不同物种之间、生物与环境之间共同进化导致生物多样性
D.突变和基因重组都会引起种群基因频率的定向改变
4.为研究某种药物对人体细胞的毒害作用,研究人员以哺乳动物组织块为材料进行实验,得到下表结果,下列实验分析正确的是 ( )
|
培养瓶编号 |
1 |
2 |
3 |
4 |
5 |
|
药物浓度(mg/L) |
10 |
50 |
100 |
300 |
900 |
|
变异细胞比例 |
0 |
1/106 |
1/106 |
2/106 |
8/106 |
A.安验应在氧气充足,25℃环境条件下进行
B.可利用显微镜观察或稀释涂布平板法进行计数
C.实验结果表明浓度低于50mg/L时该药物对细胞没有毒害作用
D.实验还需设置一个不加药物的空白对照组
2.下列有关人体细胞分裂的叙述,正确的是 ( )
A.有丝分裂与减数分裂相比基因突变和基因重组的概率增加
B.减数第二次分裂前期细胞中的DNA数目与有丝分裂中期的相同
C.减数第二次分裂的细胞中无同源染色体,染色体数都为23个
D.减数第一次分裂后期与减数第二次分裂后期细胞中都有两个染色体组
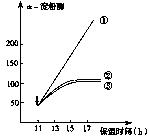 3.植物激素中的赤霉素能诱导
3.植物激素中的赤霉素能诱导 一淀粉酶的产生,促进种子萌发;6一甲基嘌呤是mRNA合成的抑制剂。分别用三组淡剂对种子进行处理:①赤霉素;②赤霉素和脱落酸;③赤霉素和6一甲基嘌呤(6一甲基嘌呤在第1l小时加入,见图中“↓”)。结果如图所示,下列说法不正确的是( )
一淀粉酶的产生,促进种子萌发;6一甲基嘌呤是mRNA合成的抑制剂。分别用三组淡剂对种子进行处理:①赤霉素;②赤霉素和脱落酸;③赤霉素和6一甲基嘌呤(6一甲基嘌呤在第1l小时加入,见图中“↓”)。结果如图所示,下列说法不正确的是( )
A.6一甲基嘌呤可抑制tt一淀粉酶的产生
B.对Q一淀粉酶的合战,脱落酸与赤霉素表现为拮抗作用
C.脱落酸作用机理是促进mRNA的合成
D.种子的萌发受多种激素共同调节
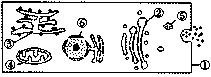
1.右图表示某动物细胞合成的分泌蛋白运输到细胞外的过程示意图。下列叙述不正确的是
 ( )
( )
A.②、③膜的组成成分和结构相似
B.分泌蛋白的分泌借助膜的选择透过性来完成
C.此围所示各种膜中糖蛋白含量最高的可能是①
D.细胞内许多生化反应部是在生物膜内或膜表面
进行的
2010.5
本试卷分第I卷(选择题)和第Ⅱ卷(非选择题)两部分,第I卷1至6页,第Ⅱ卷7至14页,共300分。考试时长150分钟。考生务必将答案答在答题卡上,在试卷上作答无效。考试结束后,将本试卷和答题卡一并交回。
以下数据可供解题时参考:
可能用到的相对原子质量:H 1 C 12 N 14 0 16 S 32 Zn 65
第I卷(选择题 共120分)
本卷共20小题,每小题6分,共120分。在每小题列出的四个选项中,选出符合题目要求的一项。
(15)(本小题共12分)
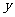
 如图,在平面直角坐标系
如图,在平面直角坐标系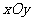 中,以
中,以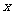 轴为始边作两个锐角
轴为始边作两个锐角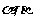 ,它们的终边分别与单位圆交于
,它们的终边分别与单位圆交于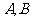 两点.已知
两点.已知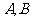 的横坐标分别为
的横坐标分别为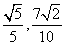 .
.
(Ⅰ)求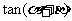 的值;
的值;
(Ⅱ)求 的值.
的值.
(16)(本小题共14分)
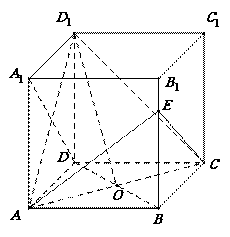 正方体
正方体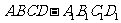 的棱长为
的棱长为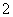 ,
, 是
是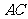 与
与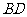 的交点,
的交点,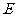 是
是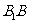 上一点,且
上一点,且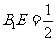 .
.
(Ⅰ)求证: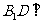 平面
平面 ;
;
(Ⅱ)求异面直线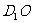 与
与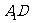 所成角的余弦值;
所成角的余弦值;
(Ⅲ)求直线 与平面
与平面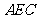 所成角的正弦值.
所成角的正弦值.
(17)(本小题共13分)
某学校高一年级开设了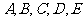 五门选修课.为了培养学生的兴趣爱好,要求每个学生必须参加且只能选修一门课程.假设某班甲、乙、丙三名学生对这五门课程的选择是等可能的.
五门选修课.为了培养学生的兴趣爱好,要求每个学生必须参加且只能选修一门课程.假设某班甲、乙、丙三名学生对这五门课程的选择是等可能的.
(Ⅰ)求甲、乙、丙三名学生参加五门选修课的所有选法种数;
(Ⅱ)求甲、乙、丙三名学生中至少有两名学生选修同一门课程的概率;
(Ⅲ)设随机变量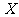 为甲、乙、丙这三名学生参加
为甲、乙、丙这三名学生参加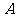 课程的人数,求
课程的人数,求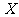 的分布列与数学期望.
的分布列与数学期望.
(18)(本小题共14分)
设函数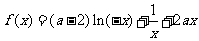 (
(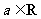 ).
).
(Ⅰ)当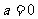 时,求
时,求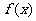 的极值;
的极值;
(Ⅱ)当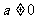 时,求
时,求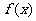 的单调区间.
的单调区间.
(19)(本小题共14分)
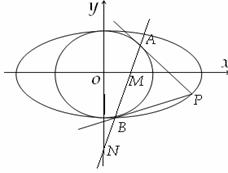
已知椭圆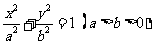 和圆
和圆 :
: ,过椭圆上一点
,过椭圆上一点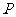 引圆
引圆 的两条切线,切点分别为
的两条切线,切点分别为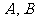 .
.
(Ⅰ)(ⅰ)若圆 过椭圆的两个焦点,求椭圆的离心率
过椭圆的两个焦点,求椭圆的离心率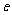 ;
;
(ⅱ)若椭圆上存在点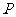 ,使得
,使得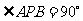 ,求椭圆离心率
,求椭圆离心率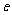 的取值范围;
的取值范围;
(Ⅱ)设直线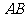 与
与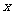 轴、
轴、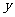 轴分别交于点
轴分别交于点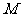 ,
,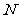 ,求证:
,求证: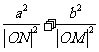 为定值.
为定值.
(20)(本小题共13分)
设集合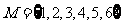 ,对于
,对于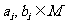 ,记
,记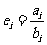 且
且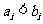 ,由所有
,由所有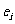 组成的集合设为
组成的集合设为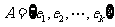 .
.
(Ⅰ)求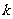 的值;
的值;
(Ⅱ)设集合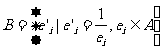 ,对任意
,对任意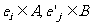 ,试求
,试求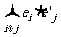 ;
;
(Ⅲ)设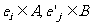 ,试求
,试求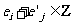 的概率.
的概率.
(考生务必将答案答在答题卡上,在试卷上作答无效)
崇文区2009-2010学年度第二学期统一练习(二)
 (9)函数
(9)函数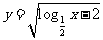 的定义域为 .
的定义域为 .
(10)如图,⊙ 中的弦
中的弦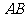 与直径
与直径 相交于
相交于
点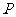 ,
,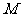 为
为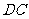 延长线上一点,
延长线上一点,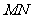 为
为
⊙ 的切线,
的切线,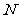 为切点,若
为切点,若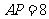 ,
,
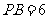 ,
,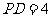 ,
,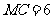 ,
,
则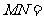 .
.
(11)甲、乙、丙三名射击运动员在某次测试中各射击20次,三人的测试成绩如下表
|
|
|
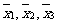 分别表示甲、乙、丙三名运动员这次测试成绩的平均数,则
分别表示甲、乙、丙三名运动员这次测试成绩的平均数,则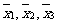 的大小关系为
;
的大小关系为
;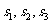 分别表示甲、乙、丙三名运动员这次测试成绩的标准差,则
分别表示甲、乙、丙三名运动员这次测试成绩的标准差,则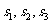 的大小关系为
.
的大小关系为
.
(12)若直线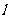 的参数方程为
的参数方程为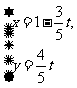 (
(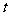 为参数),则直线
为参数),则直线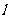 的斜率为 ;
的斜率为 ;
在极坐标系中,直线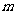 的方程为
的方程为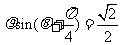 ,则点
,则点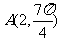 到直线
到直线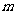 的距离为 ______.
的距离为 ______.
(13)给定下列四个命题:
①若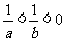 ,则
,则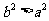 ;
;
②已知直线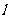 ,平面
,平面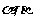 为不重合的两个平面.若
为不重合的两个平面.若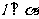 ,且
,且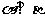 ,则
,则 ∥
∥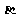 ;
;
③若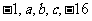 成等比数列,则
成等比数列,则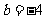 ;
;
④若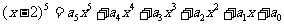 ,则
,则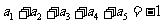 .
.
其中为真命题的是 .(写出所有真命题的序号)
(14)设不等式组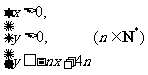 ,所表示的平面区域
,所表示的平面区域 的整点个数为
的整点个数为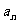 ,则
,则
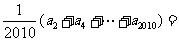 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com