
3.以原点为圆心,且截直线3x+4y+15=0所得弦长为8的圆的方程是( )
A.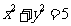 B.
B.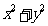 =25 C.
=25 C.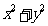 =4 D.
=4 D.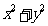 =16
=16
2.已知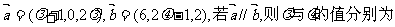 ( )
( )
A.5,2 B.
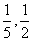 C.
C.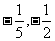 D.-5,-2
D.-5,-2
1.过点M(-4,3)和N(-2,1)的直线方程是( )
A.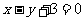 B.
B.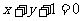 C.
C.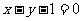 D.
D.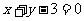
9.D
[解析]画出图形,设动点A与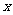 轴正方向夹角为
轴正方向夹角为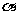 ,则
,则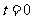 时
时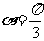 ,每秒钟旋转
,每秒钟旋转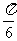 ,在
,在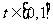 上
上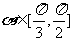 ,在
,在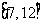 上
上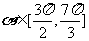 ,动点
,动点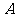 的纵坐标
的纵坐标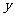 关于
关于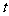 都是单调
都是单调 递增的。
递增的。
[方法技巧]由动点 在圆
在圆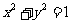 上绕坐标原点沿逆时针方向匀速旋转,可知与三角函数的定义类似,
上绕坐标原点沿逆时针方向匀速旋转,可知与三角函数的定义类似, 由12秒旋转一周能求每秒钟所转的弧度,画出单位圆,很容易看出,当t在
由12秒旋转一周能求每秒钟所转的弧度,画出单位圆,很容易看出,当t在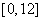 变化时,点
变化时,点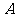 的纵坐标
的纵坐标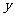 关于
关于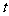 (单位:秒)的函数的单调性的变化,从而得单调递增区间.
(单位:秒)的函数的单调性的变化,从而得单调递增区间.
1. (2010安徽理数)9、动点 在圆
在圆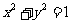 上绕坐
上绕坐 标原点沿逆时针方向匀速旋转,12秒旋转一周。已知时间
标原点沿逆时针方向匀速旋转,12秒旋转一周。已知时间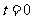 时,点
时,点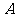 的坐标是
的坐标是 ,则当
,则当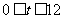 时,动点
时,动点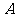 的纵坐标
的纵坐标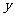 关于
关于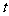 (单位:秒)的函数的单调递增区间是
(单位:秒)的函数的单调递增区间是
A、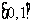 B、
B、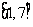 C、
C、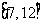 D、
D、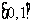 和
和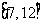
4.A
[解析]设直线方程为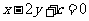 ,又经过
,又经过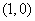 ,故
,故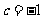 ,所求方程为
,所求方程为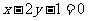 .
.
[方法技巧]因为所求直线与与直线x-2y-2=0平行,所以设平行直线系方程为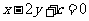 ,代入此直线所过的点的坐标,得参数值,进而得直线方程.也可以用验证法,判断四个选项中方程哪一个过点(1,0)且与直线x-2y-2=0平行.
,代入此直线所过的点的坐标,得参数值,进而得直线方程.也可以用验证法,判断四个选项中方程哪一个过点(1,0)且与直线x-2y-2=0平行.
(2010重庆文数)(8)若直线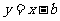 与曲线
与曲线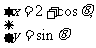 (
(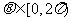 )有两个不同的公共点,则实数
)有两个不同的公共点,则实数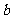 的取值范围为
的取值范围为
(A)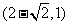
 (B)
(B)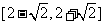
(C)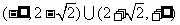 (D)
(D)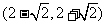
解析: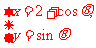 化为普通方程
化为普通方程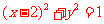 ,表
,表 示圆,
示圆,
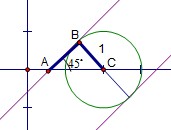 因为直线与圆
因为直线与圆 有两个不同的交点,所以
有两个不同的交点,所以 解得
解得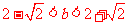 法2:利用数形结合进行分析得
法2:利用数形结合进行分析得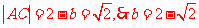
同理分析,可知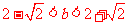
(2010重庆理数)(8) 直线y=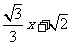 与圆心为D的圆
与圆心为D的圆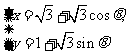
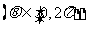 交与A、B两点,则直线AD与BD的倾斜角之和为
交与A、B两点,则直线AD与BD的倾斜角之和为
 A.
A.  B.
B. 
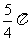 C.
C. 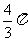 D.
D. 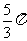
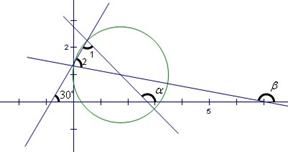
解析:数形结合
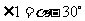
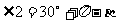
由圆的性质可知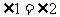
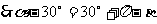
故
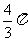
(2010广东文数)

(2010全国卷1理数)(11)已知圆O的半径为1,PA、PB为该圆的两条切线,A、B为两切点,那么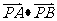 的最小值为
的最小值为
(A) 
 (
( B)
B) (C)
(C)  (D)
(D)

8.(2010江西理数)直线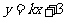 与圆
与圆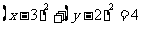 相交于M
相交于M ,N两点,若
,N两点,若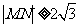 ,则k的取值范围是
,则k的取值范围是
A. 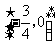 B.
B.
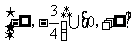 C.
C. 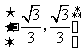 D.
D.
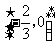

[答案]A
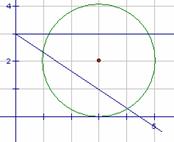 [解析]考查直线与圆的位置关系、点到直
[解析]考查直线与圆的位置关系、点到直 线距离公式,重点考察数形结合的运用.
线距离公式,重点考察数形结合的运用.
解法1: 圆心的坐标为(3.,2),且圆与y轴相切.当
圆心的坐标为(3.,2),且圆与y轴相切.当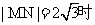 ,由点到直线距离公式,解得
,由点到直线距离公式,解得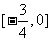 ;
;
解法2:数形结合,如图由垂径定理得夹在两直线之间即可, 不取 ,排除B,考虑区间不对称,排除C,利用斜率估值,选A
,排除B,考虑区间不对称,排除C,利用斜率估值,选A
(2010安徽文数)(4)过点(1,0)且与直线x-2y-2=0平行的直线 方程是
方程是
(A)x-2y-1=0
(B)x-2y+1=0
(C)2x+y-2=0  (D)x+2y-1=0
(D)x+2y-1=0
11.(1)用斜线给下面文言文中加波浪的部分断句。(3分)
子厚前时少年,勇于为人,不自贵重顾藉,谓功业可立就故坐废退既退又无相知有气力得位者推挽故卒死于穷裔材不为世用道不行于时也。(取材于韩愈《柳子厚墓志铭》)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com