
17.(本小题满分12分)
解:(Ⅰ)由题意得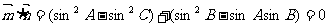
即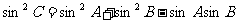 --------------------------2分
--------------------------2分
由正弦定理得 --------------------------3分
--------------------------3分
再由余弦定理得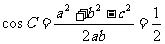
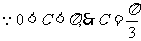 --------------------------5分
--------------------------5分
(Ⅱ)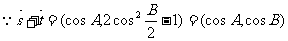 --------------------------6分
--------------------------6分

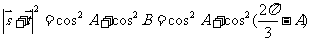
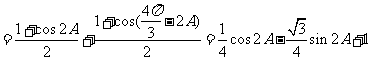 -----------------------8分
-----------------------8分
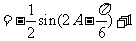 --------------------------10分
--------------------------10分
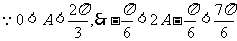
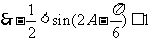
所以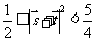 ,故
,故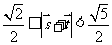 . --------------------------12分
. --------------------------12分
13.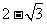 ;14.
;14. 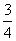
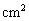 ;15.
;15. ; 16.
; 16. 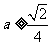 .
.
DABBB, CCBCD, AC
22.(本小题满分14分)
已知动圆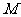 过定点
过定点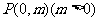 ,且与定直线
,且与定直线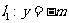 相切,动圆圆心
相切,动圆圆心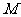 的轨迹为
的轨迹为 ,直线
,直线 过点
过点 交曲线
交曲线 于
于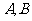 两点.
两点.
(Ⅰ)求曲线 的方程;
的方程;
(Ⅱ)若 交
交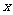 轴于点
轴于点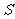 ,且
,且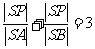 ,求
,求 的方程;
的方程;
(Ⅲ)若 的倾斜角为
的倾斜角为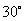 ,在
,在 上是否存在点
上是否存在点 使
使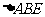 为正三角形? 若能,求点
为正三角形? 若能,求点 的坐标;若不能,说明理由.
的坐标;若不能,说明理由.
青岛市2010年高考模拟
数学试题(理)答案及评分标准 2010.5
21.(本小题满分12分)
已知函数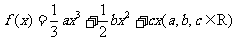 在点
在点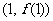 处的切线斜率为
处的切线斜率为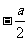 ,且
,且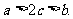
(Ⅰ)证明: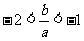 ; (Ⅱ)证明:函数
; (Ⅱ)证明:函数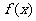 在区间
在区间 内至少有一个极值点.
内至少有一个极值点.
20.(本小题满分12分)
已知函数 的导函数
的导函数 ,数列
,数列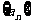 的前
的前 项和为
项和为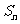 ,点
,点 均在函数
均在函数 的图象上.
的图象上.
(Ⅰ)求数列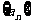 的通项公式及
的通项公式及 的最大值;
的最大值;
(Ⅱ)令 ,其中
,其中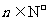 ,求
,求 的前
的前 项和.
项和.
19.(本小题满分12分)
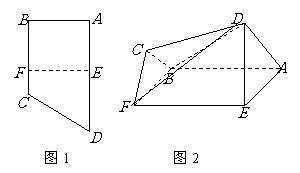 如图1,直角梯形
如图1,直角梯形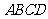 中,
中,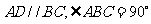 ,
,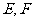 分别为边
分别为边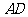 和
和 上的点,且
上的点,且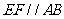 ,
,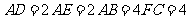 .将四边形
.将四边形 沿
沿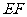 折起成如图2的位置,使
折起成如图2的位置,使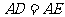 .
.
(Ⅰ)求证:
 平面
平面 ;
;
(Ⅱ)求四棱锥 的体积;
的体积;
(Ⅲ)求面 与面
与面 所成锐二面角的余弦值.
所成锐二面角的余弦值.
18.(本小题满分12分)
某中学选派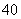 名同学参加上海世博会青年志愿者服务队(简称“青志队”),他们参加活动的次数统计如表所示.
名同学参加上海世博会青年志愿者服务队(简称“青志队”),他们参加活动的次数统计如表所示.
|
活动次数 |
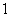 |
 |
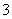 |
|
参加人数 |
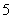 |
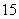 |
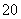 |
(Ⅰ)从“青志队”中任意选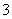 名学生,求这
名学生,求这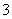 名同学中至少有
名同学中至少有 名同学参加活动次数恰好相等的概率;
名同学参加活动次数恰好相等的概率;
(Ⅱ)从“青志队”中任选两名学生,用 表示这两人参加活动次数之差的绝对值,求随机变量
表示这两人参加活动次数之差的绝对值,求随机变量
的分布列及数学期望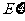 .
.
17.(本小题满分12分)
设角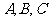 是
是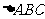 的三个内角,已知向量
的三个内角,已知向量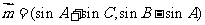 ,
,
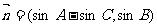 ,且
,且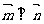 .
.
(Ⅰ)求角 的大小; (Ⅱ)若向量
的大小; (Ⅱ)若向量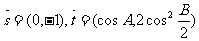 ,试求
,试求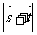 的取值范围.
的取值范围.
16.若关于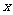 的不等式
的不等式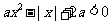 的解集为
的解集为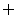 ,则实数
,则实数 的取值范围为 .
的取值范围为 .
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com