
20.(本题满分16分)
已知函数 .
.
(1)若函数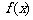 在R上是增函数,求实数
在R上是增函数,求实数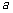 的取值范围;
的取值范围;
(2)求所有的实数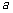 ,使得对任意
,使得对任意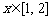 时,函数
时,函数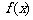 的图象恒在函数
的图象恒在函数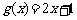
图象的下方;
(3)若存在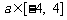 ,使得关于
,使得关于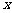 的方程
的方程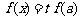 有三个不相等的实数根,求实数
有三个不相等的实数根,求实数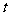 的取值范围.
的取值范围.
附加题部分:
19.(本题满分16分)
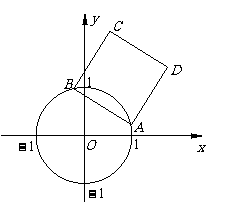
已知圆O: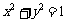 ,O为坐标原点.
,O为坐标原点.
(1)边长为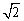 的正方形ABCD的顶点A、B均在圆O上,C、D在圆O外,当点A在圆O上运动时,C点的轨迹为E.
的正方形ABCD的顶点A、B均在圆O上,C、D在圆O外,当点A在圆O上运动时,C点的轨迹为E.
①求轨迹E的方程;
②过轨迹E上一定点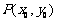 作相互垂直的两条直线
作相互垂直的两条直线 ,并且使它们分别与圆O、轨迹E相交,设
,并且使它们分别与圆O、轨迹E相交,设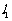 被圆O截得的弦长为
被圆O截得的弦长为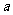 ,设
,设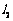 被轨迹E截得的弦长为
被轨迹E截得的弦长为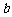 ,求
,求 的最大值.
的最大值.
(2)正方形ABCD的一边AB为圆O的一条弦,求线段OC长度的最值.
18.(本题满分16分)
设等差数列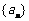 的公差为
的公差为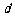 ,
,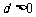 ,数列
,数列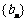 是公比为
是公比为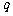 等比数列,且
等比数列,且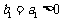 .
.
(1)若 ,
,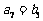 ,探究使得
,探究使得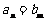 成立时
成立时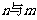 的关系;
的关系;
(2)若 ,求证:当
,求证:当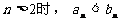 .
.
17.(本题满分14分)
在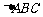 中,
中,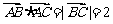 .
.
(1)求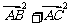 的值;
的值;
(2)求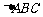 面积的最大值.
面积的最大值.
16.(本题满分14分)
在正三棱柱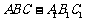 中,
中,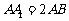 ,
,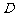 ,
,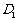 ,
,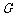 分别为
分别为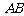 ,
,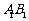 ,
,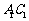 的中点,
的中点,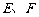 在
在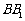 上,且
上,且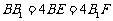 .
.
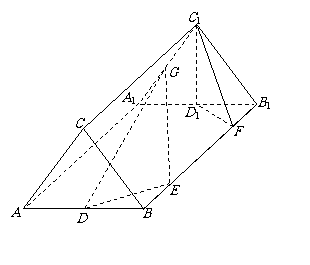 (1)求证:
(1)求证: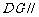 平面
平面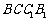 ;
;
(2)求证:平面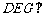 平面
平面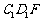 .
.
15.(本题满分14分)
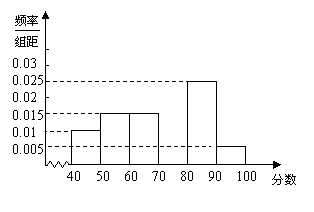
某老师从参加高一年级一次考试的学生中抽出60名学生,将其成绩(均为整数)分成六段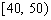 ,
,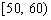 ,…
,…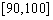 后画出如下部分频率分布直方图.观察图形的信息,回答下列问题:
后画出如下部分频率分布直方图.观察图形的信息,回答下列问题:
(1)求第四小组的频率,并补全这个频率分布直方图;
(2)该老师不小心洒了一个墨点在直方图的矩形区域内,求恰好落在第四组的小矩形内的概率(不计墨点大小);
(3)若60分及以上为及格,估计从高一年级及格的学生中抽取一位学生分数不低于80分的概率.
14. 图为函数
图为函数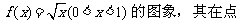
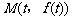
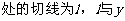 轴和直线
轴和直线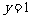 分别
分别
交于点P、Q,点N(0,1),若△PQN的面积为b
时的点M恰好有两个,则b的取值范围为 ▲ .
13.某同学在研究函数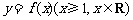 的性质,他已经正确地证明了函数
的性质,他已经正确地证明了函数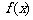 满足:
满足:
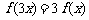 ,并且当
,并且当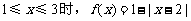 ,这样对任意
,这样对任意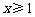 ,他都可以
,他都可以
求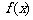 的值了,比如
的值了,比如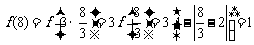 ,
,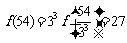 ,
,
请你根据以上信息,求出集合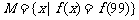 中最小的元素是 ▲ .
中最小的元素是 ▲ .
12.在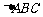 中,边
中,边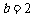 ,
,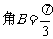 ,
,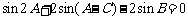 ,则边
,则边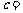 ▲ .
▲ .
11.有公共焦点的椭圆与双曲线中心为原点,焦点在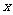 轴上,左右焦点分别为
轴上,左右焦点分别为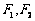 ,且
,且
它们在第一象限的交点为P,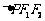 是以
是以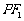 为底边的等腰三角形.若
为底边的等腰三角形.若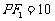 ,双曲线的离心率的取值范围为
,双曲线的离心率的取值范围为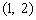 ,则该椭圆的离心率的取值范围是
▲ .
,则该椭圆的离心率的取值范围是
▲ .
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com