
5.地球表面的根本热源是 ( )
A.太阳辐射 B.大气热辐射 C.地面再辐射热 D.大气逆辐射
4.人均消费碳排放量 ( )
A.印度多于俄罗斯 B.美国最多
C.欧盟15国多于加拿大 D.日本多于美国
读图2,回答5、6题。
3.有关我国碳排放量的正确叙述是 ( )
A.消费的碳排放总量大于生产碳排放总量
B.消费本国的碳排放量小于他国的碳排放量
C.消费他国的碳排放量是由于出口产品所产生的
D.生产的碳排放量有一部分产品出口到他国被消费掉
2.图中所示,碳排放量本国消费远远超过生产的有 ( )
A.巴西、欧盟15国、墨西哥 B.加拿大、俄罗斯、美国
C.日本、欧盟15国、美国 D.中国、印度、南非
1.某游客利用春节假期到澳大利亚东部旅游,关于该时段的正确叙述是 ( )
A.太阳直射点正向南移
B.首都堪培拉的昼比北京长
C.地球公转的速度越来越快
D.悉尼(151°E)正实行夏时制,即东十区的区时减一小时
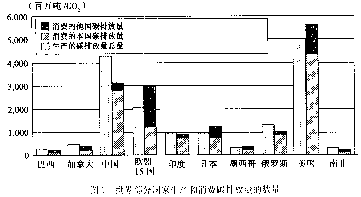 读图1,回答2~4题。
读图1,回答2~4题。
2010.5
第Ⅰ卷(单项选择题)
本卷共35小题,每小题4分,共140分。在每小题列出的四个选项中,只有一项最符合题目要求的。
(15)(本小题共12分)
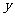
 如图,在平面直角坐标系
如图,在平面直角坐标系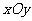 中,以
中,以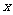 轴为始边作两个锐角
轴为始边作两个锐角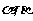 ,它们的终边分别与单位圆交于
,它们的终边分别与单位圆交于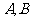 两点.已知
两点.已知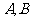 的横坐标分别为
的横坐标分别为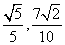 .
.
(Ⅰ)求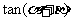 的值;
的值;
(Ⅱ)求 的值.
的值.
(16)(本小题共14分)
 正方体
正方体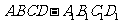 的棱长为
的棱长为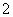 ,
, 是
是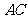 与
与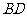 的交点,
的交点,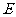 是
是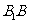 上一点,且
上一点,且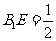 .
.
(Ⅰ)求证: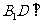 平面
平面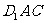 ;
;
(Ⅱ)求异面直线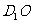 与
与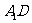 所成角的余弦值;
所成角的余弦值;
(Ⅲ)求直线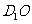 与平面
与平面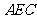 所成角的正弦值.
所成角的正弦值.
(17)(本小题共13分)
某学校高一年级开设了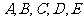 五门选修课.为了培养学生的兴趣爱好,要求每个学生必须参加且只能选修一门课程.假设某班甲、乙、丙三名学生对这五门课程的选择是等可能的.
五门选修课.为了培养学生的兴趣爱好,要求每个学生必须参加且只能选修一门课程.假设某班甲、乙、丙三名学生对这五门课程的选择是等可能的.
(Ⅰ)求甲、乙、丙三名学生参加五门选修课的所有选法种数;
(Ⅱ)求甲、乙、丙三名学生中至少有两名学生选修同一门课程的概率;
(Ⅲ)设随机变量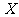 为甲、乙、丙这三名学生参加
为甲、乙、丙这三名学生参加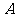 课程的人数,求
课程的人数,求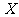 的分布列与数学期望.
的分布列与数学期望.
(18)(本小题共14分)
设函数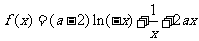 (
( ).
).
(Ⅰ)当 时,求
时,求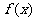 的极值;
的极值;
(Ⅱ)当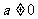 时,求
时,求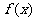 的单调区间.
的单调区间.
(19)(本小题共14分)
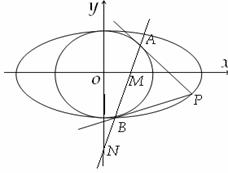
已知椭圆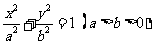 和圆
和圆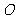 :
: ,过椭圆上一点
,过椭圆上一点 引圆
引圆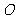 的两条切线,切点分别为
的两条切线,切点分别为 .
.
(Ⅰ)(ⅰ)若圆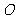 过椭圆的两个焦点,求椭圆的离心率
过椭圆的两个焦点,求椭圆的离心率 ;
;
(ⅱ)若椭圆上存在点 ,使得
,使得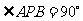 ,求椭圆离心率
,求椭圆离心率 的取值范围;
的取值范围;
(Ⅱ)设直线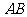 与
与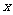 轴、
轴、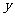 轴分别交于点
轴分别交于点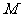 ,
,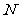 ,求证:
,求证: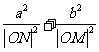 为定值.
为定值.
(20)(本小题共13分)
设集合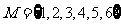 ,对于
,对于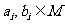 ,记
,记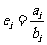 且
且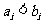 ,由所有
,由所有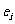 组成的集合设为
组成的集合设为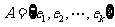 .
.
(Ⅰ)求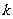 的值;
的值;
(Ⅱ)设集合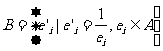 ,对任意
,对任意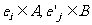 ,试求
,试求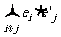 ;
;
(Ⅲ)设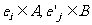 ,试求
,试求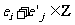 的概率.
的概率.
(考生务必将答案答在答题卡上,在试卷上作答无效)
崇文区2009-2010学年度第二学期统一练习(二)
 (9)函数
(9)函数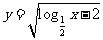 的定义域为 .
的定义域为 .
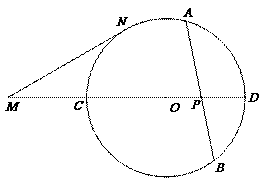
(10)如图,⊙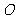 中的弦
中的弦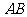 与直径
与直径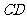 相交于
相交于
点 ,
,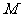 为
为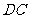 延长线上一点,
延长线上一点,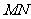 为
为
⊙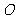 的切线,
的切线,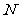 为切点,若
为切点,若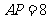 ,
,
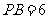 ,
,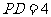 ,
,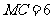 ,
,
则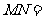 .
.
(11)甲、乙、丙三名射击运动员在某次测试中各射击20次,三人的测试成绩如下表
|
|
|
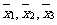 分别表示甲、乙、丙三名运动员这次测试成绩的平均数,则
分别表示甲、乙、丙三名运动员这次测试成绩的平均数,则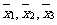 的大小关系为
;
的大小关系为
;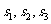 分别表示甲、乙、丙三名运动员这次测试成绩的标准差,则
分别表示甲、乙、丙三名运动员这次测试成绩的标准差,则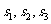 的大小关系为
.
的大小关系为
.
(12)若直线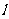 的参数方程为
的参数方程为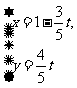 (
(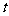 为参数),则直线
为参数),则直线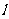 的斜率为 ;
的斜率为 ;
在极坐标系中,直线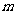 的方程为
的方程为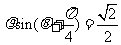 ,则点
,则点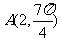 到直线
到直线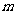 的距离为 ______.
的距离为 ______.
(13)给定下列四个命题:
①若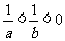 ,则
,则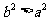 ;
;
②已知直线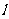 ,平面
,平面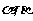 为不重合的两个平面.若
为不重合的两个平面.若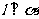 ,且
,且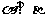 ,则
,则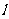 ∥
∥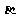 ;
;
③若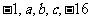 成等比数列,则
成等比数列,则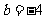 ;
;
④若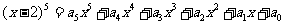 ,则
,则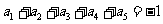 .
.
其中为真命题的是 .(写出所有真命题的序号)
(14)设不等式组 ,所表示的平面区域
,所表示的平面区域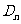 的整点个数为
的整点个数为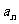 ,则
,则
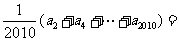 .
.
(1)“关于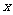 的不等式
的不等式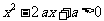 的解集为
的解集为 ”是“
”是“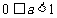 ”
”
(A)充分非必要条件 (B)必要非充分条件
(C)充分必要条件 (D)既非充分又非必要条件
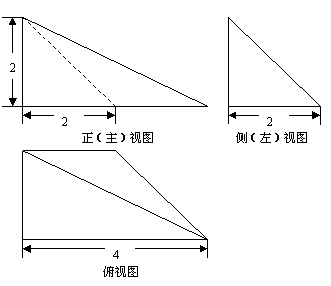 (2)一个几何体的三视图如图所示,则这个几何体的体积等于
(2)一个几何体的三视图如图所示,则这个几何体的体积等于
(A) 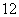 (B)
(B) 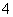 (C)
(C)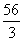 (D)
(D)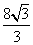
(3)设函数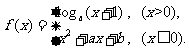 若
若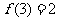 ,
,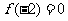 ,则
,则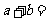
(A) 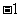 (B) 0 (C)1 (D)2
(B) 0 (C)1 (D)2
(4)把函数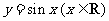 的图象上所有的点向左平移
的图象上所有的点向左平移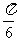 个单位长度,再把所得图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),得到的图象所表示的函数为
个单位长度,再把所得图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),得到的图象所表示的函数为
(A) (B)
(B)
(C)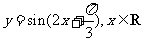 (D)
(D)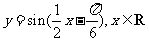
(5)已知点 是抛物线
是抛物线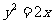 上的一个动点,则点
上的一个动点,则点 到点
到点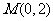 的距离与点
的距离与点 到该抛物线准线的距离之和的最小值为
到该抛物线准线的距离之和的最小值为
(A)3 (B)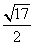 (C)
(C) (D)
(D)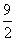
(6)若非零向量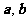 满足
满足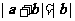 ,则
,则
(A) 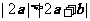 (B)
(B) 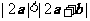
(C)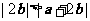 (D)
(D)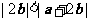
(7)用5,6,7,8,9组成没有重复数字的五位数,其中恰好有一个奇数夹在两个偶数之
间的五位数的个数为
(A)120 (B)72 (C)48 (D)36
(8)已知圆的方程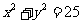 ,过
,过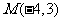 作直线
作直线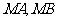 与圆交于点
与圆交于点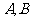 ,且
,且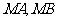 关于直线
关于直线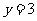 对称,则直线
对称,则直线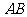 的斜率等于
的斜率等于
(A)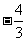 (B)
(B)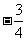 (C)
(C)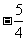 (D)
(D)
崇文区2009-2010学年度第二学期统一练习(二)
高三数学(理科) 2010.5
第Ⅱ卷(共110分)
(15)(本小题共12分)
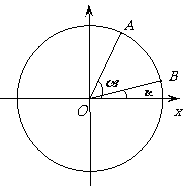 如图,在平面直角坐标系
如图,在平面直角坐标系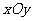 中,以
中,以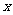 轴为始边作两个锐角
轴为始边作两个锐角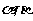 ,它们的终边分别与单位圆交于
,它们的终边分别与单位圆交于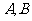 两点.已知
两点.已知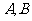 的横坐标分别为
的横坐标分别为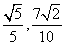 .
.
(Ⅰ)求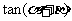 的值;
的值;
(Ⅱ)求 的值.
的值.
(16)(本小题共14分)
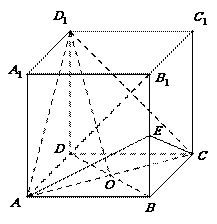 正方体
正方体 的棱长为
的棱长为 ,
, 是
是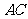 与
与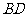 的交点,
的交点,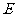 为
为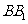 的中点.
的中点.
(Ⅰ)求证:直线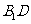 ∥平面
∥平面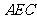 ;
;
(Ⅱ)求证: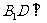 平面
平面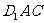 ;
;
(Ⅲ)求三棱锥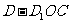 的体积.
的体积.
(17)(本小题共13分)
在平面直角坐标系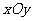 中,平面区域
中,平面区域 中的点的坐标
中的点的坐标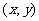 满足
满足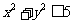 ,从区域
,从区域 中随机取点
中随机取点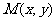 .
.
(Ⅰ)若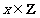 ,
,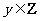 ,求点
,求点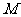 位于第四象限的概率;
位于第四象限的概率;
(Ⅱ)已知直线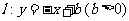 与圆
与圆 相交所截得的弦长为
相交所截得的弦长为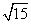 ,
,
求 的概率.
的概率.
(18)(本小题共14分)
已知函数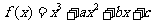 在
在 与
与 处都取得极值.
处都取得极值.
(Ⅰ)求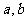 的值及函数
的值及函数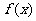 的单调区间;
的单调区间;
(Ⅱ)若对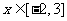 ,不等式
,不等式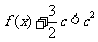 恒成立,求
恒成立,求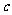 的取值范围.
的取值范围.
(19)(本小题共14分)
已知椭圆的中心在原点,焦点在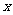 轴上,经过点
轴上,经过点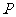
 且离心率
且离心率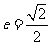 .过定点
.过定点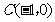 的直线与椭圆相交于
的直线与椭圆相交于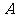 ,
,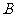 两点.
两点.
(Ⅰ)求椭圆的方程;
(Ⅱ)在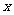 轴上是否存在点
轴上是否存在点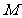 ,使
,使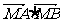 为常数?若存在,求出点
为常数?若存在,求出点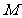 的坐标;若不存
的坐标;若不存
在,请说明理由.
(20)(本小题共13分)
已知数列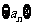 的前
的前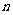 项和为
项和为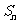 ,且满足
,且满足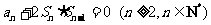 ,
,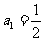 .
.
(Ⅰ)求证:{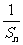 }是等差数列;
}是等差数列;
(Ⅱ)求数列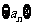 的通项公式;
的通项公式;
(Ⅲ)若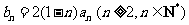 ,求证:
,求证:  .
.
(考生务必将答案答在答题卡上,在试卷上作答无效)
崇文区2009-2010学年度第二学期统一练习(二)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com