
8、解: 设M.m共同速度为v,由动量守恒得
mvB-MVA=(m+M)v
代入数据得: v=2m/s
对AB组成得系统,由能量守恒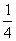
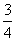 umgL=
umgL=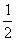 MVA2+
MVA2+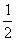 mvB2-
mvB2-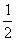 (M+m)V2
(M+m)V2
代入数据得: u=0.6
木板A与障碍物发生碰后以原速度反弹,假设B向右滑行,并与弹簧发生相互作用,当AB再次处于相对静止时,共同速度为u
由动量守恒得mv-Mv=(m+m)u 设B相对A的路程为s,由能量守恒得
umgs=(m+M)v2--( m+M)u2 代入数据得:s=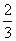 (m)
(m)
由于s>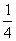 L,所以B滑过Q点并与弹簧相互作用,然后相对A向左滑动到Q点左边,设离Q点距离为s1
L,所以B滑过Q点并与弹簧相互作用,然后相对A向左滑动到Q点左边,设离Q点距离为s1
S1=s-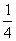 L=0.17(m)
L=0.17(m)
7、解:设平板车长为L,沙袋在车上受到的摩擦力为f。沙袋轻轻放到车上时,设最终车与沙袋的速度为v′,则
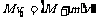
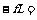
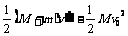
又M=
4m
可得:
设沙袋以水平向左的初速度扔到车上,显然沙袋的初速度越大,在车上滑行的距离越长,沙袋刚好不从车上落下时,相对与车滑行的距离为L,其初速度为最大初速设为v,车的最终速度设为v终,以向右为坐标的正方向,有:
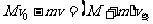
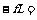
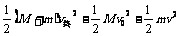
又M=
4m  可得:v=v0(v=3v0舍去)
可得:v=v0(v=3v0舍去)
车的最终速度设为v终=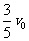 方向向左
方向向左
6、解(1)根据牛顿第二定律,滑块相对车滑动时的加速度
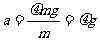 (1分)
(1分)
滑块相对车滑动的时间 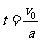 (1分)
(1分)
滑块相对车滑动的距离 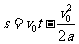 (1分)
(1分)
滑块与车摩擦产生的内能 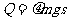 (1分)
(1分)
由上述各式解得 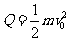 (与动摩擦因数μ无关的定值) (1分)
(与动摩擦因数μ无关的定值) (1分)
(2)设恒力F取最小值为F1,滑块加速度为a1,此时滑块恰好到达车的左端,则
滑块运动到车左端的时间 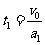 ①
①
由几何关系有 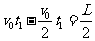 ② (1分)
② (1分)
由牛顿定律有 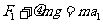 ③ (1分)
③ (1分)
由①②③式代入数据解得 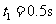 ,
,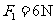 (2分)
(2分)
则恒力F大小应该满足条件是 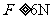 (1分)
(1分)
(3)力F取最小值,当滑块运动到车左端后,为使滑块恰不从右端滑出,相对车先做匀加速运动(设运动加速度为a2,时间为t2),再做匀减速运动(设运动加速度大小为a3).到达车右端时,与车达共同速度.则有
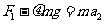 ④ (1分)
④ (1分)
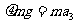 ⑤ (1分)
⑤ (1分)
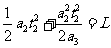 ⑥ (1分)
⑥ (1分)
由④⑤⑥式代入数据解得 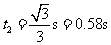 (1分)
(1分)
则力F的作用时间t应满足 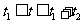 ,即
,即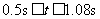 (2分)
(2分)
5、解:由图2可直接看出,A、B一起做周期性运动,运动的周期T=2t0,令 m表示 A的质量,L表示绳长,v1表示 B陷入A内时即t=0时 A、B的速度(即圆周运动最低点的速度),v2表示运动到最高点时的速度,F1表示运动到最低点时绳的拉力,f2表示运动到最高点时绳的拉力,则根据动量守恒定律,得mv0=( m0+m)v1,在最低点和最高点处运用牛顿定律可得
F1-( m0+m)g=( m0+m)v12/L, F2+( m0+m)g=( m0+m)v22/L
根据机械能守恒定律可得 2L( m+m0)g=( m+m0) v12/2- ( m+m0) v22/2。
由图2可知F2=0 。F1=Fm。由以上各式可解得,反映系统性质的物理量是
m=Fm/6g-m0 ,L =36m02v02 g/5Fm2,
A、B一起运动过程中的守恒量是机械能E,若以最低点为势能的零点,则E=(m+m0)v12/2。由几式解得E=3m02v02g/Fm。
4、弹簧继续伸长,A球离开挡板P,并获得速度。当A、D的速度相等时,弹簧伸至最长.此时的势能为最大,设此时A、D的速度为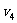 ,势能为
,势能为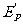 ·由动量守恒定律得
·由动量守恒定律得
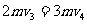 ⑤
⑤
由机械能守恒定律得: 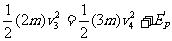 ⑥
⑥
由①、②两式联立解得: 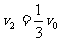 ⑦
⑦
联立①②③④⑤⑥式解得 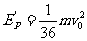 ⑧
⑧
3、撞击P后,A与D的动能都为0,当突然解除锁定后(相当于静止的A、D两物体中间为用细绳拉紧的弹簧,突然烧断细绳的状况,弹簧要对D做正功),当弹簧恢复到自然长度时,弹簧的弹性势能全部转变成D的动能,设D的速度为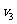 ,则有
,则有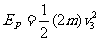 ④
④
2、当弹簧的长度被锁定时,弹簧压缩到最短,D与A速度相等,如此时速度为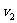 ,由动量守恒得
,由动量守恒得 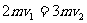 ②
②
当弹簧的长度被锁定后,D的一部分动能作为弹簧的弹性势能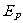 被贮存起来了.由能量守恒,有
被贮存起来了.由能量守恒,有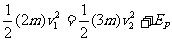 ③
③
4、解1、球C与B发生碰撞,并立即结成一个整体D,根据动量守恒,有
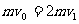 (
(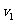 为D的速度)
①
为D的速度)
①
3、解:(1)由动能定理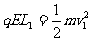
得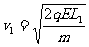 ①
①
(2)若物体碰后仍沿原方向运动,碰后滑板速度为V,
由动量守恒 得
得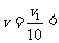 物体速度
物体速度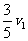 ,故不可能 ②
,故不可能 ②
∴物块碰后必反弹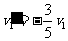 ,由动量守恒
,由动量守恒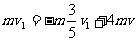 ③ 得
③ 得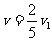 ④
④
由于碰后滑板匀速运动直至与物体第二次碰撞之前,故物体与A壁第二次碰前,滑板速度 ⑤ 。
⑤ 。
物体与A壁第二次碰前,设物块速度为v2, 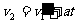 ⑥
⑥
由两物的位移关系有: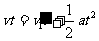 ⑦即
⑦即 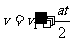 ⑧
⑧
由⑥⑧代入数据可得: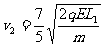 ⑨
⑨
(3)物体在两次碰撞之间位移为S, 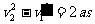
得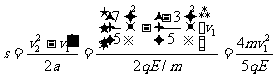
∴ 物块从开始到第二次碰撞前电场力做功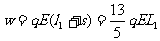
2、解:(1)B与A碰撞后,B相对A向左运动,A受摩擦力向左,而A的运动方向向右,故摩擦力对A做负功。
设B与A碰后的瞬间A的速度为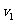 ,B的速度为
,B的速度为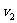 ,A、B相对静止时的共同速度为
,A、B相对静止时的共同速度为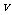 ,由动量守恒得:
,由动量守恒得: 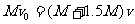 ①
①
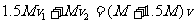 ②
②
碰后到相对静止,对A、B系统由功能关系得:
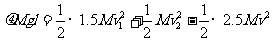 ③
③
由①②③式解得: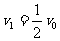 (另一解
(另一解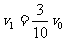 因小于
因小于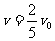 而舍去)
而舍去)
这段过程A克服摩擦力做功为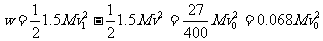 ④(2)A在运动过程中不可能向左运动,因为在B未与A碰撞之前,A受摩擦力方向向右,做加速运动,碰后A受摩擦力方向向左,做减速运动,直到最后共同速度仍向右,因此不可能向左运动。
④(2)A在运动过程中不可能向左运动,因为在B未与A碰撞之前,A受摩擦力方向向右,做加速运动,碰后A受摩擦力方向向左,做减速运动,直到最后共同速度仍向右,因此不可能向左运动。
B在碰撞之后,有可能向左运动,即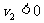 ,结合①②式得:
,结合①②式得: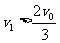 ⑤
⑤
代入③式得: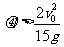 ⑥
⑥
另一方面,整个过程中损失的机械能一定大于或等于系统克服摩擦力做的功,即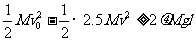 ⑦ 即
⑦ 即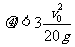
故在某一段时间里B运动方向是向左的条件是 ⑧
⑧
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com