4. 若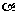、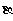是关于x的方程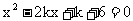的两个实根, 则的最小

值为　　　　　　　　 .

5设方程2sin²x-4asinx+1-a=0 在[0, p]上有两个不同的解,实数a 的取值范围______________________________

6若不等式2sin²x-4asinx+1-a>0 在[0, p]上恒成立,　 实数 a 的取值范围________________________________.

7已知二次函数满足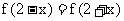, 其图象顶点为A, 图象与x轴交于点

B和C点, 且△ABC的面积为18, 写出此二次函数的解析式.

[学后反思]____________________________________________________ _______

　　　　　 _____________________________________________________________

　　　　　 _____________________________________________________________

3. 已知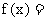x ², 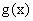是一次函数且为增函数, 若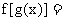 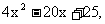则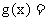

　　　　　　　　　　　 .

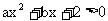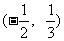2.　 不等式的解集是, 则=____________________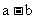　　　　　　　　　　

1. 若关于x的不等式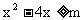对任意x∈恒成立, 则 m的范围_________________

4.常见的实根分布情况

设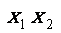为f(x)=0(a>0)的两个实根。

(1)

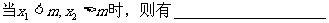
(2)当在区间(m,n)有且只有一个实根时，则有：

___________________________________________________________________________

(3) 当在区间(m,n)有两个实根时，则有：

___________________________________________________________________________

(4)当在两个区间中各有一个实根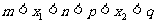时，则有

___________________________________________________________________________

[典型例析]

例1. 对于关于x的方程x²+(2m-1)x+4-2m=0 求满足下列条件的m的取值范围

(1) 两个正根　　　　　　　　　　　 (2)有两个负根

(3) 两个根都小于-1　　　　　　　　　 (4) 两个根都大于1/2

(5)一个根大于2，一个根小于2　　　　 (6) 两个根都在(0 ， 2)内

(7) 两个根有且仅有一个在(0 . 2)内　

(8)一个根在(-2 .0)内，另一个根在(1 . 3)内

(9) 一个正根，一个负根且正根绝对值较大　　　　

(10)一个根小于2，一个根大于4

反思小结：

[当堂检测]

2.一元二次函数的单调性：

　当时：　　　 为增函数；　　 为减函数；

当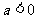时：　　　 为增函数；　　　 为减函数；

3.二次函数与一元二次方程，一元二次不等式之间的内在联系

(1)f(x)=ax²+bx+c(a≠0)的图像与x轴交点的横坐标是方程_______________的实根

(2)若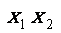为f(x)=0的实根，则f(x)在x轴上截得的线段长应为||=__________________________________________________

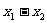(3)当_________________时，恒有f(x)>0;当____________________时，恒有f(x)<0

1.二次函数的解析式的三种形式

一般式: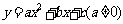；对称轴方程是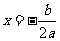；顶点为；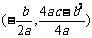

两点式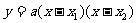：；对称轴方程是　　　 ；与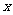轴的交点为　　　　 ；

顶点式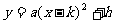：；对称轴方程是　　　　　 ；顶点为　　　　　 ；

4.　　　 以极度的热情投入学习，体会成功的快乐。

[学习重点]

基本初等函数的图像及性质。

[学习难点]

基本初等函数的图像及性质，基本函数图像的综合运用。

[自主学习]

3.　　　 体会高中数学中数形结合的思想。

2.　　　 熟练掌握二次函数的图像与性质，从而能判断一元二次方程根的存在性及根的个数。