1．物理学中引入“质点”、“点电荷”等概念的科学方法主要是

A．控制变量　　 B．理想模型　　 　C．类比　　 　D．等效替代

22.(本小题满分14分)

已知函数f (x) = log_a x (a > 0且a≠1)，若数列：2，f (a₁)，f (a₂)，…，f (a_n)，2n + 4 (n∈N^﹡)为等差数列.

(1) 求数列{a_n}的通项公式a_n；

(2) 若a = 2，b_n = a_n·f (a_n)，求数列{b_n}前n项和S_n；

(3) 在(2)的条件下对任意的n∈N^﹡，都有b_n > f ^{- 1}(t)，求实数t的取值范围.

21.(本小题满分12分)

如图所示，中心在原点，顶点A₁、A₂在x轴上，离心率为的双曲线C经过点P (6 , 6)，

动直线l经过点(0 , 1)与双曲线C交于M、N两点，Q为线段MN的中点.

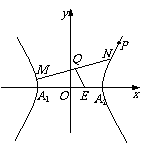(1) 求双曲线C的标准方程；

(2) 若E点为(1 , 0)，是否存在实数λ使 =λ，若存在，

求λ值；若不存在，说明理由.

20.(本小题满分12分)

已知函数y = f (x) = .

(1) 求函数f (x)的图像在x = 处的切线方程；

(2) 求y = f (x)的最大值.

19.(本小题满分12分)

如图所示，在菱形ABCD中，∠DAB = 60°，PA⊥底面ABCD，PA = AB = 2，E、F分别是AB与PD的中点.

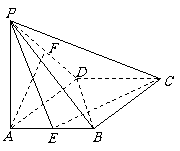(1) 求证：PC⊥BD；

(2) 求证：AF∥平面PEC；

(3) 求二面角P - EC - D的大小.

18. (本小题满分12分)

四个纪念币A、B、C、D，投掷时正面向上的概率如下表所示(0 < a < 1).

这四个纪念币同时投掷一次，设ξ表示出现正面向上的个数.

(1) 求ξ的分布列及数学期望；

(2) 在概率P (ξ= i ) (i = 0 , 1 , 2 , 3 , 4)中，若P (ξ= 2 )的值最大，求a的取值范围.

17.(本小题满分12分)

已知f (x) = 2cos² x + 2sin xcos x + a (a为常数).

(1) 求f (x)的单调递增区间；

(2) 若f (x)在区间[ - , ]上的最大值与最小值之和为3，求a的值.

16.在△ABC中，给出下列命题：

①若sin 2A = sin 2B，则△ABC是等腰三角形；

②若sin A = cos B，则△ABC是直角三角形；

③若cos Acos Bcos C < 0，则△ABC是钝角三角形；

④若cos (A - B)cos (B - C)cos (C - A) = 1，则△ABC是等边三角形；

　 其中正确的命题有 　　　　(写出所有真命题的序号).

15.已知圆C：x² + y² - 6x - 4y + 8 = 0，以圆C与坐标轴的交点分别作为双曲线的一个焦点和顶点，则适合上述条件的双曲线的标准方程为 　　　　.

14.已知函数f (x) = 在点x = 1处连续，则a = 　　　　.