3.欧姆定律

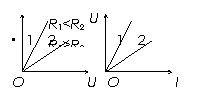
(适用于金属导体和电解液，不适用于气体导电)。

电阻的伏安特性曲线：注意I-U曲线和U-I曲线的区别。还要注意：当考虑到电阻率随温度的变化时，电阻的伏安特性曲线不再是过原点的直线。

[例1] 实验室用的小灯泡灯丝的I-U特性曲线可用以下哪个图象来表示：

解：灯丝在通电后一定会发热，当温度达到一定值时才会发出可见光，这时温度能达到很高，因此必须考虑到灯丝的电阻将随温度的变化而变化。随着电压的升高，电流增大，灯丝的电功率将会增大，温度升高，电阻率也将随之增大，电阻增大，。U越大I-U曲线上对应点于原点连线的斜率必然越小，选A。

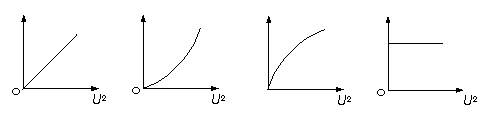
[例2]下图所列的4个图象中，最能正确地表示家庭常用的白炽电灯在不同电压下消耗的电功率P与电压平方U ²之间的函数关系的是以下哪个图象

　　 A.　　　　　　　 B.　　　　　　　 C.　　　　　　　 D.

解：此图象描述P随U ²变化的规律，由功率表达式知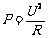：，U越大，电阻越大，图象上对应点与原点连线的斜率越小。选C。

2.电阻定律

导体的电阻R跟它的长度l成正比，跟它的横截面积S成反比。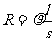

(1)ρ是反映材料导电性能的物理量，叫材料的电阻率(反映该材料的性质，不是每根具体的导线的性质)。单位是Ωžm。

(2)纯金属的电阻率小，合金的电阻率大。

⑶材料的电阻率与温度有关系：

①金属的电阻率随温度的升高而增大(可以理解为温度升高时金属原子热运动加剧，对自由电子的定向移动的阻碍增大。)铂较明显，可用于做温度计；锰铜、镍铜的电阻率几乎不随温度而变，可用于做标准电阻。

②半导体的电阻率随温度的升高而减小(可以理解为半导体靠自由电子和空穴导电，温度升高时半导体中的自由电子和空穴的数量增大，导电能力提高)。

③有些物质当温度接近0 K时，电阻率突然减小到零--这种现象叫超导现象。能够发生超导现象的物体叫超导体。材料由正常状态转变为超导状态的温度叫超导材料的转变温度T_C。我国科学家在1989年把T_C提高到130K。现在科学家们正努力做到室温超导。

注意：公式R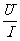＝是电阻的定义式，而R=ρ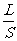是电阻的决定式R与U成正比或R与I成反比的说法是错误的，导体的电阻大小由长度、截面积及材料决定，一旦导体给定，即使它两端的电压U＝0，它的电阻仍然照旧存在。

1.电流

电流的定义式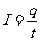：，适用于任何电荷的定向移动形成的电流。

对于金属导体有I=nqvS(n为单位体积内的自由电子个数，S为导线的横截面积，v为自由电子的定向移动速率，约10 ^-5m/s，远小于电子热运动的平均速率10⁵m/s，更小于电场的传播速率3×10⁸m/s)，这个公式只适用于金属导体，千万不要到处套用。

注意：在电解液导电时，是正负离子向相反方向定向移动形成电流，在用公式I＝q／t计算电流强度时应引起注意。

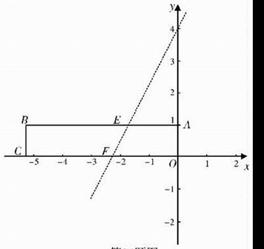
24．(本小题满分14分)如图，在平面直角坐标系中放置一矩形ABCO，其顶点为A(0，1)、B(－3，1)、C(－3，0)、O(0，0)．将此矩形沿着过E(－，1)、F(－，0)的直线EF向右下方翻折，B、C的对应点分别为B′、C′．

(1)求折痕所在直线EF的解析式；

(2)一抛物线经过B、E、B′三点，求此二次函数解析式；

(3)能否在直线EF上求一点P，使得△PBC周长最小？如能，求出点P的坐标；若不能，说明理由．

解：

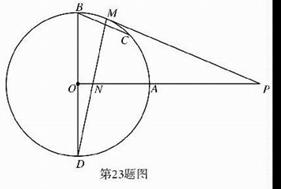
23．(本小题满分12分)

如图，BD是⊙O的直径，OA⊥OB，M是劣弧AB上一点，过点M点作⊙O的切线MP交OA的延长线于P点，MD与OA交于N点．

(1)求证：PM＝PN；

(2)若BD＝4，PA＝ AO，过点B作BC∥MP交⊙O于C点，求BC的长．

(1)证明：

(2)解：

22．(本小题满分8分)“端午”节前，第一次爸爸去超市购买了大小、质量都相同的火腿粽子和豆沙粽子若干，放入不透明的盒中，此时随机取出火腿粽子的概率为；妈妈发现小亮喜欢吃的火腿粽子偏少，第二次妈妈又去买了同样的5只火腿粽子和1只豆沙粽子放入同一盒中，这时随机取出火腿粽子的概率为．

(1)请计算出第一次爸爸买的火腿粽子和豆沙粽子各有多少只？

(2)若妈妈从盒中取出火腿粽子4只、豆沙粽子6只送爷爷和奶奶后，再让小亮从盒中不放回地任取2只，问恰有火腿粽子、豆沙粽子各1只的概率是多少？(用字母和数字表示豆沙粽子和火腿粽子，用列表法计算)

解：

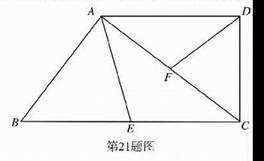
21．(本小题满分8分)如图，直角梯形ABCD中，∠ADC＝90°，AD∥BC，点E在BC上，点F在AC上，∠DFC＝∠AEB．

(1)求证：△ADF ∽△CAE；

(2)当AD＝8，DC＝6，点E、F分别是BC、AC的中点时，求直角梯形ABCD的面积

(1)证明：

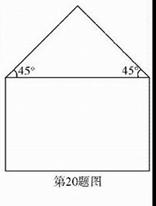
20．(本小题满分8分)用长度为20m的金属材料制成如图所示的金属框，下部为矩形，上部为等腰直角三角形，其斜边长为2x m．当该金属框围成的图形面积最大时，图形中矩形的相邻两边长各为多少？请求出金属框围成的图形的最大面积．

解：

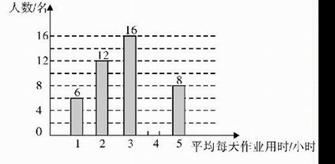
19．(本小题满分8分)某中学生为调查本校学生平均每天完成作业所用时间的情况，随机调查了50名同学，下图是根据调查所得数据绘制的统计图的一部分．

请根据以上信息，解答下列问题：

(1)将统计图补充完整；

(2)若该校共有1800名学生，根据以上调查结果估计该校全体学生每天完成作业所用总时间．

解：

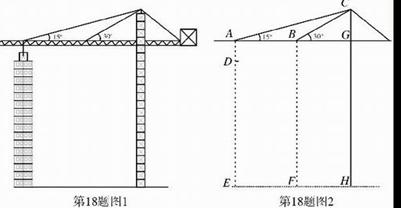
18．(本小题满分8分)图1为已建设封项的16层楼房和其塔吊图，图2为其示意图，吊臂AB与地面EH平行，测得A点到楼顶D点的距离为5m，每层楼高3.5m，AE、BF、CH都垂直于地面，EF＝16cm，求塔吊的高CH的长．

解：