
19.  答案:(
答案:( 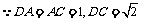 ,
,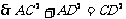 ,
,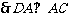 . …3分
. …3分
又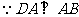 ,
,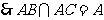
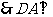 平面
平面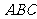 . 6分
. 6分
(II)方法一:取AB中点M,连CM,过M作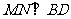 交BD于N,连CN.
交BD于N,连CN.
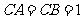 ,
,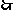
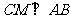 ,
,
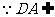 平面
平面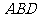 ,
,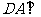 平面
平面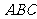 ,
,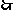 平面
平面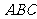
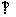 平面
平面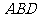 . ………8分
. ………8分
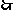
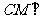 平面
平面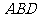 ,
,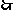
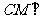
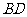 .又
.又

 ,
,
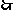
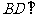 平面
平面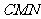 ,
,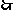

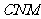 为二面角
为二面角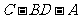 的平面角.…10分
的平面角.…10分
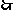
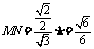 ,
,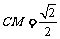 ,
,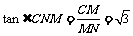 ,
,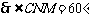 ,
,
故二面角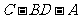 平面角的度数为
平面角的度数为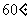 . …………12分
. …………12分
方法二:取AB中点M,连CM.∵AC=AB=1, ∴CM⊥AB.
又∵平面ABC⊥平面ABD,∴CM⊥平面ABD. 取BD中点H,∴MH∥AD.
∵AD⊥AB, ∴MH⊥AB.
分别以AB,MH,MC为x,y,z轴建立空间直角坐标系. …………6分
得 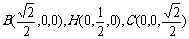 ,
,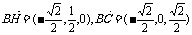 . 8分
. 8分
 设平面BCD的法向量为
设平面BCD的法向量为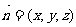
∴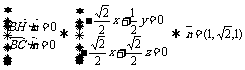 . 10分
. 10分
又∵平面ABD的法向量为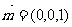 ,
,
∴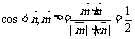 显然二面角
显然二面角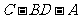 为锐角,所以它的大小为
为锐角,所以它的大小为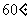 .12分
.12分
20解:(Ⅰ)由题意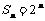 ,
, 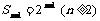 ,两式相减得
,两式相减得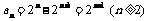 .3分
.3分
当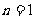 时,
时,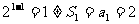 ,∴
,∴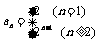 .
-------4分
.
-------4分
(Ⅱ)∵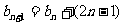 ,∴
,∴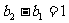 ,
, 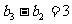 ,
,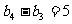 ,………
,………
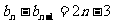 .以上各式相加得
.以上各式相加得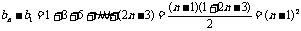 .
.
∵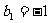 ,∴
,∴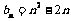 . ---
-6分∴
. ---
-6分∴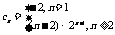 .
-----7分
.
-----7分
∴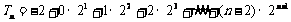 ,
,
∴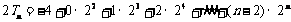 .
.
∴ .
. 
=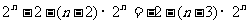 . ∴
. ∴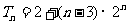 . ----------9分
. ----------9分
(3)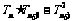 =
=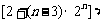
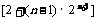
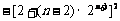
=4+

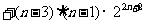
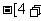
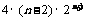
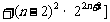 =
=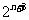
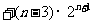
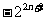
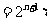
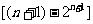 . ∵
. ∵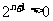 , ∴ 需证明
, ∴ 需证明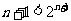 ,用数学归纳法证明如下:
,用数学归纳法证明如下:
①当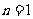 时,
时,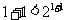 成立 ②假设
成立 ②假设 时,命题成立即
时,命题成立即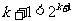 ,
,
那么,当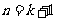 时,
时,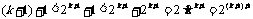 成立.
成立.
由①、②可得,对于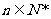 都有
都有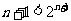 成立.
成立.
∴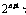
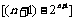
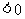 . ∴
. ∴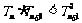 .---12分
.---12分
18.解:(1) 设从甲、乙、丙三台机床加工的零件中任取一件是一等品为事件A,B,C , 则 P(A)=0.7, P(B)=0.6, P(C)=0.8
从甲、乙、丙加工的零件中各取一件检验,至少有一件一等品的概率为
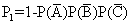 =1-0.3×0.4×0.2=0.976
4分
=1-0.3×0.4×0.2=0.976
4分
(2) 将三台机床加工的零件混合到一起,从中任意的抽取一件检验,它是一等品的概率为 P2=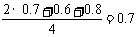 8分
8分
(3) P(X=4)=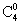 ×0.74=0.2401,
P(X=3)=
×0.74=0.2401,
P(X=3)=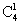 ×0.3×0.73=0.4116
×0.3×0.73=0.4116
P(X=2)=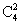 ×0.32×0.72=0.2646, P(X=1)=
×0.32×0.72=0.2646, P(X=1)=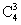 ×0.33×0.7=0.0756
×0.33×0.7=0.0756
P(X=0)=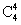 ×0.34=0.0081
×0.34=0.0081
|
X |
4 |
3 |
2 |
1 |
0 |
|
P |
0.2401 |
0.4116 |
0.2646 |
0.0756 |
0.0081 |
X~B(4,0.7),所以EX=4×0.7=2.8 12分
17.解:(1)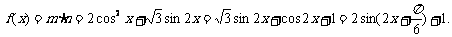
 ---------------2分
---------------2分
令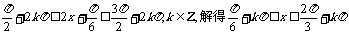
 --------------4分
--------------4分
(2)由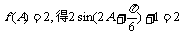 ,
,
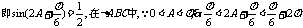
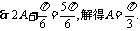 -6分
-6分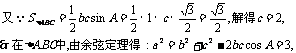
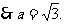 ---------8
---------8
由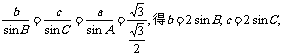
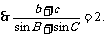 --10分
--10分
22.设函数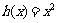 ,
,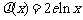 (
(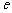 为自然对数的底).
为自然对数的底).
⑴ 求函数 的极值;
的极值;
⑵ 若存在常数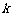 和
和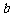 ,使得函数
,使得函数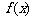 和
和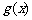 对其定义域内的任意实数
对其定义域内的任意实数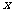 分别满足
分别满足
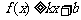 和
和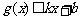 ,则称直线
,则称直线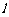 :
: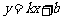 为函数
为函数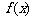 和
和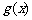 的“隔
的“隔
离直线”.试问:函数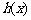 和
和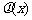 是否存在“隔离直线”?若存在,求出“隔
是否存在“隔离直线”?若存在,求出“隔
 离直线”方程;若不存在,请说明理由.
离直线”方程;若不存在,请说明理由.
保定一中2009-2010届高三数学试卷(理)
21.设椭圆M: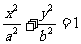 (a>b>0)的离心率为
(a>b>0)的离心率为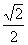 ,长轴长为
,长轴长为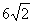 ,设过右焦点F倾斜角为
,设过右焦点F倾斜角为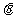 的直线交椭圆M于A,B两点。
的直线交椭圆M于A,B两点。
(Ⅰ)求椭圆M的方程;
(2)设过右焦点F且与直线AB垂直的直线交椭圆M于C,D,求|AB| + |CD|的最小值。
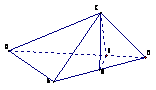
19.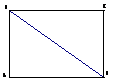
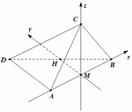
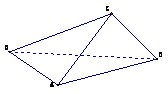 (本小题满分12分)已知矩形ABCD中,
(本小题满分12分)已知矩形ABCD中,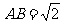 ,
,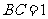 ,现沿对角线
,现沿对角线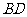 折成二面角
折成二面角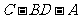 ,使
,使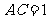 (如图).
(如图).
(I)求证: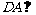 面
面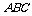 ;
;
(II)求二面角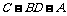 平面角的大小.
平面角的大小.
20(本小题满分12分)
若数列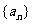 的前
的前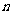 项和
项和 是
是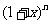 二项展开式中各项系数的和
二项展开式中各项系数的和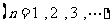 .
.
(Ⅰ)求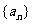 的通项公式;
的通项公式;
(Ⅱ)若数列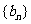 满足
满足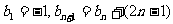 ,且
,且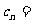
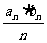 ,求数列
,求数列 的通项及其前
的通项及其前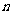 项和
项和 ;
;
(III)求证: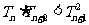 .
.
18.甲、乙、丙三台机床各自独立的加工同一种零件,已知甲、乙、丙三台机床加工的零件是一等品的概率分别为0.7、0.6、0.8,乙、丙两台机床加工的零件数相等,甲机床加工的零件数是乙机床加工的零件数的二倍.
(1)从甲、乙、丙加工的零件中各取一件检验,求至少有一件一等品的概率;
(2)将三台机床加工的零件混合到一起,从中任意的抽取一件检验,求它是一等品的概率;
(3)将三台机床加工的零件混合到一起,从中任意的抽取4件检验,其中一等品的个数记为X,求EX.
17.(本小题满分12分)
设函数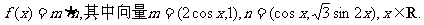
(1)求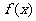 的最小正周期与单调递减区间;
的最小正周期与单调递减区间;
(2)在△ABC中,a、b、c分别是角A、B、C的对边,已知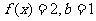 ,△ABC的面积为
,△ABC的面积为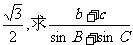 的值。
的值。
16. 在平面直角坐标系中,横坐标、纵坐标均为整数的点称为整点,如果函数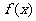 的图象恰好通过
的图象恰好通过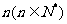 个整点,则称函数
个整点,则称函数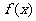 为
为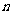 阶整点函数。有下列函数:
阶整点函数。有下列函数:
①
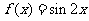 ;
②
;
②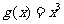 ③
③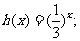 ④
④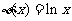 ,
,
其中是一阶整点函数的是________________________________.
三解答题(本大题共6题,共74分,解答应写出文字说明,证明过程或演算步骤。)
15.化简 的结果是____.
的结果是____.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com