
2.计算2x3·x2的结果是()
A.2x B.2x5 C.2x6 D.x5
1.3的倒数是()
A. B.- C.3 D.-3
22. (本小题共12分)
(普通高中做)
如图, 在直三棱柱ABC-A1B1C1中,AC=3,BC=4,AA1=4,点D是AB的中点,
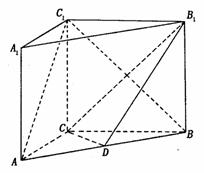 (I)求证:AC⊥BC1;
(I)求证:AC⊥BC1;
(II)求证:AC 1//平面CDB1;
(III)求异面直线 AC1与 B1C所成角的余弦值.
(示范性高中做)
已知正方体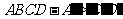 的棱长为1,点
的棱长为1,点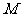 是棱
是棱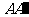 的中点,点
的中点,点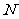 是棱
是棱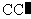 的中点,点
的中点,点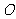 是上底面
是上底面 的中心.
的中心.
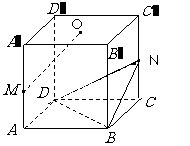 (Ⅰ)求证:MO∥平面NBD;
(Ⅰ)求证:MO∥平面NBD;
(Ⅱ)求二面角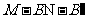 的大小;
的大小;
(Ⅲ)求三棱锥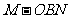 的体积.
的体积.
21.(本小题满分12分)
(文科做)
某商场进行促销活动,促销方案是:顾客每消费100元,便可以获得奖券一张,每张奖券中奖的概率为 ,若中奖,则商场返还顾客现金100元某顾客购买价格为340元的商品,得到3张奖券
,若中奖,则商场返还顾客现金100元某顾客购买价格为340元的商品,得到3张奖券
(I)求商场恰好返还该顾客现金100元的概率;
(II)求商场至少返还该顾客现金100元的概率.
(理科做)
甲、乙两队进行一场排球比赛.根据以往经验,单局比赛甲队胜乙队的概率为0.6,本场比赛采用五局三胜制,即先胜三局的队获胜,比赛结束.设各局比赛相互间没有影响.令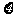 为本场比赛的局数.求
为本场比赛的局数.求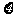 的概率分布和数学期望.(精确到0.0001)
的概率分布和数学期望.(精确到0.0001)
20.(本小题满分12分)
设进入某商场的每一位顾客购买甲种商品的概率是0.5,购买乙种商品的概率是0.6,且购买甲种商品和购买乙种商品是相互独立的,各顾客之间购买商品也是互相独立的.
(Ⅰ)求进入商场的1位顾客购买甲、乙两种商品中的一种的概率;
(Ⅱ)求进入商场的1位顾客至少购买甲、乙两种商品中的一种的概率.
19.(本小题满分12分)
书桌上一共有六本不同的书.问:
(Ⅰ)6本书排成一排,要求其中的2本数学书排在一起,共有多少种不同的排法?
(Ⅱ)6本书分给甲、乙、丙三个同学,每人2本,共有多少种不同方法?
(Ⅲ)(示范性高中做)6本书分给甲、乙、丙三个同学,如果一个人得1本,一个人得2本,一个人得3本,共有多少种不同的分法?
18. ( 本小题满分12分)
( 本小题满分12分)
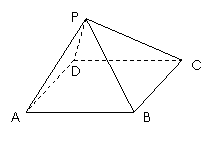
(普通中学做)如图,四棱锥P-ABCD中,底面ABCD 为矩形,AB=8,AD=4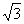 ,侧面PAD为等边三角形,并且与底面所成二面角为60°.
,侧面PAD为等边三角形,并且与底面所成二面角为60°.
求PA与底面ABCD所成角的大小.
(示范性高中做)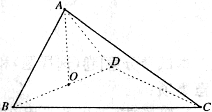 如图,四面体
如图,四面体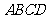 中,
中,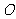 是
是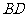 的中点,
的中点,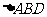 和
和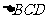 均为等边三角形,
均为等边三角形,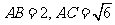 .
.
(I)求证: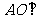 平面
平面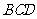 ;
;
(Ⅱ)求二面角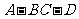 的余弦值.
的余弦值.
17.(本小题满分10分)
已知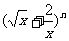 的展开式中第五项的系数与第三项的系数之比是10︰1,求展开式中x的系数.
的展开式中第五项的系数与第三项的系数之比是10︰1,求展开式中x的系数.
16. 从1,2,…,9这九个数中,随机抽取3个不同的数,则这3个数的和为偶数的概率是
.
15. 把正方形ABCD沿对角线AC折起,当A、B C、D四点为顶点的三棱锥体积最大时,直线BD与平面ABC所成的角的大小为 ;
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com