20.(本小题满分12分)

已知a是实数，函数f (x) = x²(x - a).

(1) 若f ′ (1) = 3，求a的值及曲线y = f (x)在点(1 , f (1))处的切线方程；

(2) 求f (x)在区间[0 , 2]上的最大值.

19.(本小题满分12分)

如图所示，在菱形ABCD中，∠DAB = 60°，PA⊥底面ABCD，PA = AB = 2，E、F分别是AB与PD的中点.

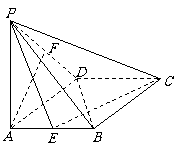(1) 求证：PC⊥BD；

(2) 求证：AF∥平面PEC；

(3) 求二面角P - EC - D的大小.

18. (本小题满分12分)

甲、乙两个小孩进行抛掷塑料圈套玩具的游戏，他们套中与否相互独立.游戏规则如下：若某小孩抛掷一次套中玩具，则由该小孩继续抛掷；若抛掷一次没有套中，就由另一个小孩接

替抛掷.已知甲、乙两个小孩每抛掷一次套中的概率均为，且第1次由甲开始抛掷.

(1) 求前3次抛掷塑料套圈，甲恰好套中2次的概率；

(2) 第4次由甲抛掷的概率.

17.(本小题满分12分)

已知f (x) = 2cos² x + 2sin xcos x + a (a为常数).

(1) 求f (x)的单调递增区间；

(2) 若f (x)在区间[ - , ]上的最大值与最小值之和为3，求a的值.

16.在△ABC中，给出下列命题：

①若sin 2A = sin 2B，则△ABC是等腰三角形；

②若sin A = cos B，则△ABC是直角三角形；

③若cos Acos Bcos C < 0，则△ABC是钝角三角形；

④若cos (A - B)cos (B - C)cos (C - A) = 1，则△ABC是等边三角形；

　 其中正确的命题有 　　　　(写出所有真命题的序号).

15.已知双曲线 - = 1 (a , b∈R⁺)的离心率e∈[ , 2 ]，则一条渐近线与实轴所构成角的

取值范围是 　　　　.

14.国家修建经济适用房以解决低收入家庭住房紧张问题.统计数据表示，甲、乙、丙三个社区现分别有低收入家庭180户、150户、90户，若第一批经济适用房中有70套用于解决这三个社区中70户低收入家庭的住房问题.现采用分层抽样的方法决定各社区的户数，则应从甲社区中抽取低收入家庭的户数为 　　　　.

13.若向量a = (t , t + )，b = (- t , 2)，且a与b的夹角小于90°，则t的取值范围是　　　　 .

12.已知抛物线x² = 2py (p > 0)，过点M (0 , - )向抛物线引两条切线，A、B为切点，则线段

AB的长度是

第Ⅱ卷

11.已知过点P ( , 0)的直线l交圆O：x² + y² = 1于A、B两点，且 = 2，则△AOB的面积为