
8. 在相同条件下,下列说法错误的是
A.氯气在饱和食盐水中的溶解度小于在纯水中的溶解度
B.碘在碘化钾溶液中的溶解度大于在纯水中的溶解度
C.醋酸在醋酸钠溶液中电离的程度大于在纯水中电离的程度
D.工业上生产硫酸的过程中使用过量的空气可提高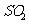 的利用率
的利用率
7. 下面均是正丁烷与氧气反应的热化学方程式(25°,101kPa):
① 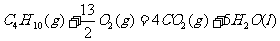
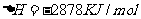
②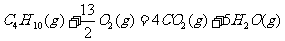
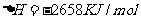
③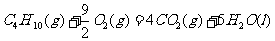
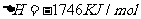
④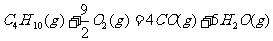
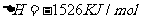
由此判断,正丁烷的燃烧热是
A.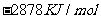 B.
B. 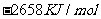 C.
C.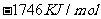 D.
D.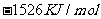
6. 下列反应中,可用离子方程式 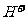 +
+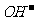 =
=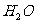 表示的是
表示的是
A. 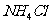 +
+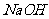

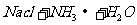
B.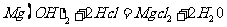
C.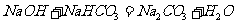
D. 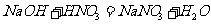
5. 下列叙述符合基因工程概念的是
A.B淋巴细胞与肿瘤细胞融合,杂交瘤细胞中含有B淋巴细胞中的抗体基因
B.将人的干扰素基因重组到质粒后导入大肠杆菌,获得能产生人干扰素的菌株
C.用紫外线照射青霉菌,使其DNA发生改变,通过筛选获得青霉素高产菌株
D.自然界中天然存在的噬菌体自行 感染细菌后其DNA整合到细菌DNA上
感染细菌后其DNA整合到细菌DNA上
4. 已知某环境条件下某种动物的AA和Aa个体全部存活,aa个体在出生前会全部死亡。现有该动物的一个大群体,只有AA、Aa两种基因型,其比例为1:2.假设每对亲本只交配一次且成功受孕,均为单胎。在上述环境条件下,理论上该群体随机交配产生的第一代中AA和Aa的比例是
A.1:1 B. 1:2 C. 2:1 D. 3:1
3. 下列关于生态系统的叙述,错误的是
A. 草原生态系统比农田生态系统的群落结构复杂
B. 环境条件分布不均匀是形成群落水平结构的原因之一
C. 我国南方热带雨林中分解者的代谢活动比北方森林中的弱
D. 植物可通过呼吸作用和光合作用参与生态系统的碳循环
2. 下列关于免疫细胞的叙述,错误的是
A. 效应T细胞可以释放淋巴因子
B. T淋巴细胞可以产生多种抗体
C. 吞噬细胞和淋巴细胞均属于免疫细胞
D. 一个效应B淋巴细胞只能产生一种抗体
1. 下列关于高尔基体的叙述,错误的是
A. 高尔基体膜具有流动性
B. 抗体从合成到分泌不经过高尔基体
C. 高尔基体膜主要由磷脂和蛋白质构成
D. 高尔基体具有对蛋白质进行加工的功能
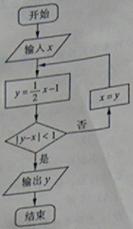
(13)执行右图所示的程序框图,若输入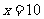 ,则输出
,则输出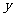 的值为
.
的值为
.
[答案]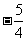
[解析]当x=10时,y=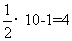 ,此时|y-x|=6;
,此时|y-x|=6;
当x=4时,y=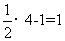 ,此时|y-x|=3;当x=1时,y=
,此时|y-x|=3;当x=1时,y=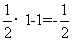 ,此时|y-x|=
,此时|y-x|=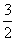 ;
;
当x=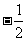 时,y=
时,y=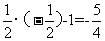 ,此时|y-x|=
,此时|y-x|=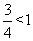 ,故输出y的值为
,故输出y的值为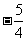 。
。
[命题意图]本题考查程序框图的基础知识,考查了同学们的试图能力。
 [答案]
[答案]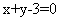
[解析]由题意,设所求的直线方程为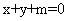 ,设圆心坐标为
,设圆心坐标为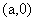 ,则由题意知:
,则由题意知:
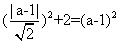 ,解得
,解得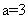 或-1,又因为圆心在x轴的正半轴上,所以
或-1,又因为圆心在x轴的正半轴上,所以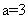 ,故圆心坐标为
,故圆心坐标为
(3,0),因为圆心(3,0)在所求的直线上,所以有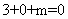 ,即
,即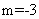 ,故所求的直线方程为
,故所求的直线方程为
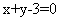 。
。
[命题意图]本题考查了直线的方程、 点到直线的距离、直线与圆的关系,考查了同学们解决直线与圆问题的能力。
点到直线的距离、直线与圆的关系,考查了同学们解决直线与圆问题的能力。
 (18)(本小题满分12分)
(18)(本小题满分12分)
已知等差数列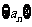 满足:
满足: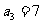 ,
,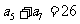 ,
,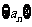 的前n项和为
的前n项和为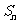 .
.
(Ⅰ)求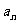 及
及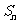 ;
;
(Ⅱ)令bn=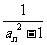 (n
(n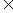 N*),求数列
N*),求数列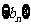 的前n项和
的前n项和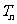
 .
.
[解析](Ⅰ)设等差数列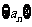 的公差为d,因为
的公差为d,因为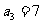 ,
,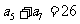 ,所以有
,所以有
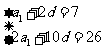 ,解得
,解得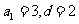 ,
,
所以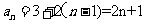 ;
;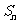 =
=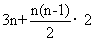 =
=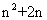 。
。
(Ⅱ)由(Ⅰ)知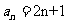 ,所以bn=
,所以bn=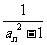 =
=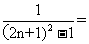
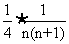 =
= ,
,
所以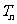 =
=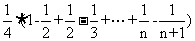 =
=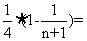
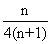 ,
,
即数列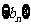 的前n项和
的前n项和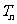 =
=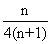 。
。
[命题意图]本题考查等差数列的通项公式与前n项和公式的应用、裂项法求数列的和,熟练数列的基础知识是解答好本类题目的关键。
 (19)(本小题满分12分)
(19)(本小题满分12分)
如图,在五棱锥P-ABCDE中,PA⊥平面ABCDE,AB∥CD,AC∥ED,AE∥BC,  ABC=45°,AB=2
ABC=45°,AB=2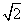 ,BC=2AE=4,三角形PAB是等腰三角形.
,BC=2AE=4,三角形PAB是等腰三角形.
(Ⅰ)求证 :平面PCD⊥平面PAC;
:平面PCD⊥平面PAC;
(Ⅱ)求直线PB与 平面PCD所成角的大小;
平面PCD所成角的大小;
(Ⅲ)求四棱锥 P-ACDE的体积.
P-ACDE的体积.
[解析](Ⅰ)证明:因为 ABC=45°,AB=2
ABC=45°,AB=2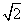 ,BC=4,所以在
,BC=4,所以在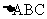 中,由余弦定理得:
中,由余弦定理得: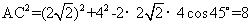 ,解得
,解得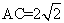 ,
,
所以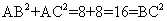 ,即
,即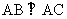 ,又PA⊥平面ABCDE,所以PA⊥
,又PA⊥平面ABCDE,所以PA⊥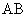 ,
,
又PA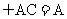 ,所以
,所以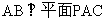 ,又AB∥CD,所以
,又AB∥CD,所以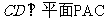 ,又因为
,又因为
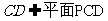 ,所以平面PCD⊥平面PAC;
,所以平面PCD⊥平面PAC;
(Ⅱ)由(Ⅰ)知平面PCD⊥平面PAC,所以在平面PAC内,过点A作 于H,则
于H,则
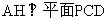 ,又AB∥CD,AB
,又AB∥CD,AB 平面
平面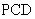 内,所以AB平行于平面
内,所以AB平行于平面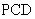 ,所以点A到平面
,所以点A到平面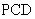 的距离等于点B到平面
的距离等于点B到平面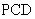 的距离,过点B作BO⊥平面
的距离,过点B作BO⊥平面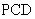 于点O,则
于点O,则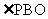 为所求角,且
为所求角,且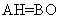 ,又容易求得
,又容易求得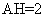 ,所以
,所以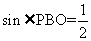 ,即
,即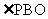 =
=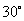 ,所以直线PB与平面PCD所成角的大小为
,所以直线PB与平面PCD所成角的大小为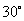 ;
;
(Ⅲ)由(Ⅰ)知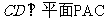 ,所以
,所以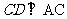 ,又AC∥ED,所以四边形ACDE是直角梯形,又容易求得
,又AC∥ED,所以四边形ACDE是直角梯形,又容易求得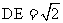 ,AC=
,AC=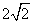 ,所以四边形ACDE的面积为
,所以四边形ACDE的面积为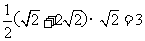 ,所以
,所以
四棱锥 P-ACDE的体积为
P-ACDE的体积为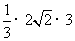 =
=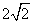 。
。


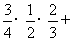
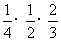
 =
=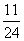 ,
,
所以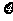 的分布列为
的分布列为
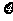 |
2 |
3 |
4 |
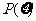 |
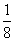 |
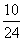 |
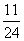 |
数学期望 =
=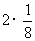 +
+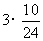 +4
+4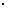
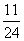 =
=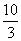 。
。
[命题意图]本题考查了相互独立事件同时发生的概率、考查了离散型随机变量的分布列以及数学期望的知识,考查了同学们利用所学知识解决实际问题的能力。
(21)(本小题满分12分)
如图,已知椭圆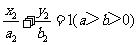 的离心率为
的离心率为 ,以该椭圆上的点和椭圆的左、右焦点
,以该椭圆上的点和椭圆的左、右焦点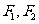 为顶点的三角形
为顶点的三角形 的周长为
的周长为
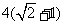 .一等轴双曲线的顶
.一等轴双曲线的顶 点是该椭圆的焦点,设
点是该椭圆的焦点,设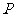 为该双曲线上异于顶点的任一点,直线
为该双曲线上异于顶点的任一点,直线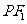 和
和 与椭圆的交点分别为
与椭圆的交点分别为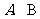 和
和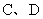 .
.
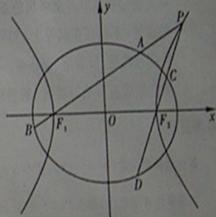
(Ⅰ)求椭圆和双曲线的标准方程;
(Ⅱ)设直线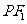 、
、 的斜率分别为
的斜率分别为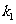 、
、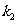 ,证明
,证明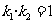 ;
;
(Ⅲ)是否存在常数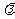 ,使得
,使得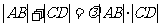 恒成立
恒成立 ?若存在,求
?若存在,求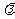 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
[解析](Ⅰ)由题意知,椭圆离心率为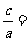
 ,得
,得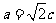 ,又
,又
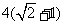 ,所以可解得
,所以可解得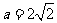 ,
,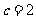 ,所以
,所以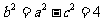 ,所以椭圆的标准方程为
,所以椭圆的标准方程为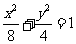 ;所以椭圆的焦点坐标为(
;所以椭圆的焦点坐标为( ,0),因为双曲线为等轴双曲线,且顶
,0),因为双曲线为等轴双曲线,且顶 点是该椭圆的焦点,所以该双曲线的标准方程为
点是该椭圆的焦点,所以该双曲线的标准方程为
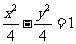 。
。
 [命题意图]本题考查了椭圆的定义、离心率、椭圆与双曲线的标准方程、直线与圆锥曲线的位置关系,是一道综合性的试题,考查了学生综合运用知识解决问题的能力。其中问题(3)是一个开放性问题,考查了同学们观察、推理以及创造性地分析问题、解决问题的能力,
[命题意图]本题考查了椭圆的定义、离心率、椭圆与双曲线的标准方程、直线与圆锥曲线的位置关系,是一道综合性的试题,考查了学生综合运用知识解决问题的能力。其中问题(3)是一个开放性问题,考查了同学们观察、推理以及创造性地分析问题、解决问题的能力,
(22)(本小题满分14分)
已知函数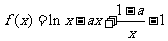
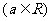 .
.
(Ⅰ)当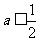 时,讨论
时,讨论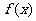 的单调性;
的单调性;
(Ⅱ)设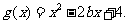 当
当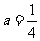 时,若对任意
时,若对任意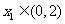 ,存在
,存在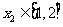 ,使
,使
 ,求实数
,求实数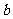 取值范围.
取值范围.
 (Ⅱ)当
(Ⅱ)当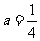 时,
时,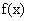 在(0,1)上是减函数,在(1,2)上是增函数,所以对任意
在(0,1)上是减函数,在(1,2)上是增函数,所以对任意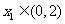 ,
,
有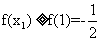 ,又已知存在
,又已知存在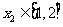 ,使
,使 ,所以
,所以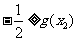 ,
,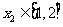 ,
,
即存在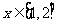 ,使
,使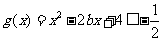 ,即
,即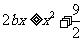 ,即
,即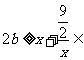
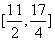 ,
,
所以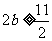 ,解得
,解得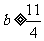 ,即实数
,即实数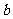 取值范围是
取值范围是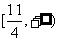 。
。
[命题意图]本题将导数、二次函数、不等式知识有机的 结合在一起,考查了利用导数研究函数的单调性、利用导数求函数的最值以及二次函数的最值问题,考查了
结合在一起,考查了利用导数研究函数的单调性、利用导数求函数的最值以及二次函数的最值问题,考查了 同学们分类讨论的数学思想以及解不等式的能力;考查了学生综合运用所学知识分析问题、解决问题的能力。
同学们分类讨论的数学思想以及解不等式的能力;考查了学生综合运用所学知识分析问题、解决问题的能力。
(1)直接利用函数与导数的关系讨论函数的单调性;(2)利用导数求出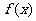 的最小值、利用二
的最小值、利用二 次函数知识或分离常数法求出
次函数知识或分离常数法求出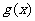 在闭区间[1,2]上的最大值,然后解不等式求参数。
在闭区间[1,2]上的最大值,然后解不等式求参数。
有一项是满足题目要求的.
(1)
已知全集U=R,集合M={x||x-1| 2},则
2},则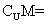
(A){x|-1<x<3} (B){x|-1 x
x 3} (C){x|x<-1或x>3} (D){x|x
3} (C){x|x<-1或x>3} (D){x|x -1或x
-1或x 3}
3}
[答案]C
[解析]因为集合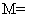
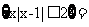
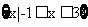 ,全集
,全集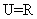 ,所以
,所以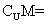
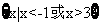 ,故选C.
,故选C.
[命题意图]本题考查集合的补集运算,属容易题.
(2)
已知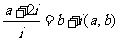
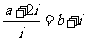 (a,b∈R),其中i为虚数单位,则a+b=
(a,b∈R),其中i为虚数单位,则a+b=
(A)-1 (B)1 (C)2 (D)3
[答案]B
[解析]由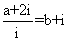 得
得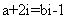 ,所以由复数相等的意义知:
,所以由复数相等的意义知: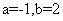 ,所以
,所以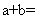 1,故选B.
1,故选B.
[命题意图]本题考查复数相等的意义、复数的基本运算,属保分题。
(3)在空间,下列命题正确的是
(A)平行直线的平行投影重合
( B)平行于同一直线的两个平面平行
B)平行于同一直线的两个平面平行
(C)垂直于同一平面的两个平面平行
(D)垂直于同一 平面的两条直线平行
平面的两条直线平行
[答案]D
[解析]由空间直线与平面的位置关系及线面垂直与平行的判定与性质定理可以很容易得出答案。
[命题意图]本题考查空间直线与平面的位置关系及线面垂直与平行的判定与性质,属基础题。
(4)设f(x)为定义在R上的奇函数,当x≥0时,f(x)=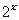 +2x+b(b为常数),则f(-1)=
+2x+b(b为常数),则f(-1)=
(A) 3 (B) 1 (C)-1 (D)-3
[答案]D
 (7)由曲线y=
(7)由曲线y=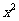 ,y=
,y= 围成的封闭图形面积为
围成的封闭图形面积为
(A)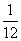 (B)
(B)
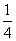 (C)
(C) 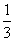 (D)
(D)
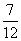
[答案]A
[解析]由题意得:所求封闭图形的面积为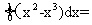
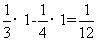 ,故选A。
,故选A。
[命题意图]本题考查定积分的基础知识,由定积分求曲线围成封闭图形的面积。
(8)某台小型晚会由6个节目组成,演出顺序有如下要求:节目甲必须排在第四位、节目乙不能排在第一位,节目丙必须排在最后一位,该台晚会节目演出顺序的编排方案共有
 (A)36种 (B)42种 (C)48种 (D)54种
(A)36种 (B)42种 (C)48种 (D)54种
[答案]B
 可知当直线
可知当直线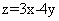 平移到点(5,3)时,目标函数
平移到点(5,3)时,目标函数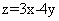 取得最大值3;当直线
取得最大值3;当直线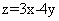 平移到点(3,5)时,目标函数
平移到点(3,5)时,目标函数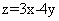 取得最小值-11,故选A。
取得最小值-11,故选A。
[命题意图]本题考查不等式中的线性规划知识,画出平面区域与正确理解目标函数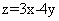 的几何意义是解答好本题的关键。
的几何意义是解答好本题的关键。
(1 1)函数y=2x
1)函数y=2x  -
-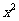 的图像大致是
的图像大致是
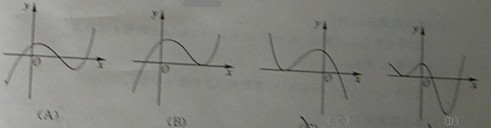
[答案]A
[解析]因为当x=2或4时,2x  -
-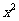 =0,所以排除B、C;当x=-2时,2x
=0,所以排除B、C;当x=-2时,2x  -
-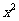 =
=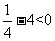 ,故排除D,所以选A。
,故排除D,所以选A。
[命题意图]本题考查函数的图象,考查同学们对函数基础知识的把握程度以及数形结合的思维能力。
(12)定义平面向量之间的一种运算“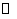 ”如下,对任意的
”如下,对任意的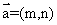 ,
, ,令
,令
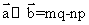 ,下面说法错误的是( )
,下面说法错误的是( )
A.若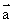 与
与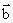 共线,则
共线,则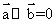 B.
B.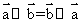
C.对任意的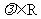 ,有
,有
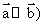 D.
D. 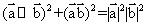
[答案]B
 [解析]若
[解析]若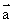 与
与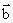 共线,则有
共线,则有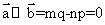 ,故A正确;因为
,故A正确;因为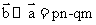 ,而
,而
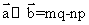 ,所以有
,所以有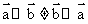 ,故选项B错误,故选B。
,故选项B错误,故选B。
[命题意图]本题在平面向量的基础上,加以创新,属创新题型,考查平面向量的基础知识以及分析问题、解决问题的能力。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com