
4.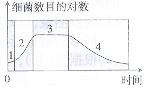 在制备单克隆抗体的过程中,对骨髓瘤细胞和免疫的B淋巴细胞诱导融合后,要用特定培养基筛选出杂交瘤细胞在这种培养基上不能存活和繁殖的细胞有①B淋巴细胞②小鼠骨髓瘤细胞 ③杂交瘤细胞 ④B淋巴细胞自身融合细胞 ⑤小鼠骨髓瘤细胞自身融合细胞
在制备单克隆抗体的过程中,对骨髓瘤细胞和免疫的B淋巴细胞诱导融合后,要用特定培养基筛选出杂交瘤细胞在这种培养基上不能存活和繁殖的细胞有①B淋巴细胞②小鼠骨髓瘤细胞 ③杂交瘤细胞 ④B淋巴细胞自身融合细胞 ⑤小鼠骨髓瘤细胞自身融合细胞
A.①②③ B.①②④⑤ C.①② D.①④
3.下列关于植物个体生殖和发育过程的相关叙述,正确的是( )
A.被子植物受精卵子经过细胞的分裂和分化,形成胚和胚乳
B.在植物的发育过程中均存在细胞的分裂、分化、癌变和衰老
C.被子植物即可以进行有性生殖也可以进行无性生殖
D.输入幼叶的氮、磷、钾、镁均来自老叶,而铁、钙只能从体外吸收
2.线粒体DNA(mtDNA),是指一些位于线粒体内的DNA,结构类似于质粒DNA现今人类体内每个mtDNA(tRNA)与两种核糖体RNA(rRNA)下面相关叙述正确的是( )
A.mtDNA一般和蛋白质结合在一起
B.人体mtDNA可能只控制合成一部分tRNA
C.需氧生物体内都有线粒体的分布
D.人体mtDNA中的基因都用于指导蛋白质的合成
1.在遭到禽流感和甲型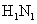 流感侵袭之后,荷兰又爆发一种新型流感--“羊流感”,病原体为原核生物中的贝纳柯克斯体,生活方式也是胞内寄生对于“羊流感”的理解,错误的是( )
流感侵袭之后,荷兰又爆发一种新型流感--“羊流感”,病原体为原核生物中的贝纳柯克斯体,生活方式也是胞内寄生对于“羊流感”的理解,错误的是( )
A.感染“羊流感”后,人体参与免疫的细胞主要是B淋巴细胞
B.引起“羊流感”的贝纳氏柯克斯体培养时需用活细胞培养
C.贝纳氏柯克斯体具有细胞壁、细胞膜、细胞质和拟核等结构
D.贝纳氏柯克斯体在遗传时不遵循孟德尔遗传定律
(17)(本小题满分10分)(注意:在试题卷上作答无效)
在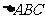 中,内角A、B、C的对边长分别为
中,内角A、B、C的对边长分别为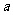 、
、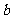 、
、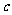 ,已知
,已知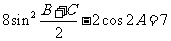 ,且
,且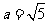 ,
,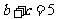 ,求角A及
,求角A及 的面积
的面积
(18)(本小题满分12分)(注意:在试题卷上作答无效)
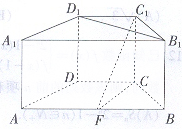 如图,在直四棱柱
如图,在直四棱柱 中,底面
中,底面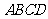 为等腰梯形,
为等腰梯形,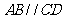 ,
,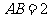 ,
,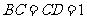 ,
,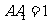 ,
,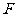 在棱
在棱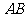 (不含端点)上,且
(不含端点)上,且 与底面
与底面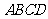 所成角的大小为
所成角的大小为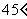
(Ⅰ)证明:直线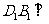 平面
平面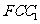 ;
;
(Ⅱ)求二面角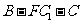 的大小
的大小
(19)(本小题满分12分)(注意:在试题卷上作答无效)
桂林某学校从参加高三年级第二次模拟考试的学生中
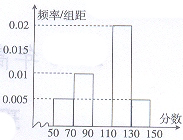 随机抽出100名学生,将其数学成绩(均为整数)分成五
随机抽出100名学生,将其数学成绩(均为整数)分成五
段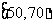 ,
,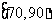 ,
,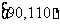 ,
,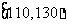 ,
,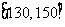
后得到如右部分频率分布直方图,分析图形的信息,回答下
列问题:
(Ⅰ)求分数在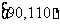 内的频率和学生数,并补全这
内的频率和学生数,并补全这
个频率分布直方图;
(Ⅱ)现从分数段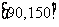 的学生中随机抽取2人给予助学金奖励,抽到的学生成绩在
的学生中随机抽取2人给予助学金奖励,抽到的学生成绩在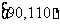 内每人奖励100元,在
内每人奖励100元,在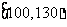 内每人奖励200元,在
内每人奖励200元,在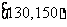 内每人奖励300元,用
内每人奖励300元,用 表示抽取结束后总的奖励金额,求
表示抽取结束后总的奖励金额,求 的分布列和数学期望
的分布列和数学期望
(20)(本小题满分12分)(注意:在试题卷上作答无效)
已知数列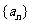 满足
满足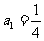 ,
,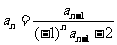 (
(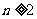 ,
,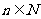 )
)
(Ⅰ)求数列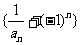 的通项公式;
的通项公式;
(Ⅱ)设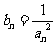 (
(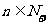 ),求数列
),求数列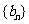 的前
的前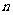 项和
项和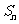
(21)(本小题满分12分)(注意:在试题卷上作答无效)
已知 、
、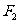 是椭圆
是椭圆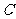 :
: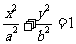 (
(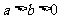 )的左、右焦点,
)的左、右焦点,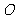 为坐标原点,椭圆上的点到焦点距离的最大值为
为坐标原点,椭圆上的点到焦点距离的最大值为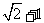 ,最小值为
,最小值为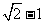
(Ⅰ)求椭圆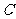 的标准方程;
的标准方程;
(Ⅱ)已知⊙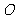 是以
是以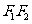 为直径的圆,一直线
为直径的圆,一直线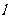 :
: 与⊙
与⊙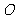 相切,与椭圆
相切,与椭圆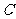 交于不同的两点
交于不同的两点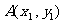 、
、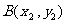 ,且满足
,且满足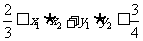 ,求
,求 面积
面积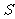 的最大值
的最大值
(22)(本小题满分12分)(注意:在试题卷上作答无效)
已知函数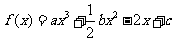 的图象在点
的图象在点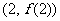 处的切线方程为
处的切线方程为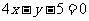 ,且在
,且在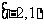 内单调递减,在
内单调递减,在 上单调递增
上单调递增
(Ⅰ)求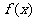 的解析式;
的解析式;
(Ⅱ)若对于任意的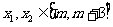 (
(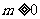 ),不等式
),不等式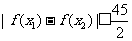 恒成立,试问这样的
恒成立,试问这样的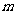 是否存在?若存在,求出
是否存在?若存在,求出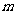 的范围;若不存在,请说明理由
的范围;若不存在,请说明理由
(13)已知双曲线 的一条渐近线方程为
的一条渐近线方程为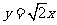 ,则该双曲线的离心率是
,则该双曲线的离心率是
(14)已知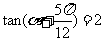 ,则
,则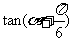 的值为
的值为
(15)若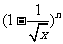 (
(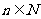 ,
,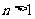 )的展开式中
)的展开式中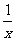 的系数为
的系数为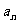 ,
,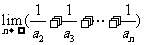 等于
等于
(16)正四棱柱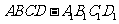 的顶点在同一球面上,且任意两个顶点的球面距离的最大值和最小值分别为
的顶点在同一球面上,且任意两个顶点的球面距离的最大值和最小值分别为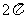 和
和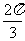 ,则正四棱柱
,则正四棱柱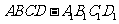 的体积为
的体积为
(1)已知集合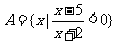 ,
,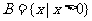 ,那么集合
,那么集合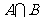 等于( )
等于( )
(A)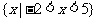 (B)
(B)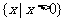
(C) (D)
(D)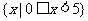
(2)已知复数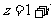 (
(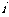 是虚数单位),则
是虚数单位),则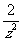
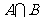 等于( )
等于( )
(A) (B)
(B) (C)
(C)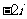 (D)
(D)
(3)在等比数列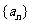 中,若
中,若 和
和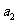 是一元二次方程
是一元二次方程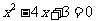 的两个根,则
的两个根,则 等于( )
等于( )
(A)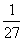 (B)
(B)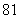 (C)
(C)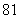 或
或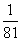 (D)
(D)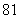 或
或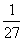
(4)下列所给的有关命题中,说法错误的命题是( )
(A)命题“若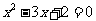 ,则
,则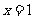 ”的逆否命题是“若
”的逆否命题是“若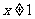 ,则
,则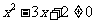 ”
”
(B)“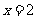 ”是“
”是“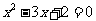 ”的充分不必要条件
”的充分不必要条件
(C)若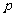 或
或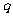 为假命题,则
为假命题,则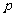 、
、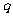 均为假命题
均为假命题
(D)在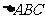 中,若向量
中,若向量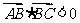 ,则角B为钝角
,则角B为钝角
(5)在正四棱锥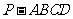 中,
中,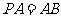 ,
,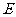 、
、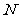 、
、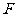 分别为棱
分别为棱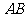 、棱
、棱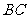 和棱
和棱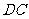 的中点,则异面直线
的中点,则异面直线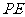 与
与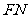 所成角为( )
所成角为( )
(A)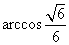 (B)
(B)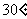 (C)
(C)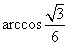 (D)
(D)
(6)将函数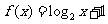 的反函数的图象按向量
的反函数的图象按向量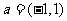 平移后得到函数
平移后得到函数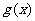 ,则
,则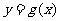 的图象可能为( )
的图象可能为( )

(7)设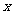 ,
,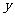 满足约束条件
满足约束条件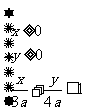 ,若目标函数
,若目标函数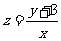 最小值为1,则
最小值为1,则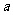 的值为( )
的值为( )
(A)0 (B)1 (C) (D)3
(D)3
(8)2010年上海世博会期间,A、B、C、D四名志愿者分别从事翻译、导游、礼仪、司机四项工作,则A不从事翻译且B不从事导游的不同组合方案有( )
(A)6种 (B)8种 (C)14种 (D)24种
(9)曲线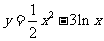 在点
在点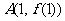 处的切线与坐标轴围成的封闭图形的面积为( )
处的切线与坐标轴围成的封闭图形的面积为( )
(A)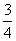 (B)
(B)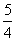 (C)
(C)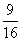 (D)
(D)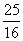
(10)已知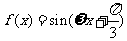 (
( )的图像与
)的图像与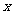 轴两相邻交点间的距离为
轴两相邻交点间的距离为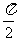 ,要得到
,要得到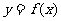 的图像只须把
的图像只须把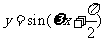 的图像( )
的图像( )
(A)向左平移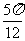 个单位 (B)向右平移
个单位 (B)向右平移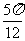 个单位
个单位
(C)向左平移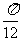 个单位 (D)向右平移
个单位 (D)向右平移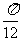 个单位
个单位
(11)已知实数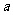 满足方程
满足方程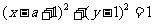 ,当
,当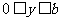 (
(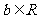 )时,由此方程可以确定一个偶函数
)时,由此方程可以确定一个偶函数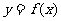 ,则抛物线
,则抛物线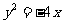 的焦点到动点(
的焦点到动点(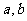 )所构成的轨迹上点的距离的最大值为( )
)所构成的轨迹上点的距离的最大值为( )
(A)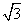 (B)
(B)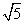 (C)
(C)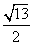 (D)
(D)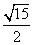
(12)已知函数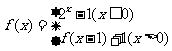 ,把方程
,把方程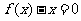 的根按从小到大的顺序排成一个数列,则该数列的前
的根按从小到大的顺序排成一个数列,则该数列的前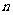 项和为( )
项和为( )
(A)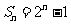 (
(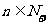 ) (B)
) (B)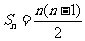 (
(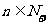 )
)
(C)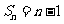 (
(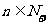 ) (D)
) (D)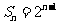 (
(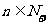 )
)
第Ⅱ卷
(17)(本小题满分10分)(注意:在试题卷上作答无效)
已知数列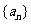 是公比为正数的等比数列,
是公比为正数的等比数列,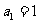 ,且
,且 是
是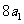 与
与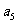 的等差中项,求数理
的等差中项,求数理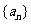 的前
的前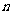 项和
项和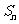
(18)(本小题满分12分)(注意:在试题卷上作答无效)
在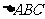 中,内角A、B、C的对边长分别为
中,内角A、B、C的对边长分别为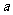 、
、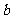 、
、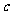 ,已知
,已知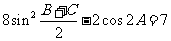 ,且
,且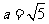 ,
,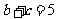 ,求角A及
,求角A及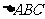 的面积
的面积
(19)(本小题满分12分)(注意:在试题卷上作答无效)
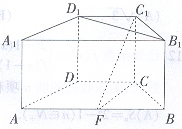 如图,在直四棱柱
如图,在直四棱柱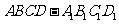 中,底面
中,底面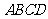 为等腰梯形,
为等腰梯形,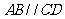 ,
,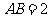 ,
,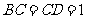 ,
,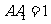 ,
,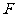 在棱
在棱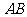 (不含端点)上,且
(不含端点)上,且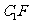 与底面
与底面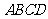 所成角的大小为
所成角的大小为
(Ⅰ)证明:直线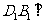 平面
平面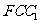 ;
;
(Ⅱ)求二面角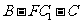 的余弦值
的余弦值
(20)(本小题满分12分)(注意:在试题卷上作答无效)
桂林的“两江四湖”(漓江、桃花江、榕湖、杉湖、桂湖、木龙湖)使桂林“城在景中,景在城中,城景交融”的特点得到了淋漓尽致的展现某旅行社为了吸引游客,宣传桂林,从一艘游船中抽出9人,其中有3名男士和6名女士,进行有奖问答,每次只随机选1人作答,任一个人都可能被多次选中,现只选两次且每次被选中与否互不影响
(Ⅰ)求两次都选中甲的概率;
(Ⅱ)求男士被选中次数不少于女士被选中次数的概率
(21)(本小题满分12分)(注意:在试题卷上作答无效)
已知函数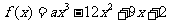 ,若
,若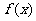 在
在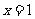 处的切线斜率为
处的切线斜率为
(Ⅰ)求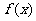 的解析式及单调区间;
的解析式及单调区间;
(Ⅱ)若对任意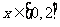 都有
都有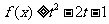 成立,求实数
成立,求实数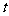 的取值范围
的取值范围
(22)(本小题满分12分)(注意:在试题卷上作答无效)
已知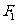 、
、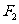 是椭圆
是椭圆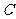 :
: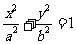 (
(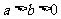 )的左、右焦点,
)的左、右焦点,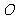 为坐标原点,椭圆上的点到焦点距离的最大值为
为坐标原点,椭圆上的点到焦点距离的最大值为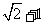 ,最小值为
,最小值为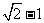
(Ⅰ)求椭圆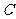 的标准方程;
的标准方程;
(Ⅱ)已知⊙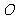 是以
是以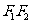 为直径的圆,一直线
为直径的圆,一直线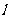 :
: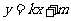 与⊙
与⊙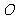 相切,与椭圆
相切,与椭圆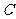 交于不同的两点
交于不同的两点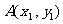 、
、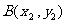 ,且满足
,且满足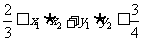 ,求
,求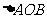 面积
面积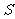 的最大值
的最大值
(13)已知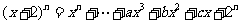 (
(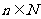 ,
,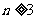 ),且
),且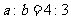 ,则
,则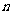 等于
等于
(14)设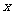 ,
,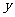 满足约束条件
满足约束条件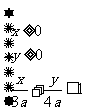 ,若目标函数
,若目标函数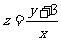 的最小值为1,则
的最小值为1,则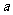 的值为
的值为
(15)已知定义在R上的奇函数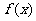 ,满足
,满足 ,且
,且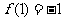 ,则
,则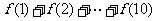 的值为
的值为
(16)正四棱柱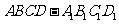 中,侧棱
中,侧棱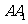 的长大于底面AB的长且顶点在同一个球面上,任意两个顶点的球面距离的最大值和最小值分别为
的长大于底面AB的长且顶点在同一个球面上,任意两个顶点的球面距离的最大值和最小值分别为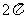 和
和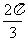 ,则正四棱柱
,则正四棱柱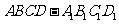 的体积为
的体积为
(1)已知集合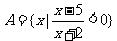 ,
,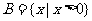 ,那么集合
,那么集合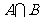 等于( )
等于( )
(A)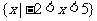 (B)
(B)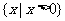
(C)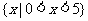 (D)
(D)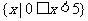
(2)已知圆的方程为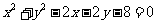 ,那么该圆的一条直径所在直线的方程为( )
,那么该圆的一条直径所在直线的方程为( )
(A)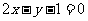 (B)
(B)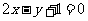
(C)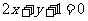 (D)
(D)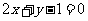
(3)已知函数 (
(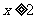 ),则其反函数
),则其反函数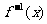 的定义域为( )
的定义域为( )
(A) (B)
(B)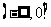 (C)
(C)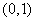 (D)
(D)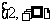
(4)下列所给的有关命题中,说法错误的命题是( )
(A)命题“若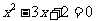 ,则
,则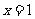 ”的逆否命题是“若
”的逆否命题是“若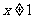 ,则
,则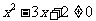 ”
”
(B)“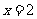 ”是“
”是“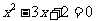 ”的充分不必要条件
”的充分不必要条件
(C)若 或
或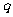 为假命题,则
为假命题,则 、
、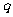 均为假命题
均为假命题
(D)若“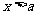 ”是“
”是“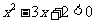 ”的必要不充分条件,则
”的必要不充分条件,则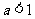
(5)在正四棱锥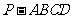 中,
中,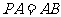 ,
,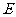 、
、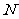 、
、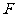 分别为棱
分别为棱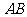 、棱
、棱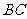 和棱
和棱 的中点,则异面直线
的中点,则异面直线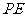 与
与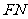 所成角为( )
所成角为( )
(A)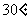 (B)
(B) (C)
(C)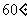 (D)
(D)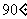
(6)已知抛物线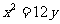 的准线过双曲线
的准线过双曲线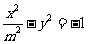 的一个焦点,则双曲线的离心率为( )
的一个焦点,则双曲线的离心率为( )
(A)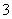 (B)
(B)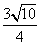 (C)
(C)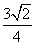 (D)
(D)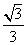
(7)已知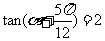 ,则
,则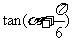 的值为( )
的值为( )
(A)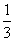 (B)1 (C)2 (D)3
(B)1 (C)2 (D)3
(8)已知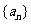 是等差数列,
是等差数列,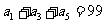 ,
,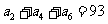 ,
,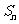 表示
表示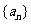 的前
的前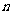 项和,则使
项和,则使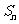 达到最大值的
达到最大值的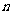 是( )
是( )
(A)18 (B)19 (C)20 (D)21
(9)2010年上海世博会期间,A、B、C、D四名志愿者分别从事翻译、导游、礼仪、司机四项工作,则A不从事翻译且B不从事导游的不同组合方案有( )
(A)6种 (B)8种 (C)14种 (D)24种
(10)已知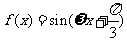 (
( )的图像与
)的图像与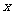 轴两相邻交点间的距离为
轴两相邻交点间的距离为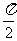 ,要得到
,要得到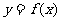 的图像只须把
的图像只须把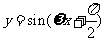 的图像( )
的图像( )
(A)向左平移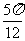 个单位 (B)向右平移
个单位 (B)向右平移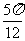 个单位
个单位
(C)向左平移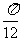 个单位 (D)向右平移
个单位 (D)向右平移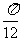 个单位
个单位
(11)在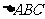 中,
中,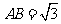 ,
,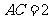 ,若
,若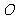 为
为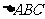 内部一点,且满足
内部一点,且满足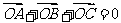 ,则
,则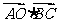 等于( )
等于( )
(A)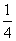 (B)
(B)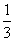 (C)
(C)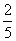 (D)
(D)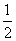
(12)已知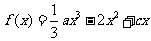 的导函数的值域为
的导函数的值域为 ,是
,是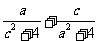 的最小值为( )
的最小值为( )
(A)0 (B)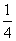 (C)
(C)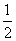 (D)1
(D)1
第Ⅱ卷
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com