
22.(本小题10分)口袋中有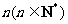 个白球,3个红球.依次从口袋中任取一球,如果取到红球,那么继续取球,且取出的红球不放回;如果取到白球,就停止取球.记取球的次数为X.若
个白球,3个红球.依次从口袋中任取一球,如果取到红球,那么继续取球,且取出的红球不放回;如果取到白球,就停止取球.记取球的次数为X.若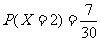 ,求:
,求:
(1)n的值;
(2)X的概率分布与数学期望.
21.[选做题]
A.选修4-1:几何证明选讲
如图,设AB为⊙O的任一条不与直线l垂直的直径,P是⊙O与l的公共点,AC⊥l,BD⊥l,垂足分别为C,D,且PC=PD,求证:
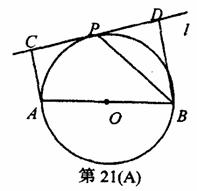 (1)l是⊙O的切线;
(1)l是⊙O的切线;
(2)PB平分∠ABD.
|
B.选修4-2:矩阵与变换
二阶矩阵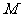 对应的变换将点
对应的变换将点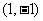 与
与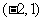 分别变换成点
分别变换成点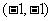 与
与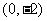 .求矩阵
.求矩阵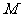 ;
;
C.选修4-4:坐标系与参数方程
若两条曲线的极坐标方程分别为r =l与r =2cos(θ+),它们相交于A,B两点,求线
段AB的长.
D.选修4-5:不等式选讲
求函数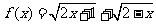 的最大值.
的最大值.
[必做题]
20.设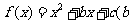 、
、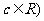 .
.
(1)若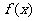 在
在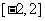 上不单调,求
上不单调,求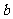 的取值范围;
的取值范围;
(2)若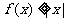 对一切
对一切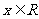 恒成立,求证:
恒成立,求证: ;
;
(3)若对一切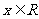 ,有
,有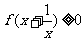 ,且
,且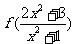 的最大值为1,求
的最大值为1,求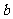 、
、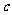 满足的条件.
满足的条件.
加试部分
19. 已知等比数列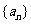 的前
的前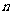 项和为
项和为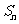 ,且点
,且点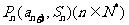 在函数
在函数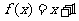 的图象上.
的图象上.
(1)求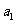 的值;
的值;
(2)若数列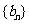 满足:
满足: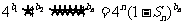 ,且
,且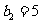 .求数列
.求数列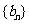 的通项公式.
的通项公式.
18.如图,已知圆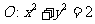 交
交 轴于
轴于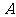 、
、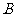 两点,
两点,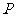 在圆
在圆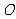 上运动(不与
上运动(不与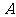 、
、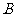 重合),过
重合),过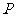 作直线
作直线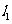 ,
,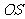 垂直于
垂直于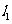 交直线
交直线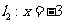 于点
于点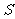 .
.
(1)求证:“如果直线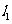 过点
过点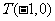 ,那么
,那么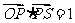 ”为真命题;
”为真命题;
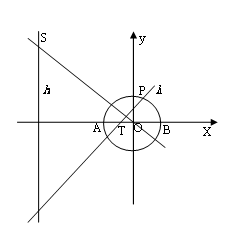 (2)写出(1)中命题的逆命题,判断它是真命题还是假命题,并说明理由.
(2)写出(1)中命题的逆命题,判断它是真命题还是假命题,并说明理由.
17. 如图,棱柱ABCD-A1B1C1D1的底面ABCD为菱形,平面AA1C1C⊥平面ABCD.
(1)证明:BD⊥AA1;
(2)证明:平面AB1C//平面DA1C1
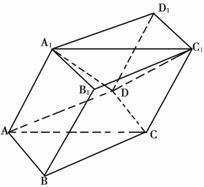 (3)在直线CC1上是否存在点P,使BP//平面DA1C1?若存在,求出点P的位置;若不存在,说明理由.
(3)在直线CC1上是否存在点P,使BP//平面DA1C1?若存在,求出点P的位置;若不存在,说明理由.
16. 已知向量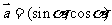 ,
, ,设函数
,设函数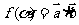 .
.
(1)求函数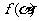 的最大值;
的最大值;
(2)在锐角三角形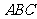 中,角
中,角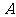 、
、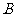 、
、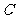 的对边分别为
的对边分别为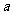 、
、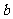 、
、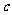 ,
,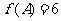 ,且
,且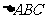 的面积为3,
的面积为3,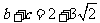 ,求
,求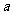 的值.
的值.
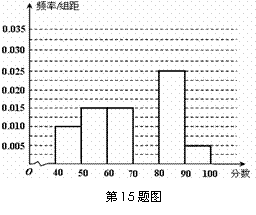
15.某校从参加高一年级期中考试的学生中随机抽取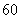 名学生,将其数学成绩(均为整数)
名学生,将其数学成绩(均为整数)
分成六段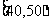 ,
,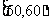 …
…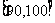 后得到如下部分频率分布直方图.观察图形的信息,
后得到如下部分频率分布直方图.观察图形的信息,
回答下列问题:
(Ⅰ)求分数在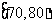 内的频率,并补全这个频率分布直方图;
内的频率,并补全这个频率分布直方图;
(Ⅱ)统计方法中,同一组数据常用该组区间的中点值作为代表,据此估计本次考试的平均分;
(Ⅲ)用分层抽样的方法在分数段为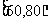 的学生中抽取一个容量为
的学生中抽取一个容量为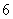 的样本,将该样本看成一个总体,从中任取
的样本,将该样本看成一个总体,从中任取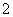 人,求至多有
人,求至多有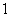 人在分数段
人在分数段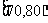 的概率.
的概率.
14. 已知连续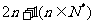 个正整数总和为
个正整数总和为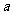 ,且这些数中后
,且这些数中后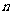 个数的平方和与前
个数的平方和与前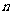 个数的平方和之差为
个数的平方和之差为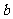 .若
.若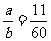 ,则
,则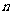 的值为 .
的值为 .
13. 已知函数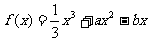 (
(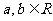 ),若
),若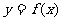 在区间
在区间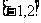 上是单调减函数,则
上是单调减函数,则 的最小值为 .
的最小值为 .
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com